Нижнетагильский технологический институт (филиал)

Стр 1 из 8Следующая ⇒

Нижнетагильский технологический институт (филиал)

Обобщенные позиционные задачи

Рекомендовано учебно-методическим советом

Нижнетагильского технологического института (филиал) УрФУ

имени первого Президента России Б.Н.Ельцина

в качестве учебно-методического пособия для выполнения РГР

по дисциплине

«Инженерная графика и компьютерная графика» для студентов всех форм обучения

всех направлений/специальностей подготовки

Нижний Тагил

2018

УДК 515(075.8)

ББК 22.15

Рецензенты:

доц. кафедры ЭЭТС УралЭНИН УрФУ, канд. техн. наук В. А. Дмитриевский

доц. кафедры ЭЭТС УралЭНИН УрФУ, канд. техн. наук В. А. Прахт

Научный редактор: проф.докт. техн. наук Е.Н.Сафонов

Обобщенные позиционные задачи.: учеб.-метод. пособие для выполнения расчетно- графической работы /авт.-сост. Л.Е.Аляутдинова; М-во образования и науки РФ; ФГАОУГОУ ВО «УрФУ им. первого Президента России Б.Н.Ельцина», Нижнетагил. технол. ин-т (фил.). – Нижний Тагил: НТИ (филиал) УрФУ, 2018. – с.73

Является составной частью учебно-методического обеспечения. Составлено с учетом требований образовательных стандартов. Содержит основные теоретические сведения и примеры решения задач по основным темам курса.

Библиогр.: 6 назв. Рис.27. Прил. 5.. Рис. П. 3

УДК 515(075.8)

ББК 22.15

Ó Аляутдинова Л.Е., составление, 2018

Оглавление

ВВЕДЕНИЕ……………………………………………………………………………….. принятые ОБОЗНАЧЕНИЯ…………………………………………………………. 1. ОСНОВНЫЕ ПОНЯТИЯ ОБ ОБОБЩЕННЫХ ПОЗИЦИОННЫХ ЗАДАЧАХ...………. 2. ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ ПРОЕЦИРУЮЩЕЙ ПЛОСКОСТЬЮ………………. Пересечение цилиндрической поверхности плоскостью………………………………… Пересечение конической поверхности плоскостью ……………………………………… Пересечение сферы плоскостью…………………………………………………………… Пересечение тора плоскостью ……………………………………………………………... 3. ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ ПРЯМОЙ ЛИНИЕЙ………………………… 4. ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ ………………………………………………………… Построение линии пересечения поверхностей, когда одна из них (или обе) является проецирующей………………………………………………………………………………. Построение линии пересечения поверхностей, когда ни одна из них не является проецирующей …….………………………………………………………………… Способ вспомогательных секущих плоскостей………………………………………… Способ вспомогательных секущих сфер…………………………………………………. Способ вспомогательных концентрических сфер ……………………………………….. Способ вспомогательных эксцентрических сфер………………………………………… Частные случаи пересечения поверхностей второго порядка 5. РАЗВЕРТКА КРИВЫХ ПОВЕРХНОСТЕЙ……………………………. Понятие развертки……………………………………………….. Основные свойства развертки…………………………………………………………… Построение развертки цилиндрической и конической поверхности……………….. Построение развертки методом аппроксимации Построение развертки прямого кругового цилиндра Построение развертки прямого кругового конуса Библиографический список………………………………………………………. ПРИЛОЖЕНИЯ 1. Содержание расчетно-графической работы………………………………………………. 2.Пример выполнения расчетно-графической работы……………………………………… 3. Варианты заданий к эпюру № 1……………………………………………… 4. Варианты заданий к эпюру № 2…………………………………………………… 5. Варианты индивидуальных заданий к эпюру №2а…………………………………

4 4 6 6 7 8 11 12 15 19 19 23 24 25 28 29 31 36 36 36 37 38 39 40 41 42 42 45 52 58 65

ВВЕДЕНИЕ

Данное учебно-методическое пособие соответствуют программе дисциплины «Инженерная и компьютерная графика» для всех направлений подготовки и всех форм обучения. Рекомендовано для выполнения РГР, подготовки к экзамену. В данном пособии показан процесс решения ряда типовых задач и предложены подобные задачи для самостоятельного решения. Для улучшения процесса решения некоторые задачи даны с наглядными изображениями. Даны примеры алгоритмов решения задач и анализы условий и полученных решений. В приложении приводятся варианты индивидуальных заданий для студентов по выполнению расчетно-графической работы, содержатся все необходимые сведения по ее выполнению и оформлению.

При выполнении любого чертежа должно быть соблюдено единство правил оформления. Чертеж должен выполняться на формате, размеры и форму которого определяет ГОСТ 2.301–68. Наиболее употребительны форматы А3(297× 420) и А2(420× 594)

В соответствии с ГОСТ 2.303–68, который определяет типы линий, их толщину и назначение, изображают чертеж задания. Все видимые основные линии – сплошные толщиной S = 0, 8–1, 0 мм. Остальные линии – толщиной от S/2 до S/3.

Текстовая часть чертежа, заполнение основной надписи (ГОСТ 2.104–68), цифры должны быть выполнены в соответствии с требованиями ГОСТ 2.304–81. Рекомендуемый размер шрифта высотой 3, 5 или 5 мм.

Размерные числа наносят над размерной линией приблизительно на расстоянии 0, 8...1 мм от нее. Подробные сведения о правилах оформления и выполнения чертежей содержатся в учебной и справочной литературе.

ПРИНЯТЫЕ ОБОЗНАЧЕНИЯ

Геометрические знаки

А, В, С, … – точки пространства;

a, b, c, … – обозначение точек и прямых на координатных плоскостях;

(АВ) – прямая, проходящая через точки А и В (заданная точками А и В);

[АВ] – отрезок прямой, ограниченный точками А и В;

|АВ| – расстояние между точками А и В (длина отрезка АВ);

H, V, W, … – обозначение плоскостей проекций;

(АВС) – плоскость, заданная точками А, В, С;

∠ ABC, ∠ B – обозначение угла;

|A, H| – расстояние от точки до плоскости;

∠ α – угол наклона заданной прямой или плоскости к горизонтальной плоскости проекций;

∠ β – угол наклона заданной прямой или плоскости к фронтальной плоскости проекций;

ОСНОВНЫЕ ПОНЯТИЯ ОБ ОБОБЩЕННЫХ ПОЗИЦИОННЫХ ЗАДАЧАХ

Под позиционными подразумеваются задачи, решение которых позволяет получить ответ о принадлежности элемента (точки) или подмножества (линии) множеству (поверхности) геометрическим фигурам.

Позиционные задачи занимают важное место в начертательной геометрии. Ранее мы рассматривали такие задачи, связанные с нахождением точки пересечения прямой линии с плоскостью и построением линии пересечения плоскостей. Теперь рассмотрим способы решения позиционных задач с участием кривых линий и поверхностей. Эти задачи называют обобщенными. Задачи с участием прямых линий и плоскостей являются их частными случаями. В общем же случае эти задачи формулируют так:

Построить точки пересечения:

1) плоскости с поверхностью

2) линии с поверхностью

3) поверхности с поверхностью

Задача.

По заданной фронтальной проекции сферы с вырезом построить горизонтальную и профильную проекции (рис. 3) .

Решение:

1. Анализ графического условия:

Вырез сферы выполнен плоскостями Р1 и Р2, которые пересекают сферу по окружности. Но эти плоскости перпендикулярными фронтальной плоскости проекций. Поэтому линии пересечения (окружности) на этой плоскости проекций на чертеже отражаются отрезками. Плоскость Р1 пересекая сферу по окружности, отображается на горизонтальной и профильной проекции в виде эллипса Фронтально-проецирующая плоскость Р2 является еще и профильной плоскостью уровня, то есть параллельна профильной плоскости проекций. Поэтому отображается на профильной плоскости проекций без искажения – в виде окружности.

2. Строим характерные точки, лежащие на экваторе –точка В, главном фронтальном меридиане –точки А и Е и главном профильной меридиане- точка С.

3. Строим случайные точки, используя параллели сферы (например, точку N). Соединяем построенные точки, устанавливая при этом видимость линий.

4. Очерк сферы на горизонтальной проекции определяет линия экватора от точки d до точки d и от точки b до точки b.

5. Очерк сферы на профильной проекции определяет линия главного профильного меридиана от точки с до точки с

Рис.3. Сфера с вырезом

Пересечение тора плоскостью

Тор-алгебраическая поверхность четвертого порядка. При пересечении тора плоскостью получаются плоские алгебраические кривые 4-го порядка, общее название которых – кривые Персея (в честь геометра Древней Греции). Вид кривых зависит от расстояния секущей плоскости до оси тора (рис. 4).

Кроме того, тор имеет три семейства окружностей:

Первое - секущие плоскости, проходят через ось тора. В сечении получаются две окружности – образующие тора (меридианы)

Второе - секущие плоскости проходят перпендикулярно оси вращения. В сечении получаются две окружности – параллели.

Третье –секущая плоскость качается двух окружностей главного меридиана смешанным образом. В сечении получаются две окружности –круги Вилларсо.

Рис. 4. Сечения тора – кривые Персея

Задача.

По заданной фронтальной проекции тора с вырезом построить его горизонтальную проекцию (рис. 5) .

Решение:

1. Анализ графического условия:

Вырез тора выполнен плоскостями Р 1 и Р 2. Плоскость Р1 пересекает тор по окружностям радиуса R A и R B. Эта плоскость перпендикулярна фронтальной плоскости проекций. Поэтому линии пересечения (окружности) на этой плоскости проекций на чертеже отражаются отрезками. Плоскость Р 1 пересекая тор по окружностям, отображается на горизонтальной в виде окружности, так как она является горизонтальной плоскостью уровня. Фронтально проецирующая плоскость Р 2 рассекает тор по кривой Персея, которая отображается на горизонтальной плоскости проекций с искажением

2. Строим характерные точки, лежащие на экваторе и на горле–точка D, главном фронтальном меридиане –точки А, В и N и главном профильной меридиане- точка С.

3. Строим случайные точки, используя параллели тора (например, точку 3). Соединяем построенные точки, устанавливая при этом видимость линий.

4. На горизонтальной проекции определяем очерк тора, оставшийся после выреза. Очерк тора на горизонтальной проекции определяется линией экватора. Линия экватора осталась после выреза от точки D с правой стороны оси вращения. Поэтому на горизонтальной проекции линия экватора определяется от точки d до точки d.

Рис. 5. Построение тора с вырезом

Задача.

Определить точки пересечения прямой общего положения АВ с заданной поверхностью (рис.6).

Решение:

1. Анализ графического условия задачи:

Заданы прямая АВ общего положения и самопересекающийся тор.

Любая плоскость, проходящая через прямую АВ, пересечет тор по кривой 4-го порядка.

2. Проводим через прямую АВ фронтально-проецирующую Р (след Р _V). Фронтальная проекция линии пересечения этой плоскости с поверхностью тора отобразится отрезком 1–7 на следе Р _V.

3. Строим линию пересечения проведенной плоскости и заданной поверхности. Горизонтальную проекцию линии пересечения строим по множеству точек, исходя из условия принадлежности поверхности тора, проводя через точки параллели определенного радиуса

4. Искомые точки определяем в пересечении данной прямой с построенной фигурой сечения – точки С и D.

5. Определяем видимость прямой АВ относительно поверхности тора

Рис. 6. Определение точек пересечения прямой с поверхностью тора

Определение искомых точек значительно упрощается, если поверхность или прямая занимают проецирующее положение.

Задача.

Определить точки пересечения прямой АВ с поверхностью кругового цилиндра (рис.7, а).

а б

Рис.7. Определение точек пересечения прямой линии

и кривой поверхности при проецирующем положении:

а) поверхности; б) прямой линии

Решение:

Так как цилиндр занимает горизонтально-проецирующее положение, то горизонтальные проекции искомых точек m и n расположены на горизонтальном следе поверхности (окружности). Фронтальные проекции точек определяем, исходя из условия принадлежности их данной прямой.

Задача.

Определить точки пересечения сферы с фронтально-проецирующей прямой АВ (рис.7, б).

Решение:

Так как прямая занимает положение, перпендикулярное плоскости V, то фронтальные проекции искомых точек m' и n' совпадут с фронтальной проекцией самой прямой. Горизонтальные проекции точек m и n находим из условия принадлежности их сфере при помощи соответствующих параллелей.

Задача.

Определить точки пересечения прямой общего положения АВ с поверхностью пирамиды (рис. 8).

Рис. 8. Определение точек пересечения прямой с поверхностью пирамиды

Решение:

1. Через прямую MN фронтально проецирующую плоскость Р (след Р V)

2. Строим сечение пирамиды и проведенной плоскости Р

3. Находим искомые точки D и Е как точки пересечения построенного сечения и заданной прямой

4. Определяем видимость прямой MN относительно пирамиды

ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ

В результате решения таких позиционных задач определяется линия пересечения поверхностей, все точки которой одновременно принадлежат обеим поверхностям. Порядок линии пересечения алгебраических поверхностей равен произведению порядков этих поверхностей.

Построение линии пересечения поверхностей является наиболее распространенной задачей в инженерной практике. Рассмотрим способы их построения, которые встречаются наиболее часто.

Решение задачи всегда начинают с анализа условия, выясняя: какие поверхности пересекаются; какое положение они занимают относительно плоскостей проекций и друг друга; какие линии должны получиться в пересечении поверхностей (плоские, пространственные, характер проекций линии). После этого выбирают рациональный способ решения.

При построении точек линии пересечения поверхностей при любом способе вначале находят те точки, которые называют характерными или опорными:

– принадлежащие очеркам данных поверхностей;

– наиболее удаленные на экстремальное расстояние (min и max) от плоскостей проекций – ближняя и дальняя; высшая и низшая; крайняя левая и правая;

– определяющие границы видимости проекций кривой.

Затем находят промежуточные точки искомой линии.

Построенные точки соединяют между собой, учитывая характер линии пересечения и ее проекций. Следует иметь в виду, что проекции линии пересечения поверхностей должны всегда быть в пределах контура наложения проекций этих поверхностей.

Определяют видимость проекций линии пересечения и взаимную видимость поверхностей.

Построение линии пересечения поверхностей,

когда одна из них (или обе) является проецирующей

К проецирующим поверхностям относят плоскости частного положения или цилиндрические поверхности, образующие которых перпендикулярны какой-либо плоскости проекций. Они обладают свойством: все точки, принадлежащие им, проецируются на их следы. Значит одна из проекций (или две) линии пересечения известна – она совпадает со следом проецирующей поверхности.

Задача.

Построить линию пересечения цилиндров вращения

Решение:

1. Анализ графического условия задачи: у пересекающихся цилиндров (рис. 9) поверхности являются проецирующими: горизонтально проецирующей и профильно проецирующей. Линия пересечения будет представлять пространственную кривую 4-го порядка. Горизонтальная проекция отобразится на след горизонтально-проецирующего цилиндра (окружность), а профильная – на след профильно-проецирующего цилиндра.

2. Т. к. поверхности имеют общую фронтальную плоскость симметрии, их фронтальная проекция будет представлять гиперболу (две конкурирующие ветви), которую строим по общему правилу построения кривой линии по точкам, когда две проекции точек известны.

Рис. 9. Пересечение двух проецирующих цилиндров

Задача.

Построить линию пересечения заданных поверхностей (рис.10)

Решение:

1. Анализ графического решения задачи. Заданы цилиндр и конус вращения. Цилиндр занимает фронтально проецирующее положение. Линия пересечения – кривая 4-го порядка. Фронтальная проекция – окружность – совпадает с фронтальным следом цилиндрической поверхности. Горизонтальную и профильную проекции линии пересечения строим по множеству точек, исходя из условия их принадлежности непроецирующей поверхности (в данном случае конической), используя ее параллели.

2. Начинаем построение с характерных точек: 1, 2, 3, 4, 5, 6. Точки 1 и 6 принадлежат фронтальной образующей конуса; 3 – горизонтальной образующей цилиндра; 2 и 4 – профильным образующим конуса; 5 – профильной образующей цилиндра.

Точка К – одна из промежуточных точек.

3. Построенные горизонтальные и профильные проекции точек соединяем плавными кривыми, устанавливая при этом их видимость и видимость образующих поверхностей.

Рис. 10. Построение линии пересечения конуса

с проецирующим цилиндром

Задача. Построить линию пересечения сфера и цилиндра вращения (рис.11)

Решение:

1. Анализ графического решения задачи:

Цилиндрическая поверхность – фронтально проецирующая, следовательно, фронтальная проекция линии пересечения отображается на ее след (окружность).

2. Все обозначенные точки, кроме К, являются характерными. Данные поверхности имеют общую фронтально-проецирующую плоскость симметрии Р (след Р _V), в которой находятся точки 1 и 6. Точка 1 принадлежит главному фронтальному меридиану сферы, две точки 6 – самая ближняя и дальняя точки линии пересечения. Точки 7 и 3 принадлежат экватору сферы. Точки 2 и 8, принадлежащие горизонтальным образующим цилиндра, являются граничными для горизонтальной проекции линии пересечения. Точки 5 и 9, принадлежащие профильному меридиану сферы, являются граничными для профильной проекции линии пересечения. Точки 4 и 10 принадлежат профильным образующим цилиндра.

Рис. 11. Построение линии пересечения сферы и цилиндра

а-на эпюре Монжа, б-пространственная модель (начало- окончание на стр.23)

Рис. 11. Построение линии пересечения сферы и цилиндра

а-на эпюре Монжа, б-пространственная модель (окончание-начало на стр.22)

Построение линии пересечения поверхностей, когда

ни одна из поверхностей не является проецирующей

В этом случае применяют общий способ построения линии пересечения, который заключается в использовании вспомогательных секущих поверхностей-посредников.

Сформулируем общее правило построения линии пересечения поверхностей:

1) выбрать вид вспомогательных поверхностей;

2) построить линии пересечения вспомогательных поверхностей с заданными поверхностями;

3) найти точки пересечения построенных линий и соединить их между собой плавной кривой.

В качестве вспомогательных поверхностей выбирают такие, линии пересечения которых с заданными поверхностями проецируются на чертеж в графически простые линии – прямые, окружности. В качестве вспомогательных поверхностей можно, например, использовать плоскости или сферы. Рассмотрим их применение.

Задача.

Построить линию пересечения конуса вращения со сферой. (рис. 12).

Решение:

1. Анализ графического условия:

Для построения линии пересечения заданных поверхностей удобно в качестве вспомогательных поверхностей использовать серию горизонтальных плоскостей, перпендикулярных оси конуса, которые пересекают сферу и конус по окружностям. На пересечении этих окружностей находят точки искомой линии пересечения.

2. Построение начинают с определения характерных точек. Так как поверхности имеют общую фронтальную плоскость симметрии, то в пересечении их главных фронтальных меридианов находится высшая а и низшая b точки линии пересечения. Определение этих точек дает возможность установить предел проведения вспомогательных плоскостей.

3. Точка С, лежащая на экваторе сферы, находят при помощи горизонтальной плоскости P 1, пересекающей сферу по экватору и конус по окружности радиуса R_c В пересечении горизонтальных проекций этих окружностей определяют искомые точки, которые устанавливают границы видимости горизонтальной проекции линии пересечения.

4. Промежуточные точки находят при помощи случайных горизонтальных плоскостей, которые берут в установленном диапазоне. Они позволяют уточнить характер кривой линии.

5. Построенную горизонтальную проекцию точек соединяем плавной кривой, устанавливая при этом ее видимость

6. Определяем взаимную видимость образующих поверхностей

Рис. 12. Построение линии пересечения сферической и конической поверхностей способом секущих плоскостей

Способ вспомогательных сфер

Способ, в котором в качестве вспомогательных поверхностей используются сферы, основан на лемме о соосных поверхностях вращения.

Соосными называются поверхности, имеющие общую ось.

Лемма о соосных поверхностях вращения

Лемма. Соосные поверхности вращения пересекаются по окружностям столько раз, сколько раз пересекаются их главные меридианы

На рис. 13 показано пересечение соосных поверхностей, где

m –образующая первой поверхности вращения

n – образующая второй поверхности вращения

I –ось вращения поверхности m

Т – ось вращения поверхности п

Рис. 13. Пересечение соосных поверхностей вращения

За ось сферы можно принять любой ее диаметр. Если ось поверхности вращения проходит через центр сферы, то линия пересечения сферы и поверхности вращения – окружность, плоскость которой перпендикулярна оси поверхности вращения. При этом если ось поверхности вращения параллельна плоскости проекций, то линия пересечения на эту плоскость будет проецироваться отрезком прямой линии.

На рис. 14 показана фронтальная проекция пересечения сферой радиуса R поверхностей вращения – конуса, тора, цилиндра, сферы, оси которых проходят через центр сферы и параллельны плоскости V. Окружности, по которым пересекаются указанные поверхности вращения с поверхностью сферы, проецируются на плоскость V виде отрезков прямых.

Рис. 14. Пересечение соосных поверхностей вращения со сферой

Рис. 15. Пересечение соосных конусов вращения

На рис.15 показано пересечение соосных конусов вращения, имеющих общую фронтальную плоскость симметрии. Они пересекаются по окружности

Задача.

Построить линию пересечения заданных поверхностей (рис. 22)

Решение:

1. Анализ графического условия: заданые поверхности вращения конус и цилиндр имеют общую фронтальную плоскость симметрии. В обе поверхности вписана сфера. Поэтому линия персечения на фронтальной

проекции распадается на две плоские кривые второго порядка - два эллипса.

2. Горизонтальную проекцию линию персечения находим из принадлежности к поверхности конуса, привязывая точки параллелями.

3. Соединяем точки персечения плавной кривой, определяя ее видимость.

4. Определяем взаимную видимость поверхностей

Рис. 23. Поверхности, описанные вокруг одной сферы. Построение

линии пересечения поверхностей

5. Развертки кривых поверхностей

Понятие развертки

Если поверхность рассматривать как тонкую, нерастяжимую пленку, то некоторые поверхности путем изгибания могут быть совмещены с плоскостью. Такой процесс совмещения поверхности с плоскостью называется развертыванием поверхности. Поверхность, которая может быть совмещена с плоскостью без разрывов и складок, называется развертывающейся, а полученная при этом плоская фигура – ее разверткой.

Построение разверток многогранных поверхностей рассматривалось в предыдущей лекции. Такие развертки называются точными.

К развертывающимся кривым поверхностям относятся только линейчатые поверхности с пересекающимися смежными образующими: конические, цилиндрические и поверхности с ребром возврата. Развертки таких поверхностей называют приближенными. Развертки неразвертывающихся поверхностей (сфера, тор и т. д.) являются условными.

Основные свойства развертки

Поверхность и ее развертку можно рассматривать как точечные множества, между которыми установлено взаимно однозначное соответствие. Отсюда можно отметить основные свойства развертки:

1) длины соответствующих линий на поверхности и на развертке равны между собой;

2) прямой линии на поверхности соответствует прямая линия на развертке;

3) угол между линиями на поверхности равен углу между соответствующими линиями на развертке;

4) параллельным прямым линиям на поверхности соответствуют параллельные прямые линии на развертке;

5) площадь, ограниченная линией на поверхности, равна площади, ограниченной соответствующей ей линией, на развертке.

Чтобы на развертке построить какую-либо точку, принадлежащую развертываемой поверхности, необходимо предварительно через заданную точку на поверхности провести линию. Затем эту линию нанести на развертку, и на ней отметить точку.

Конических поверхностей

Развертка поверхности кругового цилиндра и конуса известны из школьного курса. Развертка поверхности кругового цилиндра (рис.24) представляет прямоугольник, одна сторона которого равна высоте цилиндра Н, а другая – длине окружности основания цилиндра

l =2π R,

где R – радиус окружности основания цилиндра.

Положение точки А на развертке цилиндрической поверхности найдено с помощью образующей, проходящей через нее. Отрезок прямой А1 на развертке равен длине дуги а1 окружности основания цилиндра, т. е.

l ₁ = 2π R φ ^о/ 360^о.

Рис. 24. Развертка поверхности прямого кругового цилиндра

Развертка поверхности кругового конуса (рис.10.2) представляет круговой сектор, радиус которого равен длине образующей конуса, а угол при вершине равен

a^о = 360^о R / L,

где R – радиус окружности основания конуса;

L – длина образующей этого конуса (рис. 25).

Положение точки А на развертке конуса найдено с помощью образующей S 2, проведенной через нее на поверхности конуса. Угол a₁ на развертке определяется по формуле

a^о₁ = a^оφ ^о/ 360^о.

Натуральная величина отрезка образующей SA определена вращением его вокруг оси конуса до положения, параллельного фронтальной плоскости проекций.

Рис. 25. Развертка поверхности прямого кругового конуса

Но такие способы построения разверток ограничены.

Библиографический список

1. Белякова Е. И. Начертательная геометрия: практикум: учеб. пособие для вузов / Е. И. Белякова, П. В. Зеленый; под ред. П. В. Зеленого. – 2-е изд., испр. – Минск: Новое знание; Москва: ИНФРА-М, 2012. - 214, [10] с.: ил.

2. Дегтярев, В. М. Инженерная и компьютерная графика: учебник для студентов вузов / В. М. Дегтярев, В. П. Затыльникова. – М.: Академия, 2010. - 240 с. – (Высшее профессиональное образование).

3. Левицкий В. С. Машиностроительное черчение и автоматизация выполнения чертежей: учебник для втузов / В. С. Левицкий. – 8-е изд., перераб. и доп. – М.: Высш. школа, 2007. – 435 с.: ил.

4.Нартова Л. Г. Начертательная геометрия: учебник для вузов / Л. Г. Нартова, В. И. Якунин. – 3-е изд., стер. – Москва: Академия, 2011. – 192 с.: ил.

5. Чекмарев А. А. Начертательная геометрия и черчение: учеб. для бакалавров / А. А. Чекмарев. – М.: Юрайт, 2012. – 472 с

6. Чекмарев А. А. Начертательная геометрия и черчение: учеб. для вузов / А. А. Чекмарев. – 2-е изд., перераб. и доп. – М.: ВЛАДОС, 2005. – 472 с

ПРИЛОЖЕНИЯ

ПРИЛОЖЕНИЕ 1

СОДЕРЖАНИЕ РАСЧЕТНО-ГРАФИЧЕСКОЙ РАБОТЫ

ЭПЮР №1

Задание

Построить линию пересечения заданной комплексной поверхности плоскостью Р. Найти натуральную фигуру сечения заданной поверхности и плоскости Р

ЭПЮР №2

Задание

Построить три ортогональных проекции линии пересечения заданных поверхностей. Выполнить развертку указанной поверхности Р с нанесением линии пересечения

ЭПЮР №2А

Задание

Построить две ортогональных проекции линии пересечения заданных поверхностей. Выполнить развертку указанной поверхности Р с нанесением линии пересечения

Эпюры выполняются на формате А3 в М1: 1 по вариантам из приложения №2. Форма основной надписи –1. Для правильного графического исполнения эпюра необходимо изучить ГОСТ:

ГОСТ 2.301- 68 –Форматы, ГОСТ 2.302- Масштабы, ГОСТ 2.303-68 –Линии, ГОСТ 2.304-81–Шрифты чертежные.

В правом нижнем углу чертежа выполняется основная надпись. Правила ее заполнения предусматривает ГОСТ 2.104–68.

Рис. П. 1. Форма 1 основной надписи

Для правильного графического исполнения эпюра необходимо изучить ГОСТы:

ГОСТ 2.301–68 – Форматы, ГОСТ 2.302–68 – Масштабы, ГОСТ 2.303–68 – Линии, ГОСТ 2.304–81 – Шрифты чертежные.

При выполнении любого чертежа должно быть соблюдено единство правил оформления.

В соответствии с ГОСТ 2.303–68, который определяет типы линий, их толщину и назначение, изображают чертеж задания. Все видимые основные линии – сплошные основные толщиной S = 0, 8–1, 0 мм, линии построений и линии связи – толщиной от S/2 до S/3.

2. Оформление основной надписи

В графе 1 записывается наименование изделия или документа (в именительном падеже, единственном числе, без переноса части слова на другую строку). В наименованиях, состоящих из нескольких слов, должен быть прямой порядок слов, например: «Эпюр № 3».

В графе 2 – обозначение документа, которое для всех тем составляется по типу:

ЭиЭ 003 029, где ЭиЭ – название специальности, 3 – № выполняемой работы, 29 – номер варианта.

Графа 3 – обозначение материала детали (графа заполняется только на чертежах деталей), например: Сталь 20 ГОСТ 1050–88.

Графа 4 – литера, присвоенная данному документу: ДР – домашняя работа; У – учебный чертеж.

Графа 6 – масштаб.

Графа 7 – порядковый номер листа (на документах, состоящих из одного листа, графу не заполняют).

Графа 8 – общее количество листов документа (графу заполняют только на первом листе).

Графа 9 – НТИ (филиал) УрФУ, номер группы и индекс специальности, например: гр. 140000.

Графа 10 – характер работы, выполняемой лицом, подписавшим чертеж (разработал, проверил или утвердил).

Графа 11 – фамилии лиц, подписавших чертеж.

Графа 12 – подписи лиц, фамилии которых указаны в гр. 11.

Графа 13 – даты, когда были сделаны подписи.

Пример заполнения основной надписи представлен на рис. П. 2.

Основная надпись заполняется шрифтом тип Б с наклоном. Графа 1 и 2 заполняются шрифтом № 10, остальные графы – шрифтом № 3, 5.

Рис. П. 2. Пример выполнения основной надписи

ПРИЛОЖЕНИЕ 2

Пример выполнения РГР

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное автономное образовательное учреждение

высшего образования

«Уральский федеральный университет имени первого Президента России Б.Н.Ельцина»

Нижнетагильский технологический институт (филиал)

Депортамент ЕНО

Дисциплина:

Инженерная и компьютерная графика

ВАРИАНТ №

ГРУППА

СТУДЕНТ

ПРЕПОДАВАТЕЛЬ

Нижний Тагил

201…

Рис.П1.Пример графического решения эпюра №1

Рис.П2.Пример графического решения эпюра №2

Рис..П3.Пример графического решения эпюра №2а

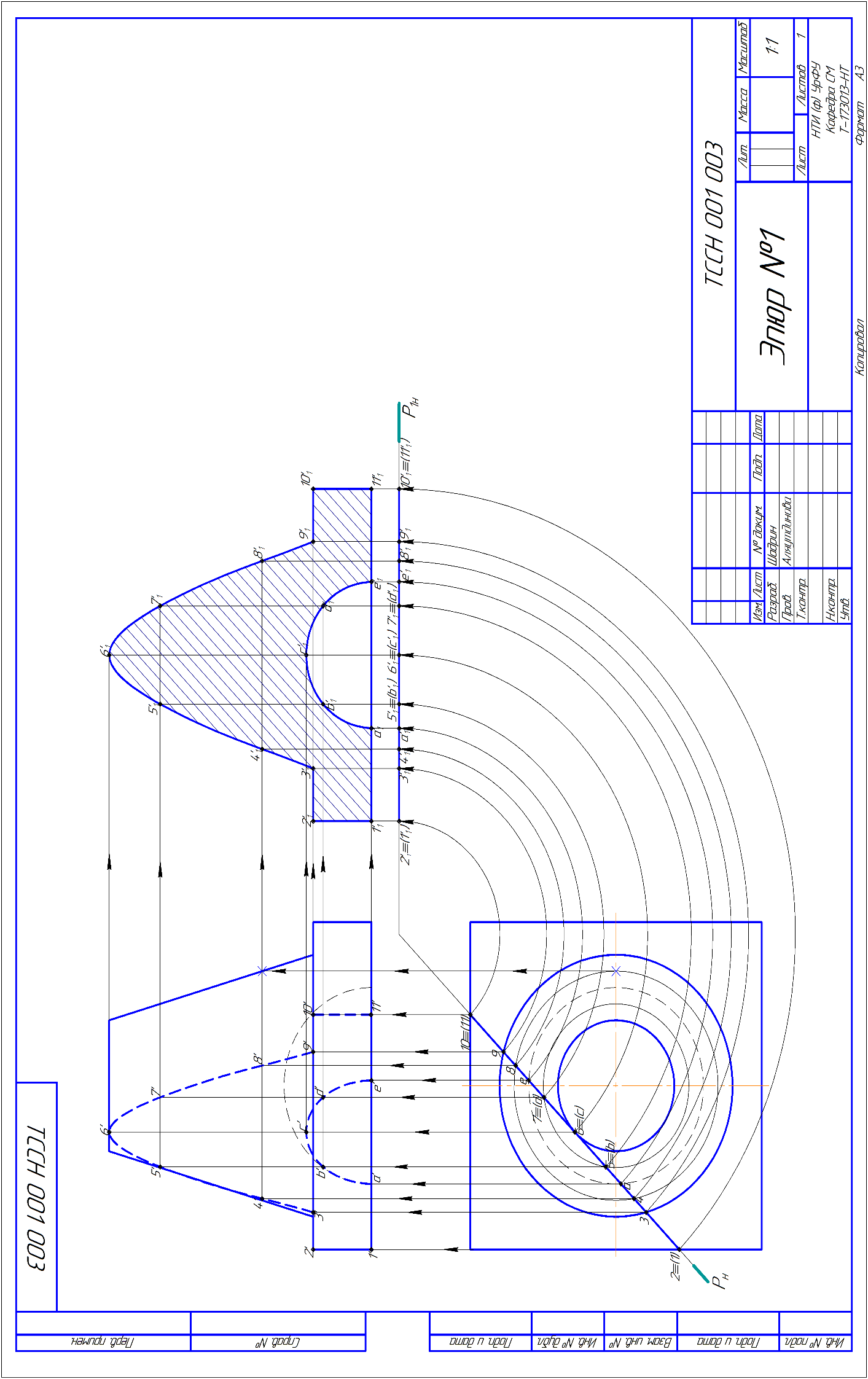
Эпюр №1.

Ход решения:

1. Анализируем графическое условие эпюра:

Комплексная поверхность состоит из усеченного конуса, прямой призмы и полусферы. Секущая плоскость Р занимает горизонтально проецирующее положение. Ожидаемая линия пересечения плоскости Р: с конусом – гипербола, с призмой- прямоугольник, со полусферой – полуокружность

2. Строим фронтальную линию пересечения заданной поверхности с плоскостью Р, исходя из принадлежности точек заданной поверхности

3. На горизонтальной плоскости проекций плоскости Р отмечаем точки: начальные и конечные –1 и 11, точки на поверхности конуса «привязываем» окружностями – параллелями, точки на поверхности сферы также «привязываем» окружностями.

4. Определяем видимость построенной линии пересечения

5. Для определения натуральной величины полученного сечения необходимо чертеж преобразовать так, чтобы заданная горизонтально проецирующая плоскость Р стала фронтальной плоскостью уровня.

6. В данной задаче натуральная величина построенного сечения найдена методом вращения плоскости Р вокруг проецирующей прямой. В данном случае – горизонтально проецирующей. На горизонтальной проекции каждая точка сечения совершает вращательное движение. На фронтальной - поступательное движение, параллельное оси Х.

7. Плоскость сечения Р стала занимать положение фронтальной плоскости уровня.

7. Новая фронтальная проекция сечения отображается в натуральную величину.

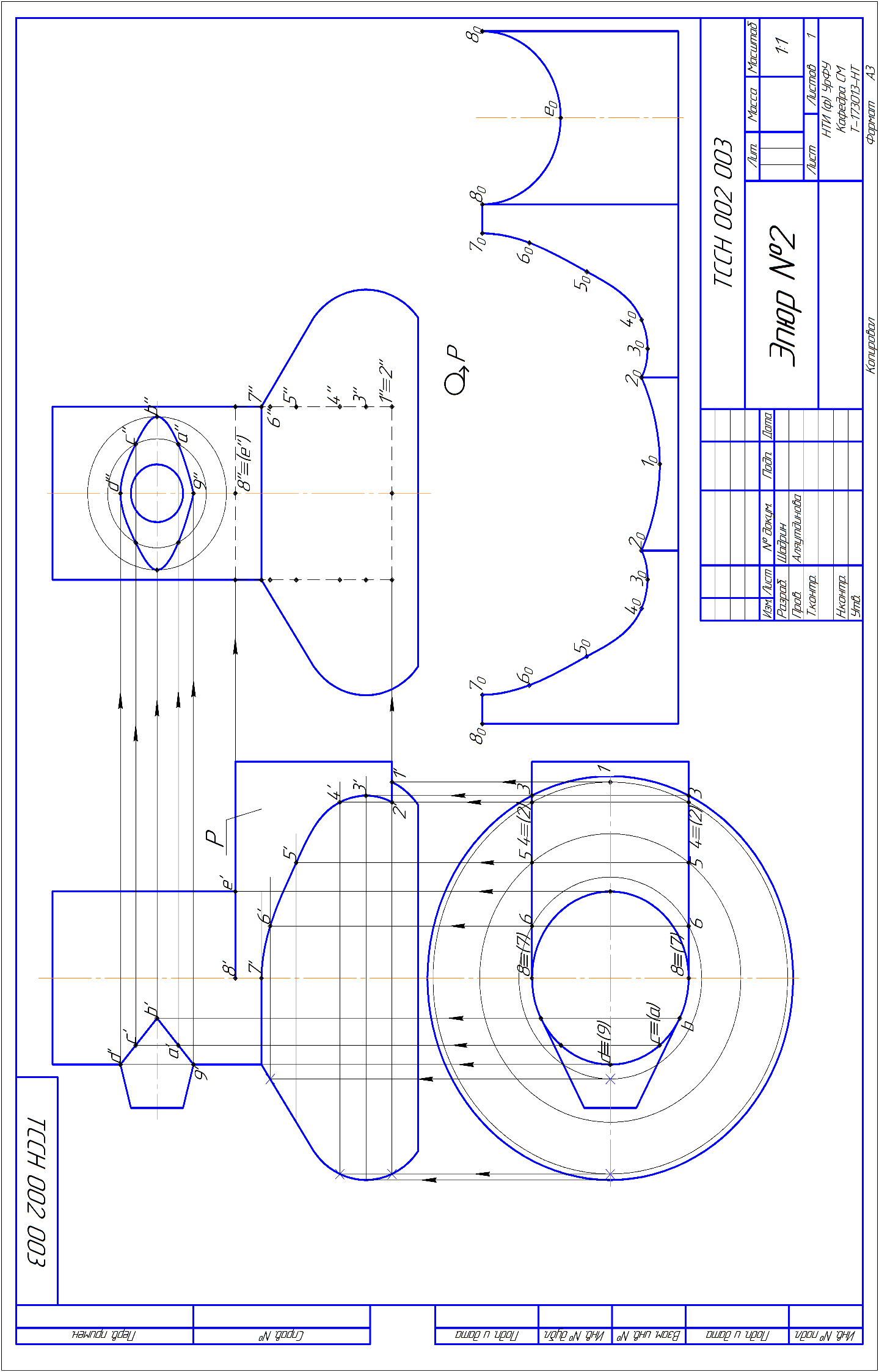
Эпюр №2.

Ход решения:

1. Анализируем графическое условие эпюра:

Комплексная поверхность состоит из усеченного конуса, прямого кругового цилиндра, прямой призмы, усеченного конуса и тора. Цилиндр занимает горизонтально проецирующее положение, призма – профильно проецирующее положение. Следовательно, линия пересечения будет строится из условия, что одна из пересекающихся поверхностей занимает проецирующее положение.

2. Строим линию пересечения горизонтально проецирующего цилиндра и усеченного конуса. Согласно условию, в цилиндр и конус можно вписать сферу, диаметр которой равен диаметру цилиндра. Применяем теорему Монжа, согласно которой, если две поверхности второго порядка описаны около третьей поверхности второго порядка или вписаны в нее, то линия их пересечения распадается на две кривые второго порядка, плоскости которых проходят через прямую, соединяющую точки пересечения линий касания. Поэтому на фронтальной проекции плоскости линии пересечения будут фронтально проецирующими. Все точки линии пересечения отображаются в виде прямых линий. Профильная проекция линии пересечения находится из принадлежности точек усеченному конусу.

3. Строим линию пересечения профильно проецирующей призмы с конусом и тором. Начинаем построение с горизонтальной проекции. Две боковые грани призмы являются фронтальными плоскостями уровня. На горизонтальной проекции они отображаются в виде прямых. Линия пересечения этих плоскостей с поверхностью конуса и тора совпадает с этими прямыми. Отмечаем на этих плоскостях точки. Фронтальную проекцию линии пересечения находим, привязывая точки к поверхности конуса и тора окружностями. Еще две боковые грани призмы являются горизонтальными плоскостями уровня. Нижняя грань призмы разрезает тор по окружности, верхняя разрезает цилиндр по окружности. Профильная проекция построенных линий пересечения совпадает с очерком призмы

4. Развертку призмы строим методом нормального сечения. Так как призма занимает профильно проецирующее положение, то боковые ребра призмы на фронтальной и горизонтальной проекции отображаются в натуральную величину. Поэтому линия пересечения переносится на развертку без дополнительных построений, так как на фронтальной проекции она отображена без искажения.

Эпюр №2А.

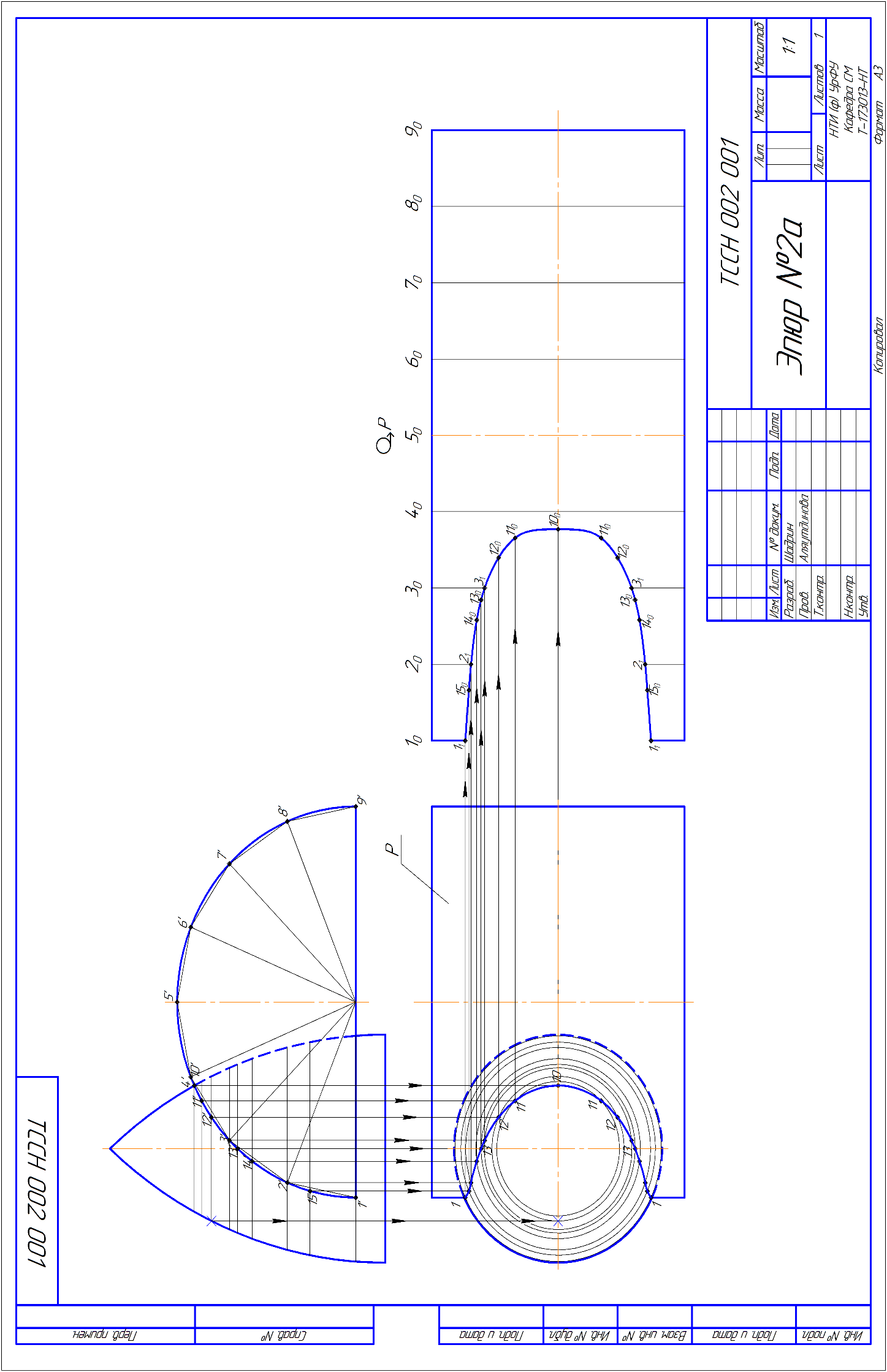
Ход решения:

1. Анализируем графическое условие эпюра:

Даны самопересекающийся тор и цилиндр. Ось вращения тора- горизонтально проецирующая прямая. Ось вращения цилиндра- фронтально проецирующая прямая. Следовательно, цилиндр – фронтально проецирующая поверхность. Линия пересечения заданных поверхностей будет строится из условия, что одна из пересекающихся поверхностей занимает проецирующее положение.

2.На фронтальной проекции линия пересечения совпадает с очерком цилиндра- окружностью.

3. Горизонтальную проекцию линии пересечения строим, привязывая точки к поверхности тора параллелями –окружностями

4. Строим пересечения тора с плоскостью, ограничивающий цилиндр на фронтальной проекции. Плоскость занимает положение горизонтальной плоскости уровня и разрезает тор по окружности.

5. На горизонтальной проекции эта окружность отображается без искажения.

6. Развертку цилиндрической поверхности строим методом аппроксимации – вписываем в цилиндр правильную призму. Число граней-16

7. Делим на фронтальной проекции полуокружность цилиндра на 8 равных частей.

8. Все точки линии пересечения переносим на развертку с горизонтальной проекции, так как образующие цилиндра отображаются на ней без искажения

ПРИЛОЖЕНИЕ 3

Варианты заданий к эпюру 1