РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА №1

⇐ ПредыдущаяСтр 8 из 8

ВАРИАНТ №

ГРУППА

СТУДЕНТ

ПРЕПОДАВАТЕЛЬ

Нижний Тагил

201…

Рис.П1.Пример графического решения эпюра №1

Рис.П2.Пример графического решения эпюра №2

Рис..П3.Пример графического решения эпюра №2а

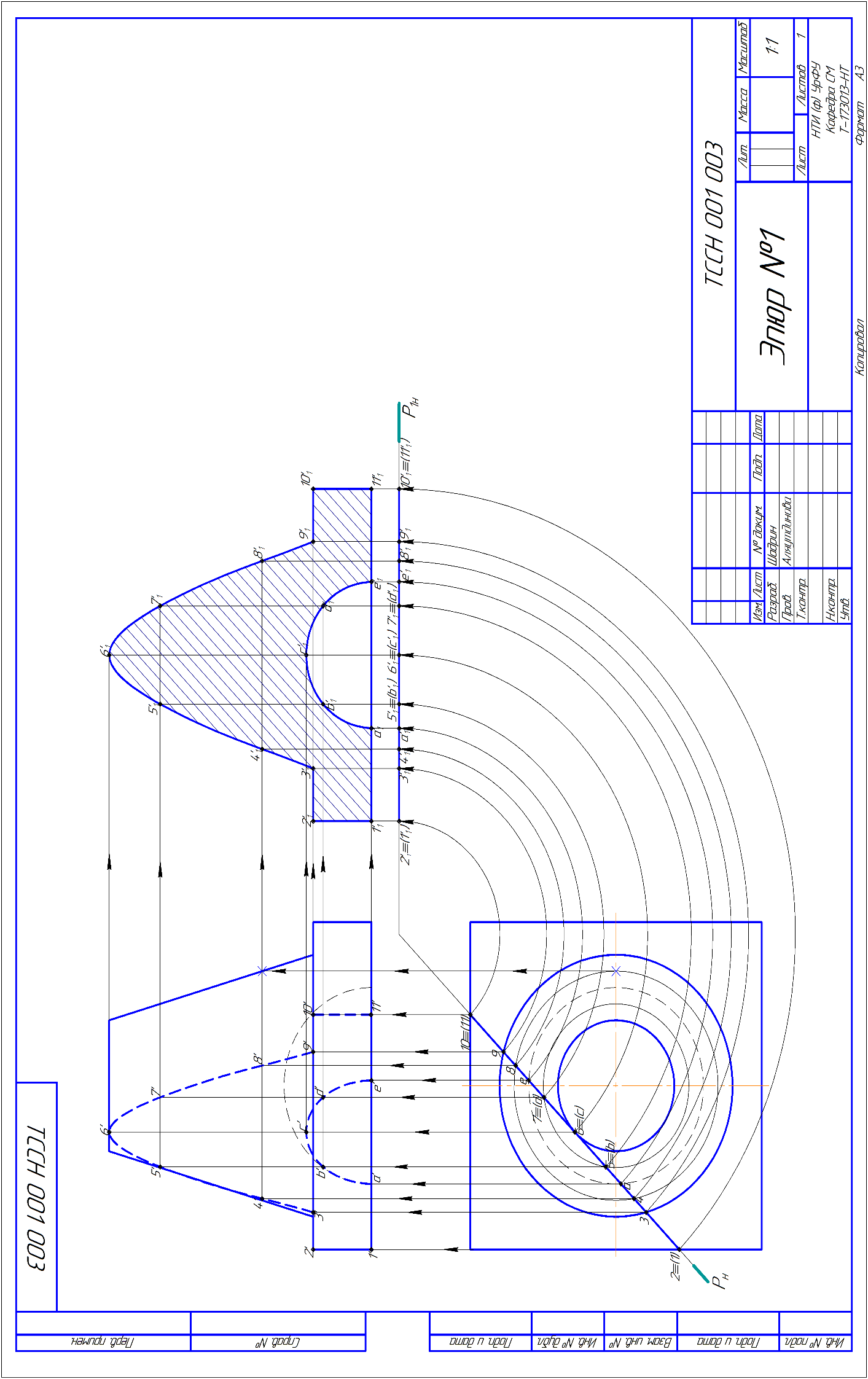
Расчетно -пояснительная записка к выполнению эпюров

Эпюр №1.

Ход решения:

1. Анализируем графическое условие эпюра:

Комплексная поверхность состоит из усеченного конуса, прямой призмы и полусферы. Секущая плоскость Р занимает горизонтально проецирующее положение. Ожидаемая линия пересечения плоскости Р: с конусом – гипербола, с призмой- прямоугольник, со полусферой – полуокружность

2. Строим фронтальную линию пересечения заданной поверхности с плоскостью Р, исходя из принадлежности точек заданной поверхности

3. На горизонтальной плоскости проекций плоскости Р отмечаем точки: начальные и конечные –1 и 11, точки на поверхности конуса «привязываем» окружностями – параллелями, точки на поверхности сферы также «привязываем» окружностями.

4. Определяем видимость построенной линии пересечения

5. Для определения натуральной величины полученного сечения необходимо чертеж преобразовать так, чтобы заданная горизонтально проецирующая плоскость Р стала фронтальной плоскостью уровня.

6. В данной задаче натуральная величина построенного сечения найдена методом вращения плоскости Р вокруг проецирующей прямой. В данном случае – горизонтально проецирующей. На горизонтальной проекции каждая точка сечения совершает вращательное движение. На фронтальной - поступательное движение, параллельное оси Х.

7. Плоскость сечения Р стала занимать положение фронтальной плоскости уровня.

7. Новая фронтальная проекция сечения отображается в натуральную величину.

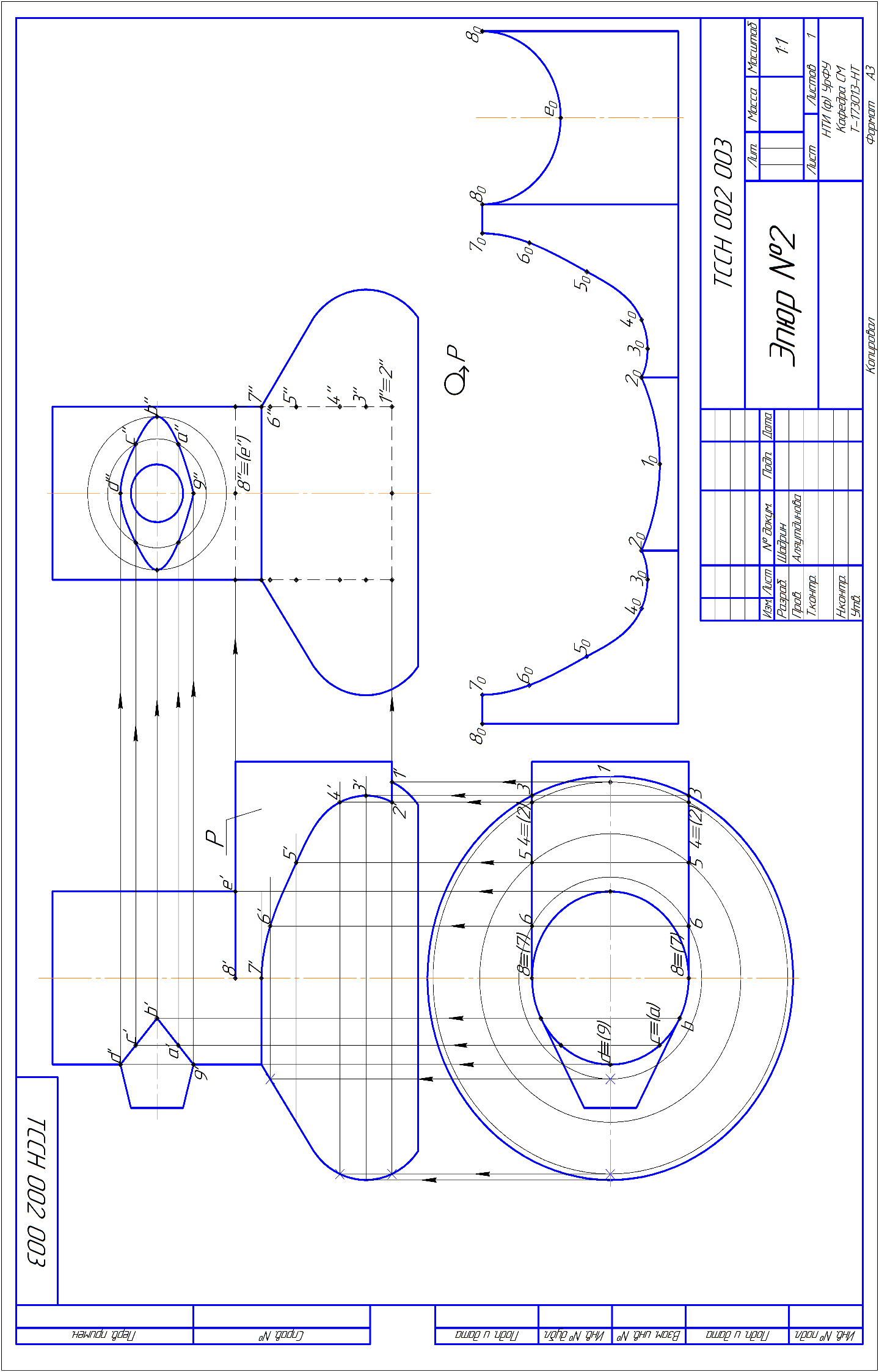
Эпюр №2.

Ход решения:

1. Анализируем графическое условие эпюра:

Комплексная поверхность состоит из усеченного конуса, прямого кругового цилиндра, прямой призмы, усеченного конуса и тора. Цилиндр занимает горизонтально проецирующее положение, призма – профильно проецирующее положение. Следовательно, линия пересечения будет строится из условия, что одна из пересекающихся поверхностей занимает проецирующее положение.

2. Строим линию пересечения горизонтально проецирующего цилиндра и усеченного конуса. Согласно условию, в цилиндр и конус можно вписать сферу, диаметр которой равен диаметру цилиндра. Применяем теорему Монжа, согласно которой, если две поверхности второго порядка описаны около третьей поверхности второго порядка или вписаны в нее, то линия их пересечения распадается на две кривые второго порядка, плоскости которых проходят через прямую, соединяющую точки пересечения линий касания. Поэтому на фронтальной проекции плоскости линии пересечения будут фронтально проецирующими. Все точки линии пересечения отображаются в виде прямых линий. Профильная проекция линии пересечения находится из принадлежности точек усеченному конусу.

3. Строим линию пересечения профильно проецирующей призмы с конусом и тором. Начинаем построение с горизонтальной проекции. Две боковые грани призмы являются фронтальными плоскостями уровня. На горизонтальной проекции они отображаются в виде прямых. Линия пересечения этих плоскостей с поверхностью конуса и тора совпадает с этими прямыми. Отмечаем на этих плоскостях точки. Фронтальную проекцию линии пересечения находим, привязывая точки к поверхности конуса и тора окружностями. Еще две боковые грани призмы являются горизонтальными плоскостями уровня. Нижняя грань призмы разрезает тор по окружности, верхняя разрезает цилиндр по окружности. Профильная проекция построенных линий пересечения совпадает с очерком призмы

4. Развертку призмы строим методом нормального сечения. Так как призма занимает профильно проецирующее положение, то боковые ребра призмы на фронтальной и горизонтальной проекции отображаются в натуральную величину. Поэтому линия пересечения переносится на развертку без дополнительных построений, так как на фронтальной проекции она отображена без искажения.

Эпюр №2А.

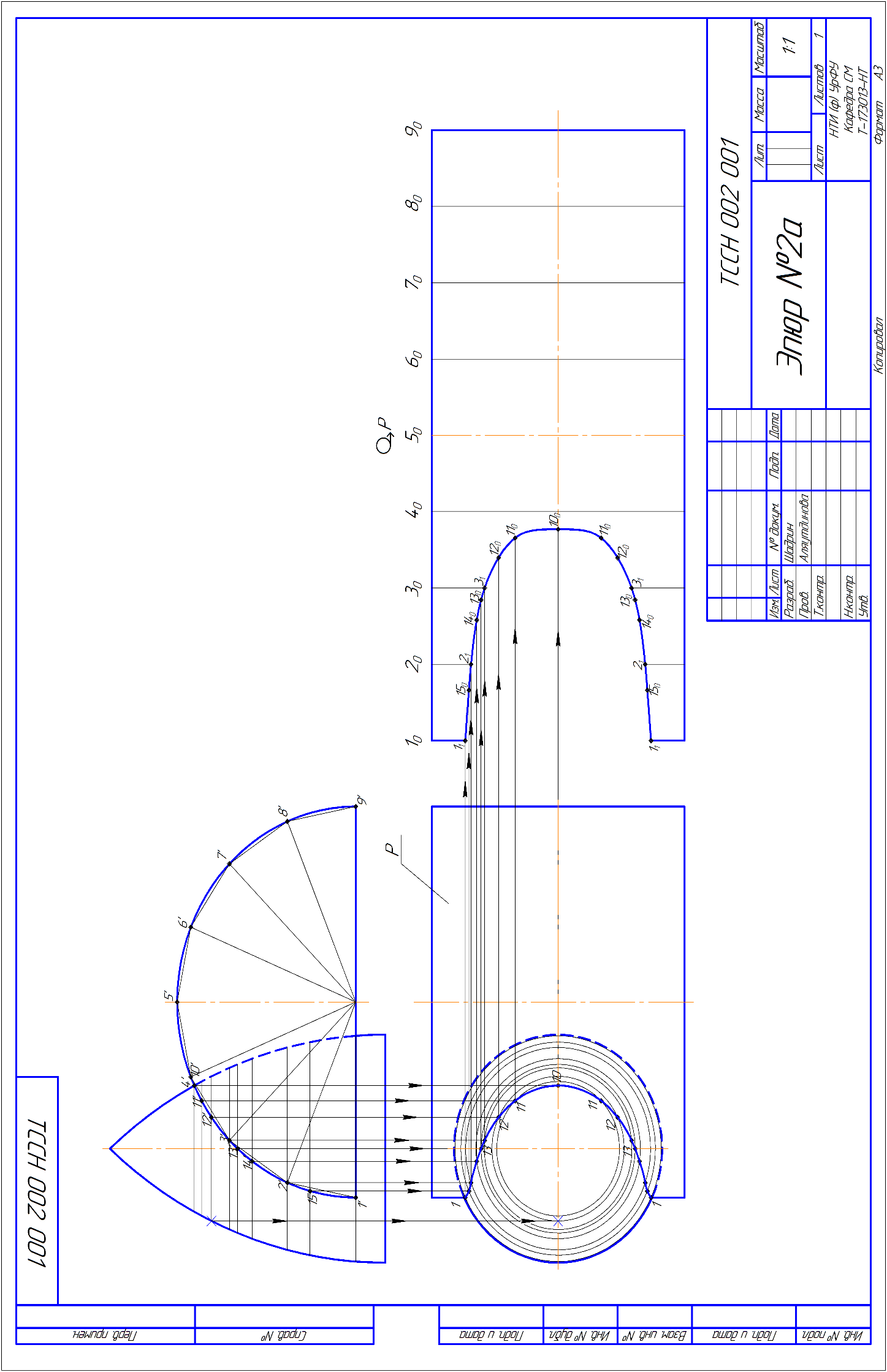
Ход решения:

1. Анализируем графическое условие эпюра:

Даны самопересекающийся тор и цилиндр. Ось вращения тора- горизонтально проецирующая прямая. Ось вращения цилиндра- фронтально проецирующая прямая. Следовательно, цилиндр – фронтально проецирующая поверхность. Линия пересечения заданных поверхностей будет строится из условия, что одна из пересекающихся поверхностей занимает проецирующее положение.

2.На фронтальной проекции линия пересечения совпадает с очерком цилиндра- окружностью.

3. Горизонтальную проекцию линии пересечения строим, привязывая точки к поверхности тора параллелями –окружностями

4. Строим пересечения тора с плоскостью, ограничивающий цилиндр на фронтальной проекции. Плоскость занимает положение горизонтальной плоскости уровня и разрезает тор по окружности.

5. На горизонтальной проекции эта окружность отображается без искажения.

6. Развертку цилиндрической поверхности строим методом аппроксимации – вписываем в цилиндр правильную призму. Число граней-16

7. Делим на фронтальной проекции полуокружность цилиндра на 8 равных частей.

8. Все точки линии пересечения переносим на развертку с горизонтальной проекции, так как образующие цилиндра отображаются на ней без искажения

ПРИЛОЖЕНИЕ 3

Варианты заданий к эпюру 1