
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Расчетно-пояснительная записка к курсовому проекту по ТММСтр 1 из 6Следующая ⇒
Расчетно-пояснительная записка к курсовому проекту по ТММ
на тему Проектирование и исследование механизмов колесного трактора
Выполнил: Абрамейцев А.А.
Проверил: Сёмов И.Н.
Пенза 2011 Содержание I. Структурный анализ и кинематическое исследование рычажного механизма………………………………………………………………………… 1.1 Структурный анализ механизма…………………………………………….. 1.2 Синтез механизма……………………………………………………………. 1.3 Построение схемы и исследование движения звеньев механизма……….. 1.4 Построение планов скоростей………………………………………..……… 1.5 Построение планов ускорений………………………………………………. 1.6 Построение кинематических диаграмм…………………………………… II. Силовой расчет механизма……………………………………………….. 2.1 Определение нагрузок на звенья механизма……………………………... 2.2 Определение реакций в кинематических парах механизма……………... 2.2.1 Силовой расчет группы звеньев 4 – 5……………………………….. 2.2.2 Силовой расчет группы звеньев 2 – 3………………………………… 2.2.3 Силовой расчет ведущего звена…………………………………...….. 2.3 Определение Ру методом жесткого рычага Н.Е. Жуковского…….……… III. Проектирование кулачкового механизма с плоским толкателем ….. 3.1 Задание и данные для расчетов………………………………………..…… 3.2 Построение диаграмм движения толкателя…………………………..…… 3.3 Определение минимального радиуса профиля кулачка………………….. 3.4 Построение профиля кулачка……………………………………………… IV. Проектирование кинематической схемы планетарного редуктора и построение картины эвольвентного зацепления зубчатых колёс…...….. 4.1 Описание схемы зубчатого механизма………………………………….… 4.2 Подбор чисел зубьев планетарного редуктора………………………….… 4.3 Построение схемы редуктора………………………………………….….... 4.4 Построение картины скоростей и плана угловых скоростей редуктора.... 4.5 Построение картины эвольвентного зацепления…………………...…….. 4.6 Определение коэффициента перекрытия…………………………….…… ЛИТЕРАТУРА………………………………………………………………….. Лист №1
I. Структурный анализ и кинематическое исследование рычажного механизма.
Исходные данные: α =90°; ОА=0, 08м; АВ = АС=0, 155м; AS2=AS4=AB/3; m2=m4=3, 0 кг; m3=m5=2, 8 кг; JS2= JS4=0, 02 кг ∙ м P макс = 5, 6 МПа; D =0, 14 мм;
Синтез механизма На рисунке 1 показана схема рычажного V-образного четырехтактного механизма двигателя внутреннего сгорания. Кривошип ОА (звено 1) вращается вокруг оси т.О со средней угловой скоростью ω 1.В то время, как т.А кривошипа перемещается из положения А0 в положение А'0, тогда т.В ползун-3 перейдет из положения В0 (нижняя мертвая точка) в положение В'0 (верхняя мертвая точка), т.е. пройдет путь равный S. S=2·LOA; S=2·0, 08=0, 16 м. Определим расстояние до центров тяжести шатунов: Из условия известно, AS2=AS4=AB/3 LAS2=LAS4=LAB/3; LAS2=LAS4=0, 31/3=0, 103м.
Построение схемы и исследование движения Звеньев механизма Выбираем масштабный коэффициент кинематической схемы
Определим масштабные длины звеньев механизма: шатуны
положение центров тяжести шатунов
ход ползуна
В принятом масштабе длин μ L по заданным размерам звеньев вычерчиваем кинематическую схему механизма. На чертеже помечаем положение т.О – центра вращения кривошипа, и положение неподвижных направляющих ОВ и ОС. Проводим траекторию т.А. Это окружность радиуса ОА. Делим траекторию т.А на 12 равных положений, получим т.А1, …, А12. Номеруем точки А в направление ω 1. Определим методом засечек положение точек В и С на их траекториях. Из каждой точки т.А откладываем отрезки, равным АВ=АС=160 мм. делаем засечку на направляющих ОВ и ОВ', получим т.В1, …, В12 и С1, …, С12. 1.4 Построение планов скоростей
Определение линейных скоростей точек механизма начинаем с входного звена 1(ОА). Так, модуль скорости точки А кривошипа, совершающего вращательное движение, определим из выражения: υ А= ω 1·LОА=199·0, 08=16 м/с
Направлен вектор скорости Далее определяем скорости точек структурной группы. Для этого составляем систему векторных уравнений, связывающих искомую скорость точки с известными скоростями точек.
Из уравнения (1) известно, что вектор скорости Из уравнения (2) известно, что вектор скорости В уравнениях четыре неизвестных параметра, которые могут быть определены в результате графического решения векторных уравнений, т.е. путем построения планов скоростей. Изображая скорость точки А отрезком Ра=41 мм, определим значение масштабного коэффициента:
Последовательность графоаналитического способа решения задачи рассмотрим на примере построения плана скоростей для седьмого положения механизма. На чертеже выбираем т. Р – полюс плана скоростей, проводим вектор Ра7 перпендикулярно кривошипу ОА7 в сторону его вращения. Конец вектора обозначим а7. Согласно уравнению (1) через точку а7 проводим линию действия Согласно уравнению (2) через точку а7 проводим линию действия Для определения скалярной величины любого из полученных векторов достаточно умножить соответствующий отрезок в мм на масштабный коэффициент плана скоростей:
Для нахождения скоростей точек S2 и S4 – центров тяжести звеньев 2 и 4 воспользуемся теоремой подобия:
Фигуры на плане скоростей должны быть пропорциональны фигурам на плане положений механизма. Скорости всех звеньев механизма и их отрезки в миллиметрах представлены в таблице 2. Планы скоростей для остальных положений механизма строим аналогично. Угловые скорости звеньев определяются с помощью построенных планов скоростей. Угловая скорость первого звена задана в исходных данных и равняется ω 1=199 рад/с; Модуль угловой скорости второго звена для второго положения механизма можно найти по формуле:
Модуль угловой скорости второго звена для седьмого положения механизма можно найти по формуле:
Таблица 2 Абсолютные и относительные скорости точек звеньев механизма и их отрезки в миллиметрах
Положение механизма | |||||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | ||||
| Pa, мм | 41 | 41 | 41 | 41 | 41 | 41 | 41 | 41 | 41 | 41 | 41 | 41 | |||
| υ А, м/с | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | |||
| Pb, мм | 0 | 25 | 54 | 80 | 77 | 50 | 0 | 49 | 74 | 80 | 60 | 31 | |||
| υ b, м/с | 0 | 5 | 11 | 16 | 15 | 10 | 0 | 8, 6 | 15 | 16 | 12 | 6 | |||
| PvC, мм | 80 | 76 | 48 | 0 | 52 | 79 | 80 | 61 | 31 | 0 | 34 | 62 | |||
| υ c, м/с | 16 | 15 | 9, 6 | 0 | 10, 4 | 16 | 16 | 12 | 6, 2 | 0 | 6, 8 | 12, 4 | |||
| ab, мм | 80 | 71 | 48 | 0 | 43 | 69 | 80 | 71 | 45 | 0 | 41 | 71 | |||
| υ ab, м/с | 16 | 14, 2 | 9, 6 | 0 | 8, 6 | 13, 8 | 16 | 14, 2 | 9 | 0 | 8, 2 | 14, 2 | |||
| са, мм | 0 | 38 | 68 | 80 | 68 | 41 | 0 | 36 | 67 | 80 | 69 | 40 | |||
| υ са, м/с | 0 | 7, 6 | 13, 6 | 16 | 13, 6 | 8, 2 | 0 | 7, 2 | 13, 4 | 16 | 13, 8 | 8 | |||
Значение угловых скоростей звеньев 2 и 4 представлены в таблице 3.
Таблица 3. Значение угловых скоростей шатуна АВ и АС в с-1
| Обозна -чение |
Положение механизма | |||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| ω 2 | 51 | 45 | 31 | 0 | 27 | 44 | 51 | 45 | 29 | 0 | 26 | 45 |
| ω 4 | 0 | 24 | 43 | 51 | 43 | 26 | 0 | 23 | 43 | 51 | 44 | 25 |
Направление угловой скорости звена АВ определяется следующим образом. Переносим мысленно вектор  с плана скоростей в точку В шатуна 2 и наблюдаем направление поворота этого звена вокруг точки А.
с плана скоростей в точку В шатуна 2 и наблюдаем направление поворота этого звена вокруг точки А.
1.5 Построение планов ускорений
Построение планов ускорений рассмотрим для второго положения механизма. Так как кривошип ОА вращается с постоянной угловой скоростью, то точка А будет иметь только нормальное ускорение, величина которого равна:

а направленно оно параллельно звену ОА от точки А к точке О.
Определяем масштабный коэффициент плана ускорений:

Последовательность построения плана ускорений рассмотрим для седьмого положения механизма.
Из произвольной точки π – полюса плана ускорений откладываем вектор  параллельно звену ОА от точки А к точке О.
параллельно звену ОА от точки А к точке О.
Для построения точки В и В' составим и решим графические уравнения:

Ускорение  направлено параллельно ОВ проведенное через полюс
направлено параллельно ОВ проведенное через полюс  .
.
Ускорение 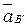 направлено параллельно ОВ' проведенное через полюс
направлено параллельно ОВ' проведенное через полюс  .
.
Определим модули нормальных ускорений:

Нормальное ускорение  направлено параллельно звену АВ от точки В к точке А (центру вращения).
направлено параллельно звену АВ от точки В к точке А (центру вращения).
Нормальное ускорение 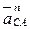 направлено параллельно звену АС от точки С к точке А.
направлено параллельно звену АС от точки С к точке А.
Для 1 положения 
Для 6 положения 
Для 8 положения 
Тангенциальные составляющие ускорений  и
и  по абсолютной величине неизвестны, но известны по направлению. Они направлены перпендикулярно соответствующим звеньям механизма АВ и АС или перпендикулярно нормальным составляющим.
по абсолютной величине неизвестны, но известны по направлению. Они направлены перпендикулярно соответствующим звеньям механизма АВ и АС или перпендикулярно нормальным составляющим.
Согласно первому векторному уравнению через точку а плана ускорений проводим прямую, направленную вдоль звена АВ в направлении от точки В к точке А и на ней откладываем отрезок a  =8 мм, величина которого в масштабе соответствует величине вектора нормальной составляющей ускорения
=8 мм, величина которого в масштабе соответствует величине вектора нормальной составляющей ускорения 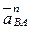 .
.
Через точку  перпендикулярно звену АВ (или тоже самое, что перпендикулярно
перпендикулярно звену АВ (или тоже самое, что перпендикулярно  ) проводим направление вектора тангенциального ускорения
) проводим направление вектора тангенциального ускорения  , до пересечения с линей действия вектора
, до пересечения с линей действия вектора  (параллельно к ОВ, проведенный через полюс
(параллельно к ОВ, проведенный через полюс  ). Получим точку В.
). Получим точку В.
Согласно второму векторному уравнению через точку а плана ускорений проводим прямую, направленную вдоль звена АC в направлении от точки C к точке А и на ней откладываем отрезок  =3 мм. величина которого в масштабе соответствует величине вектора нормальной составляющей ускорения
=3 мм. величина которого в масштабе соответствует величине вектора нормальной составляющей ускорения  .
.
Через точку  перпендикулярно звену АC проводим направление вектора тангенциального ускорения
перпендикулярно звену АC проводим направление вектора тангенциального ускорения  , до пересечения с линей действия вектора
, до пересечения с линей действия вектора 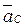 (параллельно к ОC, проведенный через полюс
(параллельно к ОC, проведенный через полюс  ). Получим точку C.
). Получим точку C.
Для определения ускорений точек S2 и S4 – центров тяжести звена 2 и звена 4 воспользуемся теоремой подобия.


Определяем действительное значение ускорений:

План ускорений для положений механизма 1 и 6 строим аналогично. Ускорение всех точек звеньев механизма и их отрезки сводим в таблицу 4.
Таблицу 4. Абсолютные и относительные ускорение точек
звеньев механизма и их отрезки в миллиметрах
| Обозначение | Единица | Положение механизма | ||||
| 1 | 6 | 8 | ||||
|
| мм | 48 | 48 | 48 | ||
| аА | м/с2 | 3168 | 3168 | 3168 | ||
|
| мм | 41 | 78 | 29 | ||
| аB | м/с2 | 2050 | 3900 | 1450 | ||

| мм | 62 | 15 | 47 | ||
| АC | м/с2 | 3100 | 750 | 2350 | ||
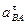
| мм | 2700 | 0 | 2600 | ||

| м/с2 | 54 | 0 | 52 | ||

| мм | 31 | 62 | 32 | ||

| м/с2 | 1550 | 3100 | 1600 | ||
Угловые ускорения звеньев определяются на основе построенных планов ускорений.
Входное звено 1 вращается равномерно с постоянной угловой скоростью. Следовательно, его угловое ускорение равно нулю:
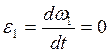
Модули угловых ускорений второго и четвертого звеньев для второго положения механизма можно найти по формулам:

Таблица 5. Значение угловых ускорений шатуна АВ и АВ' в с-2
| Обозначение | Единица | Положение механизма | ||
| 1 | 6 | 8 | ||
| ε 2 | с-2 | 8709 | 0 | 8387 |
| ε 4 | с-2 | 5000 | 10000 | 5161 |
Определим направления угловых ускорений звеньев 2 и 4. Чтобы определить направление углового ускорения ε 2 необходимо вектор относительного тангенциального ускорения  с плана ускорений перенести в точку В механизма, а точку А условно закрепить.
с плана ускорений перенести в точку В механизма, а точку А условно закрепить.
1.6 Построение диаграммы перемещения S ( t ), скорости υ ( t ) и ускорения a ( t ) точки В ползуна 3
По оси t откладываем отрезок L=240 мм. Данный отрезок соответствует времени оборота кривошипа.

Делим отрезок L на 12 равных частей и получаем точки 0, 1, …, 11, 12. Для построения диаграммы S(t) нужно из точек 0, 1, …, 11, 12 отложить ординаты, соответствующие перемещению точки В. Полученные точки 1', …, 11' соединяем плавной кривой.
Для построения диаграммы υ (t) воспользуемся методом дифференцирования (метод хорд). Криволинейные участки графика S(t), соответствующие интервалам оси t, заменяем хордами. Выбираем произвольной длинны полюсное расстояние Н1=36 мм. Из полюса P1 проводим лучи параллельные соответствующий хордам участков заданной кривой до пересечения с осью ординат. Из середины интервалов проводим перпендикуляры к оси абсцисс до пересечения с соответствующими линиями. Полученные точки 1'', …, 11'' соединяем плавной кривой.
Масштаб оси υ равен:
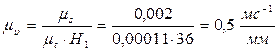
Диаграмму a(t) построим аналогичным способом (методом хорд) путем дифференцирования диаграммы υ (t). Выбираем произвольной длинны полюсное расстояние Н2=45 мм.
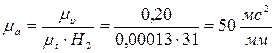
Лист №2
Группа звеньев 4 – 5
Изображаем группу звеньев 4 – 5 в масштабе μ L=0, 002 м/мм.
Рассмотрим силы, действующие на группу звеньев 4 – 5.
В центре тяжести звеньев S4 и S5 приложены силы веса G4, G5, направлены вертикально вниз.
Силу инерции  прикладываем в точке Т4 и направляем противоположно вектору ускорения центра тяжести звена 4. Точку Т4 находим, откладывая от направления линии действия силы инерции PИ4 приложенной в центре тяжести S4, плечо h4 таким образом, чтобы сила инерции
прикладываем в точке Т4 и направляем противоположно вектору ускорения центра тяжести звена 4. Точку Т4 находим, откладывая от направления линии действия силы инерции PИ4 приложенной в центре тяжести S4, плечо h4 таким образом, чтобы сила инерции  , приложенная в точке Т4, создавала момент относительно S4 того же направления, что и момент MИ4.
, приложенная в точке Т4, создавала момент относительно S4 того же направления, что и момент MИ4.
Силу инерции  прикладываем в точке С и направляем противоположно вектору ускорения центра тяжести звена 5.
прикладываем в точке С и направляем противоположно вектору ускорения центра тяжести звена 5.
Сила  (направлена противоположно скорости точки С)
(направлена противоположно скорости точки С)
Освобожденные связи заменяем реакциями.
В шарнире А со стороны звена 1 действуют реакции связи. Обозначим её R14. Она не известна ни по величине, ни по направлению. Для упрощения решения задачи разложим эту реакцию на две составляющие: нормальную  направленную вдоль линии AС звена 4, и касательную
направленную вдоль линии AС звена 4, и касательную  , направленную перпендикулярно линии AС звена 4.
, направленную перпендикулярно линии AС звена 4.
Под действием всех внешних сил, сил инерции и реакций связей структурная группа находится в равновесии. Исходя из условий равновесия, составим уравнение моментов всех сил, действующих на группу, относительно точки С (при этом  для звена 4) и определим касательную составляющую силы
для звена 4) и определим касательную составляющую силы  .
.
Будем считать моменты, действующие против часовой стрелки, положительными, а по часовой – отрицательными. Плечи сил определяются непосредственным замером на чертеже в миллиметрах и обозначаются буквой h с индексом соответствующей силы.
Исходя из условия равновесия звена 4 запишем:

Составим векторное уравнение равновесия сил, действующих на группу 4 – 5 (  ).
).

Полученное векторное уравнение имеет два неизвестных и может быть легко решено графическим методом, путем построения многоугольника сил. Равенство говорит о том, что этот многоугольник сил должен быть замкнутым.
Построение плана сил начинаем с линии действия реакции 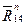 , затем откладываем из произвольной точки «1» на этой линии в масштабе μ Р, удобном для построения, все силы с учетом их направления.
, затем откладываем из произвольной точки «1» на этой линии в масштабе μ Р, удобном для построения, все силы с учетом их направления.
Принимаем масштабный коэффициент плана сил равным
μ Р=100 Н/мм.
Тогда масштабные (на чертеже) отрезки сил в миллиметрах определятся как частное от деления абсолютной величины силы на масштабный коэффициент, значения каждой силы в миллиметрах запишем в нижний строчке векторного уравнения (под значением силы в Ньютонах)
Затем строим по порядку силы, геометрически складывая их. Из конца последнего вектора  проводим линию действия реакции
проводим линию действия реакции  и соединяем линией действия реакции
и соединяем линией действия реакции  .
.
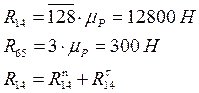
Определим реакцию в шарнире C– R54. Для этого рассмотрим условие равновесия пятого звена:
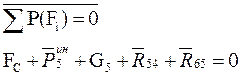
Воспользуемся планов сил для звена 5.


Группа звеньев 2 – 3
Изображаем группу звеньев 2 – 3 в масштабе μ L=0, 002 м/мм.
Рассмотрим силы, действующие на группу звеньев 2 – 3.
В центре тяжести звеньев S2 и S3 приложены силы веса G2, G3, направлены вертикально вниз.
Силу инерции  прикладываем в точке Т2 и направляем противоположно вектору ускорения центра тяжести звена 2. Точку Т2 находим, откладывая от направления линии действия силы инерции
прикладываем в точке Т2 и направляем противоположно вектору ускорения центра тяжести звена 2. Точку Т2 находим, откладывая от направления линии действия силы инерции  приложенной в центре тяжести S2, плечо h2 таким образом, чтобы сила инерции
приложенной в центре тяжести S2, плечо h2 таким образом, чтобы сила инерции  , приложенная в точке Т2, создавала момент относительно S2 того же направления, что и момент
, приложенная в точке Т2, создавала момент относительно S2 того же направления, что и момент  .
.
Силу инерции PИ3 прикладываем в точке В и направляем противоположно вектору ускорения центра тяжести звена 2.
Сила  направлена в сторону скорости точку В.
направлена в сторону скорости точку В.
Освобожденные связи заменяем реакциями.
В шарнире А со стороны звена 1 действуют реакции связи. Обозначим её R12. Она не известна ни по величине, ни по направлению. Для упрощения решения задачи разложим эту реакцию на две составляющие: нормальную 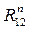 направленную вдоль линии AB звена 2, и касательную
направленную вдоль линии AB звена 2, и касательную  , направленную перпендикулярно линии AB звена 2.
, направленную перпендикулярно линии AB звена 2.
Под действием всех внешних сил, сил инерции и реакций связей структурная группа находится в равновесии. Исходя из условий равновесия, составим уравнение моментов всех сил, действующих на группу, относительно точки В (при этом  для звена 2) и определим касательную составляющую силы
для звена 2) и определим касательную составляющую силы  .
.
Будем считать моменты, действующие против часовой стрелки, положительными, а по часовой – отрицательными. Плечи сил определяются непосредственным замером на чертеже в миллиметрах и обозначаются буквой h с индексом соответствующей силы.
Исходя из условия равновесия звена 2 запишем:
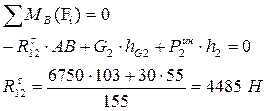
Составим векторное уравнение равновесия сил, действующих на группу 2 – 3 (  ).
).

Полученное векторное уравнение имеет два неизвестных и может быть легко решено графическим методом, путем построения многоугольника сил. Равенство говорит о том, что этот многоугольник сил должен быть замкнутым.
Построение плана сил начинаем с линии действия реакции  , на ней в произвольном месте намечаем точку, из которой последовательно одна за другой откладываем в масштабе все силы:
, на ней в произвольном месте намечаем точку, из которой последовательно одна за другой откладываем в масштабе все силы:
Принимаем масштабный коэффициент плана сил равным
μ Р=500 Н/мм.
Тогда масштабные (на чертеже) отрезки сил в миллиметрах определятся как частное от деления абсолютной величины силы на масштабный коэффициент, значения сил в миллиметрах пишем в уравнении под значениями в Ньютонах
Затем строим по порядку силы, геометрически складывая и действия реакции. Из конца построения  проводим линию действия реакции
проводим линию действия реакции  до пересечения с линией
до пересечения с линией 
. 
Определим реакцию в шарнире B – R23. Для этого рассмотрим условие равновесия третьего звена:

При помощи плана сил  =112мм,
=112мм,  =56000Н
=56000Н
Лист №3
С плоским толкателем
Содержание задания.
1. Построить в произвольном масштабе заданный закон изменения второй производной перемещения толкателя по углу поворота кулачка

2. Методом графического интегрирования построить графики

3. Графически исключив параметр φ из графиков

построить совмещенный график 
Определить минимальный радиус кулачка.
4. Методом обращения движения построить практический (он же рабочий) профиль кулачка.
Задание и данные для расчетов
Задание. Спроектировать кулачковый механизм с роликовым толкателем. Дано:
1. схема кулачкового механизма (рис. 3.1);
2. закон изменения аналога ускорения толкателя кулачкового механизма (рис. 3.1);
3. исходные данные в таблице 1.
Таблица 1
| Наименование параметра | Обозначение | Единицы | Числовое значение |
| Угол выстоя | φ вс | град | 40 |
| Ход толкателя в кулачковом механизме | H | мм | 57 |
| Угол удаления | φ у | град | 105 |
| Угол возвращения | φ в | град | 105 |
| Максимальный угол давления в кулачковом механизме | υ доп | град | 25 |

Рисунок 3.1 – Схема кулачкового механизма и закон аналога ускорений
Профиля кулачка
Для определения минимального радиуса кулачка Rmin строится дополнительная диаграмма 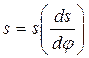 методом исключения угла φ
методом исключения угла φ
в масштабе  по данным таблицы 2.
по данным таблицы 2.
Для этого проводим взаимно перпендикулярные оси. Ось ординат обозначим через S, а ось абсцисс через S´ . По оси S производим разметку пути толкателя. В направлении, перпендикулярном движению толкателя откладываем для каждого положения величины S´ вправо при движении толкателя вверх. Построенные точки соединяем плавной кривой.
Строим вторую половину диаграммы, откладывая величины S´ влево при движении толкателя вниз.
По диаграмме  определяем допустимую область центров вращения кулачка. Для этого из концов отрезков максимальных значений S´ проводим лучи под углом υ доп=25° к направлению движения толкателя.
определяем допустимую область центров вращения кулачка. Для этого из концов отрезков максимальных значений S´ проводим лучи под углом υ доп=25° к направлению движения толкателя.
Эти лучи пересекаются в точке О1, которая определяет положение оси вращения кулачка при его минимальных размерах.
ОО1 представляет собой минимальный радиус профиля кулачка Rmin= ОО1= 22 мм. Этот размер берется прямо с чертежа, так как диаграмма  была построена в масштабе
была построена в масштабе 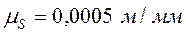
Построение профиля кулачка
Начинаем построение профиля кулачка (без ролика).
В произвольной точки О (ось вращения кулачка) проводим окружность радиусом Rmin= 22 мм., то есть построение производим в масштабе  . Через ось О проводим линию 0 – 0 движение толкателя.
. Через ось О проводим линию 0 – 0 движение толкателя.
В соответствии с разметкой фазовых углов на графике S" откладываем, начиная от действительной линии движения толкателя, в направлении противоположном вращению кулачка, фазовые углы φ у=105° и φ в=105°.
Отмечаем на окружности Rmin точки 6, 12.
Делим фазовые углы на шесть равных частей (каждая часть равна 17.5°). Точки деления на окружности Rmin соединяем радиусами (лучами) с центром вращения кулачка – точкой О.
От окружности радиуса Rmin вдоль этих радиусов от соответствующей точки откладываем перемещения толкателя из таблицы 2 для  .
.
Эти перемещения показаны толстыми линиями.
Соединяем полученные точки плавной кривой, получаем центровой (теоретический) профиль кулачка. Этот профиль является рабочим профилем кулачка с толкателем без ролика.
Определяем минимальный радиус кривизны центрового профиля кулачка ρ min как радиус вписанной окружности выпуклого участка профиля кулачка, где кривизны окажется наибольшей. На этом участке произвольно выбираем три точки 3, 4, 5 и соединяем их двумя хордами. В середине хорд восстанавливаем к ним перпендикуляры, точку пересечения которых М принимаем за центр вписанной окружности. Получаем ρ min=40 мм.
Действительный профиль кулачка найдем как эквидистантную кривую, отстоящую от центрального профиля на расстоянии, равном радиусу ролика.
Радиус ролика выбирается наименьшим из условий:

Принимаем rp=18 мм.
Для получения действительного (рабочего) профиля кулачка на его центровом профиле выбираем ряд точек, из которых проводим окружности радиусом, равным радиусу ролика rp.
Огибающая этих окружностей (внутренняя) и является действительным (рабочем) профилем кулачка.
Заключение
Одной из ведущих отраслей современной техники является машиностроение. По уровню развития машиностроения судят о развитии производительных сил в целом. Прогресс машиностроения в свою очередь определяется созданием новых высокопроизводительных и надёжных машин. Решение этой важнейшей проблемы основывается на комплексном использовании результатов многих дисциплин и, в первую очередь, теории механизмов и машин.
В первом разделе провел структурное и кинематическое исследование механизма двигателя внутреннего сгорания. Также провел структурное исследование механизма, кинематическое исследование механизма. Построил план механизма, план скоростей, угловые ускорения звеньев, кинематические диаграммы, диаграммы перемещения поршня, диаграмма скоростей поршня, ускорение поршня.
Во втором разделе произвел силовой (кинетостатический ) расчет механизма двигателя внутреннего сгорания. Определил силы, действующие на механизм: силы движущейся силы инерции звеньев. Определил реакцию в кинематических прах механизма (расчет группы звеньев 2 -3, расчет группы звеньев 4-5).Провел силовой расчет входного звена механизма. После этого определил уравновешиваюшие силы методом жесткого рычага Н.Е.Жуковского. Проверил кинетостатическое исследование механизма.
СПИСОК ЛИТЕРАТУРЫ
1. Артоболевский И. И. Теория механизмов и машин: Учеб. для втузов. – 4-е изд., перераб. и доп. – М.: Наука, 1975. – 640 с.
2. Артоболевский И. И. и Эндельштейн Б. В. Сборник задач по теории механизмов и машин. Главная редакция физико-математической литературы издательства «Наука», 1975. – 256 с.
3. Анисимов В.П. Теория механизмов и машин: учебное пособие к курсовому проектированию. – Пенза: ПГАСА, 2003. – 87 с.
5. Пономарёв В. А. Теория механизмов и машин. Задания для курсового проекта. – М.: 1989. – 55 с.
6. Пономарёв. В. А. Теория механизмов и машин. Методические указания по изучению дисциплины и выполнению курсового проекта. – М.: 1989. – 84 с.
7. Попов С. А. Курсовое проектирование по теории механизмов и машин. – М.: Высшая школа, 1986 – 225 с.
Расчетно-пояснительная записка к курсовому проекту по ТММ
на тему
Проектирование и исследование механизмов колесного трактора
Выполнил: Абрамейцев А.А.
Проверил: Сёмов И.Н.
Пенза 2011
Содержание
I. Структурный анализ и кинематическое исследование рычажного механизма…………………………………………………………………………
1.1 Структурный анализ механизма……………………………………………..
1.2 Синтез механизма…………………………………………………………….
1.3 Построение схемы и исследование движения звеньев механизма………..
1.4 Построение планов скоростей………………………………………..………
1.5 Построение планов ускорений……………………………………………….
1.6 Построение кинематических диаграмм……………………………………
II. Силовой расчет механизма………………………………………………..
2.1 Определение нагрузок на звенья механизма……………………………...
2.2 Определение реакций в кинематических парах механизма……………...
2.2.1 Силовой расчет группы звеньев 4 – 5………………………………..
2.2.2 Силовой расчет группы звеньев 2 – 3…………………………………
2.2.3 Силовой расчет ведущего звена…………………………………...…..
2.3 Определение Ру методом жесткого рычага Н.Е. Жуковского…….………
III. Проектирование кулачкового механизма с плоским толкателем …..
3.1 Задание и данные для расчетов………………………………………..……
3.2 Построение диаграмм движения толкателя…………………………..……
3.3 Определение минимального радиуса профиля кулачка…………………..
3.4 Построение профиля кулачка………………………………………………
IV. Проектирование кинематической схемы планетарного редуктора и построение картины эвольвентного зацепления зубчатых колёс…...…..
4.1 Описание схемы зубчатого механизма………………………………….…
4.2 Подбор чисел зубьев планетарного редуктора………………………….…
4.3 Построение схемы редуктора………………………………………….…....
4.4 Построение картины скоростей и плана угловых скоростей редуктора....
4.5 Построение картины эвольвентного зацепления…………………...……..
4.6 Определение коэффициента перекрытия…………………………….……
ЛИТЕРАТУРА…………………………………………………………………..
Лист №1
Последнее изменение этой страницы: 2019-04-09; Просмотров: 400; Нарушение авторского права страницы