
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
I . Структурный анализ и кинематическое исследование рычажного механизма.
Исходные данные: α =90°; ОА=0, 08м; АВ = АС=0, 155м; AS2=AS4=AB/3; m2=m4=3, 0 кг; m3=m5=2, 8 кг; JS2= JS4=0, 02 кг ∙ м P макс = 5, 6 МПа; D =0, 14 мм;
Структурный анализ механизма
Механизм включает в себя 5 звеньев: 1 – кривошип, 2, 4 – шатун, 3, 5 – ползун, 6 – стойка. Всего 5 подвижных звеньев в данном механизме.
Соприкосновение звеньев и их относительное движение образуют кинематическую пару (КП). 6, 1 (стойка – кривошип) это вращательная КП, низшая, 5 класс. 1, 2 (кривошип шатун) это вращательная КП, низшая, 5 класс. 1, 4 (кривошип – шатун) это вращательная КП, низшая, 5 класс. 2, 3 (шатун – ползун) это вращательная КП, низшая, 5 класс. 4, 5 (шатун – ползун) это вращательная КП, низшая, 5 класс. 3, 6 (ползун – стойка) это вращательная КП, низшая, 5 класс. 5, 6 (ползун – стойка) это вращательная КП, низшая, 5 класс. Всего 7 кинематических пар в данном механизме.
Определяем степень подвижности механизма по формуле П.Л. Чебышева: W =3 n -2 p 5 - p 4, где n=5 – число подвижных звеньев; p5=7 – число кинематических пар пятого класса; p4=0 – число кинематических пар четвертого класса. Определяем класс механизма. Для этого разложим механизм на группы Ассура, на начальный механизм (W=1) состоящие из 1-го входного звена и 1-й кинематической пары. И простейшие структурные группы (W=0) состоящие из 2-х звеньев и 3-х кинематических пар. Разложение механизма на группы Ассура и определение класса механизма выполнено согласно классификации Ассура – Артоболевского. В таблице 1 приведен рычажный механизм V-образного двигателя внутреннего сгорания, разложенный на группы Аcсура (при разложении на группы Ассура следует обязательно соблюдать взаимное расположение звеньев).
Таблица 1 Структурное исследование механизма
Класс механизма определяется наивысшим классом группы Ассура которая входит в состав механизма. Рассматриваемый механизм 2-го класса.
Формула строения механизма запишется в следующем виде:
I(6, 1) II(4, 5)
Синтез механизма На рисунке 1 показана схема рычажного V-образного четырехтактного механизма двигателя внутреннего сгорания. Кривошип ОА (звено 1) вращается вокруг оси т.О со средней угловой скоростью ω 1.В то время, как т.А кривошипа перемещается из положения А0 в положение А'0, тогда т.В ползун-3 перейдет из положения В0 (нижняя мертвая точка) в положение В'0 (верхняя мертвая точка), т.е. пройдет путь равный S. S=2·LOA; S=2·0, 08=0, 16 м. Определим расстояние до центров тяжести шатунов: Из условия известно, AS2=AS4=AB/3 LAS2=LAS4=LAB/3; LAS2=LAS4=0, 31/3=0, 103м.
Построение схемы и исследование движения Звеньев механизма Выбираем масштабный коэффициент кинематической схемы
Определим масштабные длины звеньев механизма: шатуны
положение центров тяжести шатунов
ход ползуна
В принятом масштабе длин μ L по заданным размерам звеньев вычерчиваем кинематическую схему механизма. На чертеже помечаем положение т.О – центра вращения кривошипа, и положение неподвижных направляющих ОВ и ОС. Проводим траекторию т.А. Это окружность радиуса ОА. Делим траекторию т.А на 12 равных положений, получим т.А1, …, А12. Номеруем точки А в направление ω 1. Определим методом засечек положение точек В и С на их траекториях. Из каждой точки т.А откладываем отрезки, равным АВ=АС=160 мм. делаем засечку на направляющих ОВ и ОВ', получим т.В1, …, В12 и С1, …, С12. 1.4 Построение планов скоростей
Определение линейных скоростей точек механизма начинаем с входного звена 1(ОА). Так, модуль скорости точки А кривошипа, совершающего вращательное движение, определим из выражения: υ А= ω 1·LОА=199·0, 08=16 м/с
Направлен вектор скорости Далее определяем скорости точек структурной группы. Для этого составляем систему векторных уравнений, связывающих искомую скорость точки с известными скоростями точек.
Из уравнения (1) известно, что вектор скорости Из уравнения (2) известно, что вектор скорости В уравнениях четыре неизвестных параметра, которые могут быть определены в результате графического решения векторных уравнений, т.е. путем построения планов скоростей. Изображая скорость точки А отрезком Ра=41 мм, определим значение масштабного коэффициента:
Последовательность графоаналитического способа решения задачи рассмотрим на примере построения плана скоростей для седьмого положения механизма. На чертеже выбираем т. Р – полюс плана скоростей, проводим вектор Ра7 перпендикулярно кривошипу ОА7 в сторону его вращения. Конец вектора обозначим а7. Согласно уравнению (1) через точку а7 проводим линию действия Согласно уравнению (2) через точку а7 проводим линию действия Для определения скалярной величины любого из полученных векторов достаточно умножить соответствующий отрезок в мм на масштабный коэффициент плана скоростей:
Для нахождения скоростей точек S2 и S4 – центров тяжести звеньев 2 и 4 воспользуемся теоремой подобия:
Фигуры на плане скоростей должны быть пропорциональны фигурам на плане положений механизма. Скорости всех звеньев механизма и их отрезки в миллиметрах представлены в таблице 2. Планы скоростей для остальных положений механизма строим аналогично. Угловые скорости звеньев определяются с помощью построенных планов скоростей. Угловая скорость первого звена задана в исходных данных и равняется ω 1=199 рад/с; Модуль угловой скорости второго звена для второго положения механизма можно найти по формуле:
Модуль угловой скорости второго звена для седьмого положения механизма можно найти по формуле:
Таблица 2 Абсолютные и относительные скорости точек звеньев механизма и их отрезки в миллиметрах
Положение механизма | |||||||||||||||||||||||||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | ||||||||||||||||||||||||
| Pa, мм | 41 | 41 | 41 | 41 | 41 | 41 | 41 | 41 | 41 | 41 | 41 | 41 | |||||||||||||||||||||||
| υ А, м/с | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | |||||||||||||||||||||||
| Pb, мм | 0 | 25 | 54 | 80 | 77 | 50 | 0 | 49 | 74 | 80 | 60 | 31 | |||||||||||||||||||||||
| υ b, м/с | 0 | 5 | 11 | 16 | 15 | 10 | 0 | 8, 6 | 15 | 16 | 12 | 6 | |||||||||||||||||||||||
| PvC, мм | 80 | 76 | 48 | 0 | 52 | 79 | 80 | 61 | 31 | 0 | 34 | 62 | |||||||||||||||||||||||
| υ c, м/с | 16 | 15 | 9, 6 | 0 | 10, 4 | 16 | 16 | 12 | 6, 2 | 0 | 6, 8 | 12, 4 | |||||||||||||||||||||||
| ab, мм | 80 | 71 | 48 | 0 | 43 | 69 | 80 | 71 | 45 | 0 | 41 | 71 | |||||||||||||||||||||||
| υ ab, м/с | 16 | 14, 2 | 9, 6 | 0 | 8, 6 | 13, 8 | 16 | 14, 2 | 9 | 0 | 8, 2 | 14, 2 | |||||||||||||||||||||||
| са, мм | 0 | 38 | 68 | 80 | 68 | 41 | 0 | 36 | 67 | 80 | 69 | 40 | |||||||||||||||||||||||
| υ са, м/с | 0 | 7, 6 | 13, 6 | 16 | 13, 6 | 8, 2 | 0 | 7, 2 | 13, 4 | 16 | 13, 8 | 8 | |||||||||||||||||||||||
Значение угловых скоростей звеньев 2 и 4 представлены в таблице 3.
Таблица 3. Значение угловых скоростей шатуна АВ и АС в с-1
| Обозна -чение |
Положение механизма | |||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| ω 2 | 51 | 45 | 31 | 0 | 27 | 44 | 51 | 45 | 29 | 0 | 26 | 45 |
| ω 4 | 0 | 24 | 43 | 51 | 43 | 26 | 0 | 23 | 43 | 51 | 44 | 25 |
Направление угловой скорости звена АВ определяется следующим образом. Переносим мысленно вектор  с плана скоростей в точку В шатуна 2 и наблюдаем направление поворота этого звена вокруг точки А.
с плана скоростей в точку В шатуна 2 и наблюдаем направление поворота этого звена вокруг точки А.
1.5 Построение планов ускорений
Построение планов ускорений рассмотрим для второго положения механизма. Так как кривошип ОА вращается с постоянной угловой скоростью, то точка А будет иметь только нормальное ускорение, величина которого равна:

а направленно оно параллельно звену ОА от точки А к точке О.
Определяем масштабный коэффициент плана ускорений:

Последовательность построения плана ускорений рассмотрим для седьмого положения механизма.
Из произвольной точки π – полюса плана ускорений откладываем вектор  параллельно звену ОА от точки А к точке О.
параллельно звену ОА от точки А к точке О.
Для построения точки В и В' составим и решим графические уравнения:

Ускорение  направлено параллельно ОВ проведенное через полюс
направлено параллельно ОВ проведенное через полюс  .
.
Ускорение 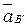 направлено параллельно ОВ' проведенное через полюс
направлено параллельно ОВ' проведенное через полюс  .
.
Определим модули нормальных ускорений:

Нормальное ускорение  направлено параллельно звену АВ от точки В к точке А (центру вращения).
направлено параллельно звену АВ от точки В к точке А (центру вращения).
Нормальное ускорение 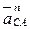 направлено параллельно звену АС от точки С к точке А.
направлено параллельно звену АС от точки С к точке А.
Для 1 положения 
Для 6 положения 
Для 8 положения 
Тангенциальные составляющие ускорений  и
и  по абсолютной величине неизвестны, но известны по направлению. Они направлены перпендикулярно соответствующим звеньям механизма АВ и АС или перпендикулярно нормальным составляющим.
по абсолютной величине неизвестны, но известны по направлению. Они направлены перпендикулярно соответствующим звеньям механизма АВ и АС или перпендикулярно нормальным составляющим.
Согласно первому векторному уравнению через точку а плана ускорений проводим прямую, направленную вдоль звена АВ в направлении от точки В к точке А и на ней откладываем отрезок a  =8 мм, величина которого в масштабе соответствует величине вектора нормальной составляющей ускорения
=8 мм, величина которого в масштабе соответствует величине вектора нормальной составляющей ускорения 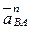 .
.
Через точку  перпендикулярно звену АВ (или тоже самое, что перпендикулярно
перпендикулярно звену АВ (или тоже самое, что перпендикулярно  ) проводим направление вектора тангенциального ускорения
) проводим направление вектора тангенциального ускорения  , до пересечения с линей действия вектора
, до пересечения с линей действия вектора  (параллельно к ОВ, проведенный через полюс
(параллельно к ОВ, проведенный через полюс  ). Получим точку В.
). Получим точку В.
Согласно второму векторному уравнению через точку а плана ускорений проводим прямую, направленную вдоль звена АC в направлении от точки C к точке А и на ней откладываем отрезок  =3 мм. величина которого в масштабе соответствует величине вектора нормальной составляющей ускорения
=3 мм. величина которого в масштабе соответствует величине вектора нормальной составляющей ускорения  .
.
Через точку  перпендикулярно звену АC проводим направление вектора тангенциального ускорения
перпендикулярно звену АC проводим направление вектора тангенциального ускорения  , до пересечения с линей действия вектора
, до пересечения с линей действия вектора 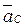 (параллельно к ОC, проведенный через полюс
(параллельно к ОC, проведенный через полюс  ). Получим точку C.
). Получим точку C.
Для определения ускорений точек S2 и S4 – центров тяжести звена 2 и звена 4 воспользуемся теоремой подобия.


Определяем действительное значение ускорений:

План ускорений для положений механизма 1 и 6 строим аналогично. Ускорение всех точек звеньев механизма и их отрезки сводим в таблицу 4.
Таблицу 4. Абсолютные и относительные ускорение точек
звеньев механизма и их отрезки в миллиметрах
| Обозначение | Единица | Положение механизма | ||||
| 1 | 6 | 8 | ||||
|
| мм | 48 | 48 | 48 | ||
| аА | м/с2 | 3168 | 3168 | 3168 | ||
|
| мм | 41 | 78 | 29 | ||
| аB | м/с2 | 2050 | 3900 | 1450 | ||

| мм | 62 | 15 | 47 | ||
| АC | м/с2 | 3100 | 750 | 2350 | ||
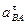
| мм | 2700 | 0 | 2600 | ||

| м/с2 | 54 | 0 | 52 | ||

| мм | 31 | 62 | 32 | ||

| м/с2 | 1550 | 3100 | 1600 | ||
Угловые ускорения звеньев определяются на основе построенных планов ускорений.
Входное звено 1 вращается равномерно с постоянной угловой скоростью. Следовательно, его угловое ускорение равно нулю:
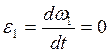
Модули угловых ускорений второго и четвертого звеньев для второго положения механизма можно найти по формулам:

Таблица 5. Значение угловых ускорений шатуна АВ и АВ' в с-2
| Обозначение | Единица | Положение механизма | ||
| 1 | 6 | 8 | ||
| ε 2 | с-2 | 8709 | 0 | 8387 |
| ε 4 | с-2 | 5000 | 10000 | 5161 |
Определим направления угловых ускорений звеньев 2 и 4. Чтобы определить направление углового ускорения ε 2 необходимо вектор относительного тангенциального ускорения  с плана ускорений перенести в точку В механизма, а точку А условно закрепить.
с плана ускорений перенести в точку В механизма, а точку А условно закрепить.
1.6 Построение диаграммы перемещения S ( t ), скорости υ ( t ) и ускорения a ( t ) точки В ползуна 3
По оси t откладываем отрезок L=240 мм. Данный отрезок соответствует времени оборота кривошипа.

Делим отрезок L на 12 равных частей и получаем точки 0, 1, …, 11, 12. Для построения диаграммы S(t) нужно из точек 0, 1, …, 11, 12 отложить ординаты, соответствующие перемещению точки В. Полученные точки 1', …, 11' соединяем плавной кривой.
Для построения диаграммы υ (t) воспользуемся методом дифференцирования (метод хорд). Криволинейные участки графика S(t), соответствующие интервалам оси t, заменяем хордами. Выбираем произвольной длинны полюсное расстояние Н1=36 мм. Из полюса P1 проводим лучи параллельные соответствующий хордам участков заданной кривой до пересечения с осью ординат. Из середины интервалов проводим перпендикуляры к оси абсцисс до пересечения с соответствующими линиями. Полученные точки 1'', …, 11'' соединяем плавной кривой.
Масштаб оси υ равен:
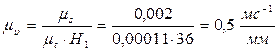
Диаграмму a(t) построим аналогичным способом (методом хорд) путем дифференцирования диаграммы υ (t). Выбираем произвольной длинны полюсное расстояние Н2=45 мм.
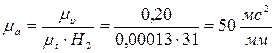
Лист №2
Последнее изменение этой страницы: 2019-04-09; Просмотров: 535; Нарушение авторского права страницы