Кинематика поступательного и вращательного движения.
План занятий.
1. Разбор вопросов студентов по домашнему заданию.
2. Решение типовых задач на доске.
3. Самостоятельное решение студентами некоторых задач на занятии и подведение итогов.
4. Формулировка домашнего задания.
Темы занятий.
1. Кинематика поступательного и вращательного движения. Тангенциальное и нормальное ускорение, радиус кривизны.
2. Динамика поступательного и вращательного движения.
3. Законы сохранения импульса, момента импульса и механической энергии
4. Контрольная работа из 4 задач по темам, рассмотренным на первых трех занятиях.
5. Механические колебания: собственные незатухающие и затухаюшие, вынужденные.
6. Идеальный газ: уравнение состояния, работа, внутренняя энергия, теплоемкость. Первое начало термодинамики.
7. Второе начало термодинамики. КПД тепловой машины. Распределения Максвелла и Больцмана.
8. Контрольная работа из 4 задач по темам, рассмотренным на 5-7 занятиях.
Занятие 1.
Кинематика поступательного и вращательного движения.
Тангенциальное и нормальное ускорение, радиус кривизны.
Положение частицы в пространстве определяется радиус-вектором 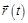 , который начинается в начале системы координат и заканчивается на частице.
, который начинается в начале системы координат и заканчивается на частице.
Скорость частицы 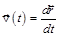 (перемещение за единицу времени). Кроме понятия скорости часто используют понятие средней скорости
(перемещение за единицу времени). Кроме понятия скорости часто используют понятие средней скорости 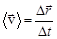 .
.
Ускорение частицы 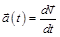 (изменение скорости за единицу времени)
(изменение скорости за единицу времени)
Для решения кинематических задач поступательного движения удобно пользоваться декартовой системой координат, в которой любой вектор можно разложить на три проекции вдоль осей х, y и z:
Радиус-вектор 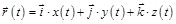 . (1.1,а)
. (1.1,а)
Скорость частицы 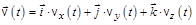 . (1.1,б)
. (1.1,б)
Ускорение частицы 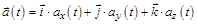 . (1.1,в)
. (1.1,в)
Здесь 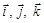 – единичные векторы (орты), направленные по осям
– единичные векторы (орты), направленные по осям 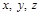 соответственно.
соответственно.
Прямая задача кинематики
Если известны зависимости 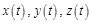 , то можно определить проекции скорости и ускорения на оси
, то можно определить проекции скорости и ускорения на оси 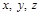 ,:
,:
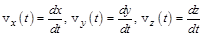 (1.2,а)
(1.2,а)
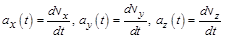 (1.2,б)
(1.2,б)
Величины (модули) векторов можно найти, используя теорему Пифагора: 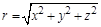 ;
; 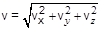 ;
; 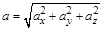 . (1.3)
. (1.3)
Обратная задача кинематики
Если известны зависимости 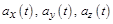 и начальные условия
и начальные условия 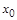 ,
, 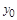 ,
, 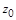 ,
, 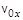 ,
, 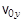 ,
, 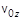 , то можно определить проекции скорости, а затем и координаты частицы в любой момент времени, т.е. определить закон ее движения:
, то можно определить проекции скорости, а затем и координаты частицы в любой момент времени, т.е. определить закон ее движения:
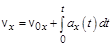 ;
; 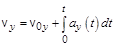 ;
; 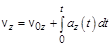 (1.4,а)
(1.4,а)
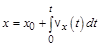 ;
; 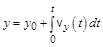 ;
; 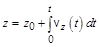 (1.4,б)
(1.4,б)
Величина перемещения частицы
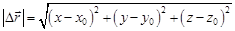 (1.4,в)
(1.4,в)
есть кратчайшее расстояние между начальным и конечным положением частицы в пространстве. Если движение частицы происходит не по прямой линии, то длина траектории, называемая путем, больше перемещения 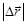 . Путь, пройденный частицей за время t:
. Путь, пройденный частицей за время t:
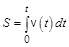 (1.5)
(1.5)
Качественные задачи.
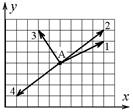 1.6к. Радиус-вектор частицы изменяется во времени по закону
1.6к. Радиус-вектор частицы изменяется во времени по закону 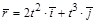 .
.
В момент времени t = 1 с частица оказалась в некоторой точке А. Выберите правильное направление скорости частицы в этот момент времени. а) 1; б) 2; в) 3; г) 4;
д) на рисунке нет правильного направления
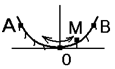 1.7к. Материальная точка M свободно без трения скользит в поле силы тяжести по гладким стенкам симметричной ямы (A и B – наивысшие точки подъема). При этом величина тангенциальной (касательной к траектории) проекции ускорения точки М:
1.7к. Материальная точка M свободно без трения скользит в поле силы тяжести по гладким стенкам симметричной ямы (A и B – наивысшие точки подъема). При этом величина тангенциальной (касательной к траектории) проекции ускорения точки М:
а) отлична от нуля в точке В;
б) максимальна в нижней точке траектории О;
в) равна нулю в точке А; г) одинакова во всех точках траектории;
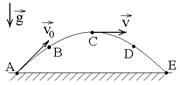 1.8к. Камень бросили под углом к горизонту со скоростью V0. Его траектория в однородном поле тяжести изображена на рисунке. Сопротивления воздуха нет. Модуль тангенциального ускорения
1.8к. Камень бросили под углом к горизонту со скоростью V0. Его траектория в однородном поле тяжести изображена на рисунке. Сопротивления воздуха нет. Модуль тангенциального ускорения 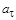 на участке А-В-С:
на участке А-В-С:
1) уменьшается 2) увеличивается 3) не изменяется
1.9к. Тело брошено с поверхности Земли со скоростью 10 м/с под углом 45° к горизонту. Если сопротивлением воздуха пренебречь и принять g = 10 м/с2, то радиус кривизны траектории в верхней точке (в метрах) равен .....
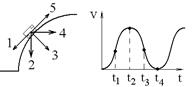 1.10к. Из-за неисправности мотора величина скорости автомобиля синусоидально изменялась во времени, как показано на графике зависимости V(t). В момент времени t1 автомобиль поднимался по участку дуги. Куда может быть направлена результирующая всех сил, действующих на автомобиль в этот момент времени?
1.10к. Из-за неисправности мотора величина скорости автомобиля синусоидально изменялась во времени, как показано на графике зависимости V(t). В момент времени t1 автомобиль поднимался по участку дуги. Куда может быть направлена результирующая всех сил, действующих на автомобиль в этот момент времени?
1) 1 2) 2 3) 3 4) 4 5) 5
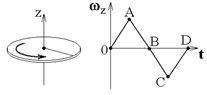 1.11к. Диск вращается вокруг своей оси, изменяя проекцию своей угловой скорости так, как показано на рисунке. На каких участках графика зависимости
1.11к. Диск вращается вокруг своей оси, изменяя проекцию своей угловой скорости так, как показано на рисунке. На каких участках графика зависимости 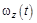 вектор угловой скорости
вектор угловой скорости 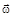 и вектор углового ускорения
и вектор углового ускорения 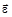 направлены в одну сторону? 1) 0 - А и А-В 2) 0 -А и В - С 3) В - С и С - D
направлены в одну сторону? 1) 0 - А и А-В 2) 0 -А и В - С 3) В - С и С - D
4) всегда направлены в одну сторону
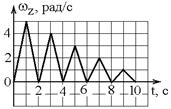 1.12к. Твердое тело начинает вращаться вокруг оси Z с угловой скоростью, проекция которой изменяется во времени, как показано на графике. В какой момент времени угол поворота тела относительно начального положения будет максимальным?
1.12к. Твердое тело начинает вращаться вокруг оси Z с угловой скоростью, проекция которой изменяется во времени, как показано на графике. В какой момент времени угол поворота тела относительно начального положения будет максимальным?
а) 10 с б) 1 с в) 2 с г) 9 с
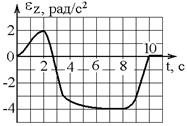 1.13к. Диск радиуса R начинает вращаться из состояния покоя в горизонтальной плоскости вокруг оси Z, проходящей перпендикулярно его плоскости через его центр. Зависимость проекции углового ускорения от времени показана на графике. Во сколько раз отличаются величины тангенциальных ускорений точки на краю диска в моменты времени t1 = 2 с и t2 = 7 с?
1.13к. Диск радиуса R начинает вращаться из состояния покоя в горизонтальной плоскости вокруг оси Z, проходящей перпендикулярно его плоскости через его центр. Зависимость проекции углового ускорения от времени показана на графике. Во сколько раз отличаются величины тангенциальных ускорений точки на краю диска в моменты времени t1 = 2 с и t2 = 7 с?
а) в 2 раза б) в 4 раза в) оба равны нулю г) трудно определить точно
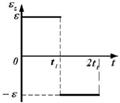 1.14к. Твердое тело начинает вращаться вокруг оси Z. Зависимость углового ускорения
1.14к. Твердое тело начинает вращаться вокруг оси Z. Зависимость углового ускорения 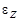 от времени представлена на графике. Соответствующая зависимость угловой скорости
от времени представлена на графике. Соответствующая зависимость угловой скорости 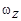 от времени представлена графиком ...
от времени представлена графиком ...
а) 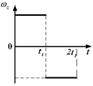 б)
б) 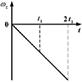 в)
в) 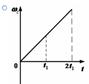 г)
г) 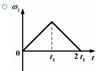
1.15к. Прямолинейное движение точки описывается уравнением 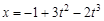 (в единицах СИ). Средняя скорость точки за время движения до остановки в м/с равна ....
(в единицах СИ). Средняя скорость точки за время движения до остановки в м/с равна ....
Задачи для самостоятельной работы.
1.1с. Радиус-вектор частицы зависит от времени по закону
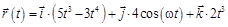 . Через сколько секунд перпендикулярной оси х окажется а) скорость частицы; б) ускорение частицы
. Через сколько секунд перпендикулярной оси х окажется а) скорость частицы; б) ускорение частицы
1.2с. Частица начала свое движение из точки с радиусом-вектором 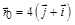 (м), со скоростью, которая зависит от времени по закону
(м), со скоростью, которая зависит от времени по закону 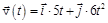 (м/с). На какое расстояние от начала координат удалится частица в момент времени
(м/с). На какое расстояние от начала координат удалится частица в момент времени 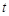 = 4 с.
= 4 с.
 1.3с. Равнозамедленно вращающийся шкив повернулся на угол
1.3с. Равнозамедленно вращающийся шкив повернулся на угол 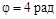 к тому моменту, когда его угловая скорость уменьшилась в три раза. Найти величину углового ускорения шкива. Его начальная скорость
к тому моменту, когда его угловая скорость уменьшилась в три раза. Найти величину углового ускорения шкива. Его начальная скорость 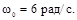
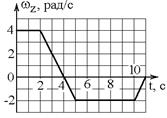
1.4с. Твердое тело начинает вращаться вокруг оси Z с угловой скоростью, проекция которой изменяется во времени, как показано на графике. На какой угол относительно начального положения окажется повернутым тело через 11 секунд?
а) 8 рад б) 12 рад в) 24 рад г) 0 рад
1.5с.. Частица движется вдоль окружности с радиусом 1 м в соответствии с уравнением 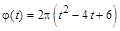 , где
, где 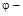 угол в радианах,
угол в радианах, 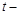 время в секундах. Величина нормального ускорения частицы равна нулю в момент времени (в секундах), равный: а) 1, б) 2, в) 3, г) 4
время в секундах. Величина нормального ускорения частицы равна нулю в момент времени (в секундах), равный: а) 1, б) 2, в) 3, г) 4
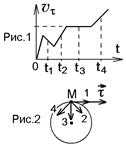 1.6с. Материальная точка M движется по окружности со скоростью
1.6с. Материальная точка M движется по окружности со скоростью 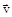 . На рис.1 показан график зависимости проекции скорости
. На рис.1 показан график зависимости проекции скорости 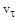 на орт
на орт 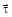 , направленный вдоль скорости
, направленный вдоль скорости 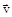 . На рис.2 укажите направление силы, действующей на точку M в момент времени t1:
. На рис.2 укажите направление силы, действующей на точку M в момент времени t1:
а) 1
б) 2
в) 3
г) 4
Занятие 2
Качественные задачи.
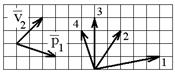 2.7к. Импульс тела
2.7к. Импульс тела 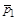 изменился под действием короткого удара и скорость тела стала равной
изменился под действием короткого удара и скорость тела стала равной 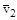 , как показано на рисунке. В каком направлении могла действовать сила?
, как показано на рисунке. В каком направлении могла действовать сила?
а) 2, 3, 4 б) 1 в) только 4 г) 1, 2
 2.8к. Теннисный мяч летел с импульсом
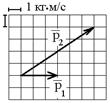
2.8к. Теннисный мяч летел с импульсом 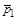 в горизонтальном направлении, когда теннисист произвел по мячу резкий удар длительностью
в горизонтальном направлении, когда теннисист произвел по мячу резкий удар длительностью 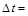 0,1 с. Изменившийся импульс мяча стал равным
0,1 с. Изменившийся импульс мяча стал равным 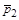 (масштаб указан на рисунке). Найти среднюю силу удара. а)30 Н б) 5 Н в) 50 Н
(масштаб указан на рисунке). Найти среднюю силу удара. а)30 Н б) 5 Н в) 50 Н
г) 0,5 Н д) 0,1 Н
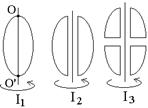 2.9к. Из жести вырезали три одинаковые детали в виде эллипса. Две детали разрезали: одну - пополам вдоль оси симметрии, а вторую - на четыре одинаковые части. Затем все части отодвинули друг от друга на одинаковое расстояние и расставили симметрично относительно оси OO' (см. рис.). Выберите правильное соотношение между моментами инерции этих деталей относительно оси OO'.
2.9к. Из жести вырезали три одинаковые детали в виде эллипса. Две детали разрезали: одну - пополам вдоль оси симметрии, а вторую - на четыре одинаковые части. Затем все части отодвинули друг от друга на одинаковое расстояние и расставили симметрично относительно оси OO' (см. рис.). Выберите правильное соотношение между моментами инерции этих деталей относительно оси OO'.
а) 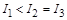 б)
б) 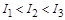 в)
в) 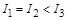 г)
г) 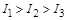
2.10к. На барабан радиусом R = 0,5 м намотан шнур, к концу которого привязан груз массой m = 10 кг. Груз опускается с ускорением a = 2 м/с2. Момент инерции барабана равен ...
2.11к. Обруч, раскрученный в вертикальной плоскости и посланный по полу рукой гимнастки, через несколько секунд сам возвращается к ней. Начальная скорость центра обруча равна 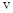 = 10 м/с, коэффициент трения между обручем и полом равен m = 0,5. Максимальное расстояние, на которое откатывается обруч от гимнастки, равно ...
= 10 м/с, коэффициент трения между обручем и полом равен m = 0,5. Максимальное расстояние, на которое откатывается обруч от гимнастки, равно ...
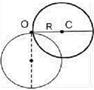 2.12к. Тонкий обруч радиусом 1 м, способный свободно вращаться вокруг горизонтальной оси, проходящей через точку О перпендикулярно плоскости рисунка, отклонили от вертикали на угол 90° и отпустили. В начальный момент времени угловое ускорение обруча равно ... а) 20 с–2 б) 7 с–2 в) 5 с–2 г) 10 с–2
2.12к. Тонкий обруч радиусом 1 м, способный свободно вращаться вокруг горизонтальной оси, проходящей через точку О перпендикулярно плоскости рисунка, отклонили от вертикали на угол 90° и отпустили. В начальный момент времени угловое ускорение обруча равно ... а) 20 с–2 б) 7 с–2 в) 5 с–2 г) 10 с–2
2.13к. Зависимость импульса частицы от времени описывается законом 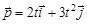 , где
, где 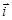 и
и 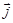 – единичные векторы координатных осей Х, Y соответственно. Зависимость горизонтальной проекции силы
– единичные векторы координатных осей Х, Y соответственно. Зависимость горизонтальной проекции силы 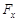 , действующей на частицу, от времени представлена на графике ...
, действующей на частицу, от времени представлена на графике ...
а) 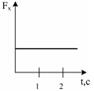 б)
б) 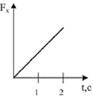 в)
в) 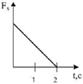 г)
г) 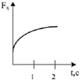
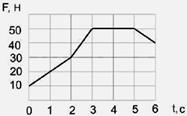 2.14к. На графике показана зависимость силы, действующей на тело, от времени. За первые три секунды импульс тела изменился на ...
2.14к. На графике показана зависимость силы, действующей на тело, от времени. За первые три секунды импульс тела изменился на ...
а) 80 Н×с
б) 300 Н×с
в) 150 Н×с
г) 50 Н×с
2.15к. При выстреле орудия снаряд вылетел из ствола с угловой скоростью w = 200 с–1 под углом a =60° к горизонту. Момент инерции снаряда относительно его продольной оси I = 15 кг×м2, растояние между колесами орудия 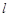 = 1,5 м, время движения снаряда в стволе
= 1,5 м, время движения снаряда в стволе 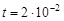 с. Силы давления (в килоньютонах) земли, действующие на колеса во время выстрела, отличаются на ...
с. Силы давления (в килоньютонах) земли, действующие на колеса во время выстрела, отличаются на ...
 Задачи для самостоятельной работы.
Задачи для самостоятельной работы.
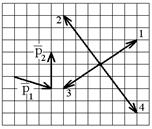
2.1с. Импульс тела 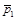 изменился под действием короткого удара и стал равным
изменился под действием короткого удара и стал равным 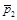 , как показано на рисунке. В каком направлении действовала сила?
, как показано на рисунке. В каком направлении действовала сила?
а) 1
 б) 2
б) 2
в) 3
г) 4
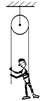
2.2с. Через невесомый блок перекинут невесомый шнур, к концу которого привязан человек массы m = 60 кг. С какой силой человек должен тянуть за другой конец шнура, чтобы подниматься вверх?
 2.3с. Теннисный мяч летел с импульсом
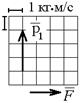
2.3с. Теннисный мяч летел с импульсом 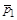 (масштаб и направление указаны на рисунке). В перпендикулярном направлении на короткое время
(масштаб и направление указаны на рисунке). В перпендикулярном направлении на короткое время 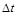 = 0,1 с на мяч подействовал порыв ветра с постоянной силой F = 40 Н. Какова стала величина импульса p2 после того, как ветер утих? а) 5 кг×м/с б) 0,5 кг×м/с в) 43 кг×м/с
= 0,1 с на мяч подействовал порыв ветра с постоянной силой F = 40 Н. Какова стала величина импульса p2 после того, как ветер утих? а) 5 кг×м/с б) 0,5 кг×м/с в) 43 кг×м/с
г) 50 кг×м/с д) 7 кг×м/с
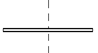 2.4с. Найти угловую скорость, с которой начал вращаться вокруг вертикальной закреплённой оси тонкий стержень массы m = 200 г и длины l = 80 см, лежащий на горизонтальной плоскости. Ось проходит через середину стержня, и в оси вращения возникает постоянный момент сил трения M тр= 0,15 H . Повернувшись на угол
2.4с. Найти угловую скорость, с которой начал вращаться вокруг вертикальной закреплённой оси тонкий стержень массы m = 200 г и длины l = 80 см, лежащий на горизонтальной плоскости. Ось проходит через середину стержня, и в оси вращения возникает постоянный момент сил трения M тр= 0,15 H . Повернувшись на угол 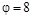 рад, стержень останавливается.
рад, стержень останавливается.
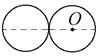 2.5с.. Два одинаковых диска массой m = 1 кг и радиусом R = 1 м каждый положили на плоскость и приварили друг к другу. Найти момент инерции получившейся детали относительно оси, проходящей перпендикулярно плоскости дисков через центр масс одного из дисков О.
2.5с.. Два одинаковых диска массой m = 1 кг и радиусом R = 1 м каждый положили на плоскость и приварили друг к другу. Найти момент инерции получившейся детали относительно оси, проходящей перпендикулярно плоскости дисков через центр масс одного из дисков О.
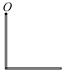 2.6с. Два одинаковых однородных тонких стержня массой m = 1 кг и длиной l = 1 м каждый приварили концами перпендикулярно друг к другу. Через конец одного из стержней проходит ось О, перпендикулярная плоскости стержней. Найти момент инерции получившейся детали относительно оси О.
2.6с. Два одинаковых однородных тонких стержня массой m = 1 кг и длиной l = 1 м каждый приварили концами перпендикулярно друг к другу. Через конец одного из стержней проходит ось О, перпендикулярная плоскости стержней. Найти момент инерции получившейся детали относительно оси О.
 2.7с. Тонкий однородный стержень массы m= 1 кг и длины l = 1 м может вращаться в горизонтальной плоскости без трения вокруг вертикальной оси С, проходящей через середину стержня. К концу стержня в плоскости вращения под углом a = 30° к стержню прикладывают силу
2.7с. Тонкий однородный стержень массы m= 1 кг и длины l = 1 м может вращаться в горизонтальной плоскости без трения вокруг вертикальной оси С, проходящей через середину стержня. К концу стержня в плоскости вращения под углом a = 30° к стержню прикладывают силу 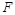 =1 Н. Найдите угловое ускорение стержня в начальный момент времени.
=1 Н. Найдите угловое ускорение стержня в начальный момент времени.
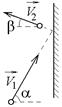 2.8с. Небольшой шарик массы m = 1 кг летит со скоростью
2.8с. Небольшой шарик массы m = 1 кг летит со скоростью 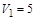 м/с под углом a = 60° к горизонту и падает на вертикальную стену. После неупругого удара он отскакивает со скоростью
м/с под углом a = 60° к горизонту и падает на вертикальную стену. После неупругого удара он отскакивает со скоростью 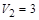 м/с под углом b =30° к горизонту. Время соударения t = 0,001 с. Найти модуль средней силы нормальной реакции со стороны стены.
м/с под углом b =30° к горизонту. Время соударения t = 0,001 с. Найти модуль средней силы нормальной реакции со стороны стены.
Занятие 3
И механической энергии
Исходя из закона изменения импульса (2.1), можно рассмотреть частный случай, когда сумма внешних сил равна нулю. Тогда импульс системы не изменяется во времени (закон сохранения импульса):
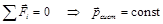 (3.1)
(3.1)
Исходя из закона изменения момента импульса (2.3), можно рассмотреть частный случай, когда сумма внешних моментов сил равна нулю. Тогда момент импульс системы не изменяется во времени (закон сохранения момента импульса):
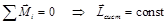 (3.2)
(3.2)
Очень часто в физических задачах рассматривается модель очень краткого взаимодействия двух или нескольких тел (столкновение двух тел в полете, взрыв сняряда и разлет осколков, столкновение свободного тела с телом, подвешенным на шарнире, и т.д.). Если в таких ситуациях результирующая сила или момент сил за время столкновения не существенно изменяют импульс (2.2) или момент импульса (2.4), то законы (3.1) и (3.2) можно считать почти точными.
В случаях существенного изменения импульса или момента импульса остается возможность применения законов сохранения (3.1) и (3.2) только в проекции на ось, проекция результирующей силы или момента силы на которую равны нулю:
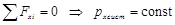 (3.3)
(3.3)
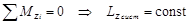 (3.4)
(3.4)
Третьим основным законом механики является закон изменения полной механической энергии системы 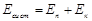 , где
, где 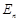 – потенциальная энергия системы тел,
– потенциальная энергия системы тел, 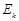 – кинетическая энергия этой системы:
– кинетическая энергия этой системы:
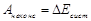 , (3.5)
, (3.5)
где 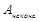 – работа неконсервативных сил.
– работа неконсервативных сил.
Если работа неконсервативных сил равна нулю, то выполняется закон сохранения механической энергии:
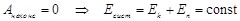 (3.6)
(3.6)
В механических задачах чаще всего учитываются два типа потенциальных энергий и два типа кинетических.
Гравитационная потенциальная энергия и потенциальная энергия упругой деформации
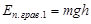 или
или 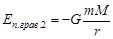
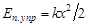 (3.7)
(3.7)
где 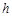 – высота центра масс тела над произвольным нулевым уровнем,
– высота центра масс тела над произвольным нулевым уровнем, 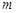 – масса тела,
– масса тела, 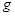 – ускорение свободного падения,
– ускорение свободного падения, 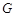 – гравитационная постоянная,
– гравитационная постоянная, 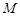 – масса планеты,
– масса планеты,  – расстояние от центра планеты до центра масс тела,
– расстояние от центра планеты до центра масс тела, 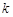 – коэффициент жесткости пружины,
– коэффициент жесткости пружины, 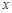 – деформация пружины.
– деформация пружины.
Понятие потенциальной энергии связано с выделением особых консервативных сил. Связь между консервативной силой и потенциальной энергией задается оператором "набла", действие которого на скалярную функцию 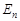 называется градиентом потенциальной энергии:
называется градиентом потенциальной энергии:
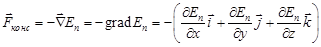 , (3.8)
, (3.8)
Кинетическая энергия поступательного и вращательного движения
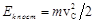 ,
, 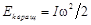 (3.9)
(3.9)
где 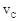 – скорость центра масс системы тел с суммарной массой
– скорость центра масс системы тел с суммарной массой 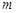 ,
,
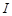 – момент инерции системы тел относительно оси вращения (2.5), проходящей через центр масс С этой системы, w – угловая скорость вращения вокруг этой оси (чаще всего для системы из одного вращающегося тела).
– момент инерции системы тел относительно оси вращения (2.5), проходящей через центр масс С этой системы, w – угловая скорость вращения вокруг этой оси (чаще всего для системы из одного вращающегося тела).
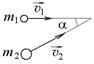 3.1. Маленький пластилиновый шарик массы m1 = 0,1 кг движется горизонтально со скоростью
3.1. Маленький пластилиновый шарик массы m1 = 0,1 кг движется горизонтально со скоростью 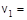 1 м/с. Под углом a = 30° к направлению его движения летит второй шарик массы m2 = 0,2 кг со скоростью
1 м/с. Под углом a = 30° к направлению его движения летит второй шарик массы m2 = 0,2 кг со скоростью 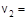 2 м/с и сталкивается с первым. Шарики слипаются и движутся под углом b к первоначальному направлению движения первого шарика. Найдите
2 м/с и сталкивается с первым. Шарики слипаются и движутся под углом b к первоначальному направлению движения первого шарика. Найдите 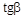 . Ответ: 0,448
. Ответ: 0,448
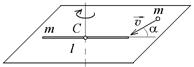 3.2. На горизонтальной плоскости лежит тонкий однородный стержень массы m =0,1 кг и длины l = 1 м, который может вращаться вокруг вертикальной оси, проходящей через центр масс стержня С. Под углом a =30° к стержню в той же плоскости движется маленький пластилиновый шарик такой же массы m со скоростью
3.2. На горизонтальной плоскости лежит тонкий однородный стержень массы m =0,1 кг и длины l = 1 м, который может вращаться вокруг вертикальной оси, проходящей через центр масс стержня С. Под углом a =30° к стержню в той же плоскости движется маленький пластилиновый шарик такой же массы m со скоростью 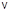 = 1 м/с. Шарик прилипает к концу стержня, и система приобретает угловую скорость вращения w. Найти угловую скорость вращения системы после удара. Ответ: 0,75 рад/с.
= 1 м/с. Шарик прилипает к концу стержня, и система приобретает угловую скорость вращения w. Найти угловую скорость вращения системы после удара. Ответ: 0,75 рад/с.
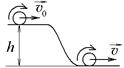 3.3. Тонкий однородный диск массы m = 1 кг и радиуса R = 1 м скатывается без проскальзывания с горки высоты h = 1 м, совершая плоское движение. Начальная скорость центра масс диска равна
3.3. Тонкий однородный диск массы m = 1 кг и радиуса R = 1 м скатывается без проскальзывания с горки высоты h = 1 м, совершая плоское движение. Начальная скорость центра масс диска равна 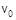 = 1 м/с. Сопротивление воздуха пренебрежимо мало, g = 10 м/с2. Найдите скорость центра масс диска , после того, как он скатится с горки. Ответ: 3,79 м/с;
= 1 м/с. Сопротивление воздуха пренебрежимо мало, g = 10 м/с2. Найдите скорость центра масс диска , после того, как он скатится с горки. Ответ: 3,79 м/с;
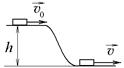 3.4. Резиновая шайба массы m = 1 кг, двигаясь со скоростью
3.4. Резиновая шайба массы m = 1 кг, двигаясь со скоростью 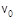 = 1 м/с, соскальзывает с горки высоты h = 1 м и приобретает скорость
= 1 м/с, соскальзывает с горки высоты h = 1 м и приобретает скорость 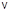 у подножия горки. Во время движения над шайбой была совершена работа сил трения, модуль которой равен Атр=1 Дж (g = 10 м/с2). Найдите скорость шайбы
у подножия горки. Во время движения над шайбой была совершена работа сил трения, модуль которой равен Атр=1 Дж (g = 10 м/с2). Найдите скорость шайбы 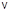 Ответ: 4,36 м/с
Ответ: 4,36 м/с
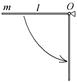 3.5. Тонкий однородный стержень массы m = 1 кг и длины l = 1 м может вращаться в вертикальной плоскости вокруг горизонтальной оси, проходящей через конец стержня О. Стержень приводят в горизонтальное положение и отпускают без толчка. Сопротивление воздуха пренебрежимо мало, g = 10 м/с2. В момент прохождения им положения равновесия найдите скорость нижнего конца стержня. (5,48 м/с)
3.5. Тонкий однородный стержень массы m = 1 кг и длины l = 1 м может вращаться в вертикальной плоскости вокруг горизонтальной оси, проходящей через конец стержня О. Стержень приводят в горизонтальное положение и отпускают без толчка. Сопротивление воздуха пренебрежимо мало, g = 10 м/с2. В момент прохождения им положения равновесия найдите скорость нижнего конца стержня. (5,48 м/с)
Качественные задачи.
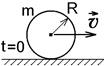 3.6к.. В начальный момент времени t = 0 тонкий обруч с массой m = 0,1 кг и с радиусом R = 0,5 м не вращался, а поступательно скользил по горизонтальной поверхности с кинетической энергией 800 Дж. Под действием силы трения он начал катиться без проскальзывания с кинетической энергией поступательного движения 200 Дж. Сила трения совершила работу:
3.6к.. В начальный момент времени t = 0 тонкий обруч с массой m = 0,1 кг и с радиусом R = 0,5 м не вращался, а поступательно скользил по горизонтальной поверхности с кинетической энергией 800 Дж. Под действием силы трения он начал катиться без проскальзывания с кинетической энергией поступательного движения 200 Дж. Сила трения совершила работу:
а) 300 Дж б) 600 Дж в) 500 Дж г) 400 Дж
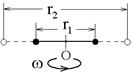 3.7к. Два маленьких массивных шарика закреплены на невесомом длинном стержне на расстоянии r1 друг от друга. Стержень может вращаться без трения в горизонтальной плоскости вокруг вертикальной оси, проходящей посередине между шариками. Стержень раскрутили из состояния покоя до угловой скорости w, при этом была совершена работа А1. Шарики раздвинули симметрично на расстояние r2 = 2r1 и раскрутили до той же угловой скорости. Какая работа при этом была совершена?
3.7к. Два маленьких массивных шарика закреплены на невесомом длинном стержне на расстоянии r1 друг от друга. Стержень может вращаться без трения в горизонтальной плоскости вокруг вертикальной оси, проходящей посередине между шариками. Стержень раскрутили из состояния покоя до угловой скорости w, при этом была совершена работа А1. Шарики раздвинули симметрично на расстояние r2 = 2r1 и раскрутили до той же угловой скорости. Какая работа при этом была совершена?
1) А2 = 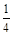 А1 2) А2 = 2А1 3) А2 =
А1 2) А2 = 2А1 3) А2 = 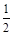 А1 4) А2 = 4А1
А1 4) А2 = 4А1
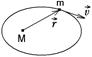 3.8к. Планета массой
3.8к. Планета массой 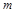 движется по эллиптической орбите, в одном из фокусов которой находится звезда массы
движется по эллиптической орбите, в одном из фокусов которой находится звезда массы 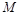 .
. 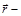 радиус-вектор планеты (см.рисунок). Выберите правильное утверждение:
радиус-вектор планеты (см.рисунок). Выберите правильное утверждение:
а) момент импульса планеты относительно центра звезды меняется и максимален при наибольшем ее удалении 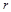 от звезды
от звезды
б) момент силы тяготения, действующей на планету (относительно центра звезды), изменяется, но направлен перпендикулярно плоскости орбиты
в) величина момента импульса планеты относительно центра звезды в любой момент времени определяется выражением 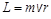
г) момент импульса планеты относительно центра звезды не изменяется
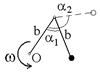 3.9к. Два невесомых стержня длины b соединены под углом a1 = 60° и вращаются без трения в горизонтальной плоскости вокруг вертикальной оси О с угловой скоростью w. На конце одного из стержней прикреплен очень маленький массивный шарик. В некоторый момент угол между стержнями самопроизвольно увеличился до a2 = 120°. С какой угловой скоростью стала вращаться такая система? 1) 3w 2)
3.9к. Два невесомых стержня длины b соединены под углом a1 = 60° и вращаются без трения в горизонтальной плоскости вокруг вертикальной оси О с угловой скоростью w. На конце одного из стержней прикреплен очень маленький массивный шарик. В некоторый момент угол между стержнями самопроизвольно увеличился до a2 = 120°. С какой угловой скоростью стала вращаться такая система? 1) 3w 2) 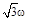 3)
3) 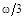 4)
4) 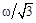 5) w
5) w
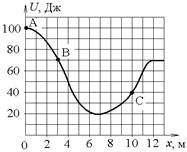 3.10к. Небольшая шайба начинает движение без начальной скорости по гладкой ледяной горке из точки А. Сопротивление воздуха пренебрежимо мало. Зависимость потенциальной энергии шайбы от координаты х изображена на графике
3.10к. Небольшая шайба начинает движение без начальной скорости по гладкой ледяной горке из точки А. Сопротивление воздуха пренебрежимо мало. Зависимость потенциальной энергии шайбы от координаты х изображена на графике 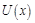 . Кинетическая энергия шайбы в точке С
. Кинетическая энергия шайбы в точке С
а) в 2 раза больше, чем в точке В
б) в 2 раза меньше, чем в точке В
в) в 1,75 раза больше, чем в точке В г)в 1,75 раза меньше, чем в точке В
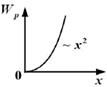 3.11к. На рисунке показан график зависимости потенциальной энергии
3.11к. На рисунке показан график зависимости потенциальной энергии 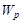 от координаты х. График зависимости проекции силы
от координаты х. График зависимости проекции силы 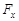 от координаты х имеет вид ...
от координаты х имеет вид ...
а)  б)
б) 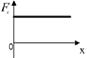 в)
в) 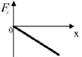 г)
г) 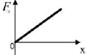
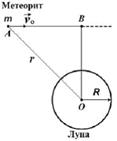 3.12к. Находясь на расстоянии
3.12к. Находясь на расстоянии 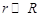 , по направлению к Луне летит метеорит, скорость которого
, по направлению к Луне летит метеорит, скорость которого 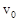 . Для расчета минимального прицельного расстояния ОВ, при котором метеорит не упадет на поверхность Луны, используют законы сохранения механической энергии и момента импульса. Выберите из предложенных вариантов верную запись этих законов . Радиус
. Для расчета минимального прицельного расстояния ОВ, при котором метеорит не упадет на поверхность Луны, используют законы сохранения механической энергии и момента импульса. Выберите из предложенных вариантов верную запись этих законов . Радиус 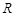 и массу
и массу 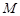 Луны, гравитационную постоянную
Луны, гравитационную постоянную 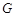 , скорость метеорита вблизи поверхности Луны
, скорость метеорита вблизи поверхности Луны 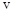 считать известными.
считать известными.
а) 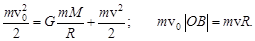
б) 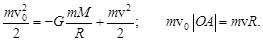
в) 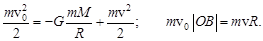
3.13к. Кинетическая энергия тела (спутника), движущегося по круговой орбите вокруг Земли, меньше его гравитационной потенциальной энергии, взятой по модулю в ______ раза.
3.14к. Шарик массой 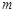 упал с высоты
упал с высоты 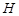 на стальную плиту и упруго отскочил от нее вверх. Изменение импульса шарика в результате удара равно ...
на стальную плиту и упруго отскочил от нее вверх. Изменение импульса шарика в результате удара равно ...
а) 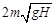 б)
б) 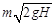 в)
в) 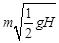 г)
г) 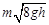
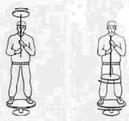 3.15к. Экспериментатор, стоящий на неподвижной скамье Жуковского, получает от помощника колесо, вращающееся вокруг вертикальной оси с угловой скоростью w. Если экспериментатор повернет ось вращения колеса на угол 180°, то он вместе с платформой придет во вращение с угловой скоростью w/5. Отношение момента инерции экспериментатора со скамьей к моменту инерции колеса равно ... а) 10 б) 2,5 в) 5 г) 4
3.15к. Экспериментатор, стоящий на неподвижной скамье Жуковского, получает от помощника колесо, вращающееся вокруг вертикальной оси с угловой скоростью w. Если экспериментатор повернет ось вращения колеса на угол 180°, то он вместе с платформой придет во вращение с угловой скоростью w/5. Отношение момента инерции экспериментатора со скамьей к моменту инерции колеса равно ... а) 10 б) 2,5 в) 5 г) 4
Задачи для самостоятельной работы.
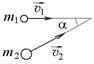 3.1с. Маленький пластилиновый шарик массы m1 = 0,1 кг движется горизонтально со скоростью
3.1с. Маленький пластилиновый шарик массы m1 = 0,1 кг движется горизонтально со скоростью 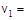 1 м/с. Под углом a = 45° к направлению его движения летит второй шарик массы m2 = 0,2 кг со скоростью
1 м/с. Под углом a = 45° к направлению его движения летит второй шарик массы m2 = 0,2 кг со скоростью 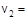 2 м/с и сталкивается с первым. Шарики слипаются и движутся под углом b к первоначальному направлению движения второго шарика. Найдите
2 м/с и сталкивается с первым. Шарики слипаются и движутся под углом b к первоначальному направлению движения второго шарика. Найдите 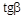 .
.
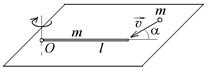 3.2с. На горизонтальной плоскости лежит тонкий однородный стержень массы m =0,1 кг и длины l = 1 м, который может вращаться вокруг вертикальной оси, проходящей через конец стержня О. Под углом a =30° к стержню в той же плоскости движется маленький пластилиновый шарик такой же массы m со скоростью
3.2с. На горизонтальной плоскости лежит тонкий однородный стержень массы m =0,1 кг и длины l = 1 м, который может вращаться вокруг вертикальной оси, проходящей через конец стержня О. Под углом a =30° к стержню в той же плоскости движется маленький пластилиновый шарик такой же массы m со скоростью 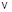 = 1 м/с. Шарик прилипает к концу стержня, и система приобретает угловую скорость вращения w. Найти угловую скорость вращения системы после удара
= 1 м/с. Шарик прилипает к концу стержня, и система приобретает угловую скорость вращения w. Найти угловую скорость вращения системы после удара
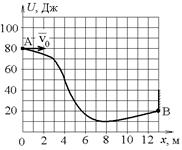 3.3с. Тело массы m = 10 кг начинает движение со скоростью
3.3с. Тело массы m = 10 кг начинает движение со скоростью 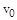 = 4 м/с по гладкой ледяной горке из точки А. Сопротивление воздуха пренебрежимо мало. Зависимость потенциальной энергии этого тела от координаты х изображена на графике
= 4 м/с по гладкой ледяной горке из точки А. Сопротивление воздуха пренебрежимо мало. Зависимость потенциальной энергии этого тела от координаты х изображена на графике 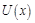 . В точке В тело, ударившись, прилипает к стене. Сколько теплоты выделилось в результате абсолютно неупругого удара в точке В?
. В точке В тело, ударившись, прилипает к стене. Сколько теплоты выделилось в результате абсолютно неупругого удара в точке В?
а) 140 Дж б) 160 Дж в) 20 Дж г) 150 Дж
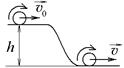 3.4с. Однородный шар массы m = 1 кг и радиуса R = 1 м скатывается без проскальзывания с горки высоты h = 1 м. Начальная скорость центра масс шара равна
3.4с. Однородный шар массы m = 1 кг и радиуса R = 1 м скатывается без проскальзывания с горки высоты h = 1 м. Начальная скорость центра масс шара равна 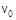 = 1 м/с. Сопротивление воздуха пренебрежимо мало, g = 10 м/с2. Найдите кинетическую энергию шара, после того, как он скатится с горки
= 1 м/с. Сопротивление воздуха пренебрежимо мало, g = 10 м/с2. Найдите кинетическую энергию шара, после того, как он скатится с горки
 3.5с. Тонкий однородный стальной стержень массы m = 1 кг и длины l = 1 м может вращаться в вертикальной плоскости вокруг горизонтальной оси, проходящей через его конец O. Горизонтально в той же плоскости на стержень налетает стальной шарик той же массы m со скоростью
3.5с. Тонкий однородный стальной стержень массы m = 1 кг и длины l = 1 м может вращаться в вертикальной плоскости вокруг горизонтальной оси, проходящей через его конец O. Горизонтально в той же плоскости на стержень налетает стальной шарик той же массы m со скоростью 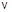 = 1 м/с и отскакивает со скоростью u после абсолютно упругого удара. Стержень начинает вращаться с угловой скоростью w = 1 рад/с. Найти скорость шарика u.
= 1 м/с и отскакивает со скоростью u после абсолютно упругого удара. Стержень начинает вращаться с угловой скоростью w = 1 рад/с. Найти скорость шарика u.
Занятие 4
Механические колебания:
Занятие 5
Занятие 6
Качественные задачи
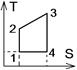 6.7к. На рисунке представлен прямой цикл тепловой машины в координатах
6.7к. На рисунке представлен прямой цикл тепловой машины в координатах 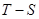 , где
, где 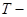 термодинамическая температура,
термодинамическая температура, 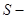 энтропия. Укажите участки, на которых тепло поступает в рабочее тело машины от нагревателей, и участки, где тепло отдается холодильнику:
энтропия. Укажите участки, на которых тепло поступает в рабочее тело машины от нагревателей, и участки, где тепло отдается холодильнику:
а) 12, 23 – поступает; 41 – отдается б) 23 – поступает; 41 – отдается
в) 12, 23 – поступает; 34, 41 – отдается г) 12 – поступает; 34 – отдается
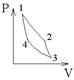 6.8к. Идеальная тепловая машина работает по циклу Карно (две изотермы 1-2 и 3-4 и две адиабаты 2-3 и 4-1). Как изменится энтропия рабочего тела в процессе изотермического расширения 1-2?
6.8к. Идеальная тепловая машина работает по циклу Карно (две изотермы 1-2 и 3-4 и две адиабаты 2-3 и 4-1). Как изменится энтропия рабочего тела в процессе изотермического расширения 1-2?
1) энтропия возрастет
2) энтропия уменьшится 3) энтропия не изменится
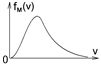 6.9к. На рисунке представлен график распределения молекул идеального газа по величинам скоростей (распределение Максвелла). С ростом температуры
6.9к. На рисунке представлен график распределения молекул идеального газа по величинам скоростей (распределение Максвелла). С ростом температуры 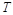 газа площадь под этим графиком будет:
газа площадь под этим графиком будет:
а) оставаться неизменной б) расти пропорционально 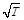
в) расти пропорционально 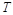 г) расти пропорционально
г) расти пропорционально 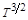
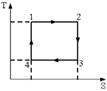 6.10к. На рисунке изображен цикл Карно в координатах (Т, S), где S – энтропия. Адиабатное расширение происходит на этапе ...
6.10к. На рисунке изображен цикл Карно в координатах (Т, S), где S – энтропия. Адиабатное расширение происходит на этапе ...
а) 3 – 4 б) 4 – 1 в) 2 – 3 г) 1 – 2
6.11к. Если количество теплоты, отдаваемое рабочим телом холодильнику, увеличится в два раза, то коэффициент полезного действия тепловой машины...
а) уменьшится на 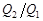 ; б) увеличится на
; б) увеличится на 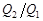 ;
;
в) увеличится на 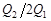 ; г) уменьшится на
; г) уменьшится на 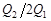
6.12к. Зависимость концентрации молекул идеального газа во внешнем однородном поле силы тяжести от высоты для двух разных температур 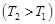 представлена на рисунке ...
представлена на рисунке ...
а) 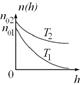 б)
б) 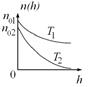 в)
в) 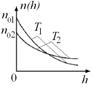 г)
г) 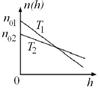
6.12к. Зависимость давления идеального газа во внешнем однородном поле силы тяжести от высоты для двух разных температур 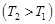 представлена на рисунке ...
представлена на рисунке ...
а) 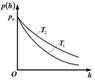 б)
б) 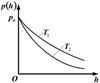 в)
в) 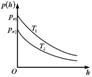 г)
г) 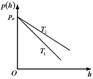
Задачи для самостоятельной работы.
6.1с. Два моля азота сначала изобарически нагревают в два раза, а затем изотермически сжимают в два раза. Найти суммарное изменение энтропии в этих двух процессах.
6.2с. Машина, работающая по циклу Карно, совершает за цикл работу в три раза меньшую, чем отдаваемое за цикл тепло. Найти температуру холодильника, если температура нагревателя t н0 = 99 0 С.
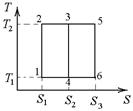 6.3с. Первая тепловая машина совершает циклический процесс 1–2–3–4–1, а вторая 4–3–5–6–4 (см. график). На сколько процентов больше коэффициент полезного действия второй тепловой машины. Принять T1 = 300 К;
6.3с. Первая тепловая машина совершает циклический процесс 1–2–3–4–1, а вторая 4–3–5–6–4 (см. график). На сколько процентов больше коэффициент полезного действия второй тепловой машины. Принять T1 = 300 К; 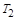 = 600 К.
= 600 К.
S1 = 1 Дж/К; S2 = 2 Дж/К; S3 = 3 Дж/К.
6.4с. Идеальный газ находился в закрытом сосуде, а средняя квадратичная скорость молекул была равна 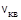 =500 м/с. Потом газ был нагрет так, что средняя скорость молекул стала равна
=500 м/с. Потом газ был нагрет так, что средняя скорость молекул стала равна 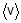 =470 м/с. Найти: отношение частоты ударов молекул о единичную площадку во втором и в первом состояниях
=470 м/с. Найти: отношение частоты ударов молекул о единичную площадку во втором и в первом состояниях 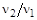 .
.
6.5с. На берегу моря атмосферное давление составляет 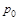 , а температура воздуха
, а температура воздуха 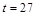 °С одинакова на разных высотах. Молярная масса воздуха m = 29 г/моль. Универсальная газовая постоянная
°С одинакова на разных высотах. Молярная масса воздуха m = 29 г/моль. Универсальная газовая постоянная 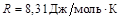 , g = 10 м/с2. Если подняться на высоту Н =1 км над уровнем моря, то во сколько раз уменьшится давление p?
, g = 10 м/с2. Если подняться на высоту Н =1 км над уровнем моря, то во сколько раз уменьшится давление p?
План занятий.
1. Разбор вопросов студентов по домашнему заданию.
2. Решение типовых задач на доске.
3. Самостоятельное решение студентами некоторых задач на занятии и подведение итогов.
4. Формулировка домашнего задания.
Темы занятий.
1. Кинематика поступательного и вращательного движения. Тангенциальное и нормальное ускорение, радиус кривизны.
2. Динамика поступательного и вращательного движения.
3. Законы сохранения импульса, момента импульса и механической энергии
4. Контрольная работа из 4 задач по темам, рассмотренным на первых трех занятиях.
5. Механические колебания: собственные незатухающие и затухаюшие, вынужденные.
6. Идеальный газ: уравнение состояния, работа, внутренняя энергия, теплоемкость. Первое начало термодинамики.
7. Второе начало термодинамики. КПД тепловой машины. Распределения Максвелла и Больцмана.
8. Контрольная работа из 4 задач по темам, рассмотренным на 5-7 занятиях.
Занятие 1.
Кинематика поступательного и вращательного движения.

