
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
ЧЕРНІГІВСЬКИЙ НАЦІОНАЛЬНИЙ ТЕХНОЛОГІЧНИЙ УНІВЕРСИТЕТСтр 1 из 10Следующая ⇒
ЧЕРНІГІВСЬКИЙ НАЦІОНАЛЬНИЙ ТЕХНОЛОГІЧНИЙ УНІВЕРСИТЕТ КОЛЕДЖ транспорту та комп’ютерних технологій ЗАТВЕРДЖУЮ Голова методичної ради _____________ В.М. Радченко «___» _____2015р. МЕТОДИЧНИЙ ПОСІБНИК до практичних занять із дисципліни «Комп'ютерна логіка» для студентів спеціальності 5.05010201 „Обслуговування комп’ютерних систем і мереж” СХВАЛЕНО Протокол засідання циклової комісії «___» ____ 2015р. №___
2015 рік ЗМІСТ
ПОЯСНЮВАЛЬНА ЗАПИСКА До програми курсу „Комп'ютерна електроніка” входить виконання практичних робіт. Після виконання практичних робіт студенти повинні: - навчитися аналізувати схеми поширених електронних пристроїв, розрізняти умовні позначення застосованих радіоелементів; - знати методику розрахунку параметрів основних електронних пристроїв: підсилювачів, автогенераторів, логічних елементів, тригерів, регістрів, лічильників; - мати уявлення про можливості використання напівпровідникових приладів, інтегральних мікросхем при рішенні певних практичних задач. Практичні роботи проводяться поетапно після вивчення відповідного теоретичного матеріалу. Наведені в кожній практичній роботі теоретичні відомості або методики розрахунку охоплюють необхідний для підготовки і виконання роботи мінімум навчального матеріалу. Крім того, практична робота передбачає виконання індивідуального завдання. Завдання включає в себе розрахунок параметрів, режимів роботи електронних пристроїв, методи побудови цифрових схем та аналізу їх роботи.
ВИТЯГ ІЗ РОБОЧОЇ ПРОГРАМИ ТЕМИ ПРАКТИЧНИХ ЗАНЯТЬ
ІІ семестр (8 годин) | |||||||||||||||||||||||||||||||||||
| 1 | 3 | 2.1 Системи числення. Перетворення двійкової інформації | 2-2 | Системи числення. Перетворення чисел у числа інших систем числення | |||||||||||||||||||||||||||||||
| 2 | 4 | 2.1 Системи числення. Перетворення двійкової інформації | 2-4 | Системи числення. Двійкова арифметика | |||||||||||||||||||||||||||||||
| 3 | 9 | 2.4 Дії з числами в арифметико-логічних пристроях | 2-6 | Дії з числами в арифметично-логічних пристроях. Додавання і віднімання двійкових чисел | |||||||||||||||||||||||||||||||
| 4 | 10 | 2.4 Дії з числами в арифметико-логічних пристроях | 2-8 | Дії з числами в арифметично-логічних пристроях. Множення і ділення двійкових чисел | |||||||||||||||||||||||||||||||
|
ІІІ семестр (8 годин) | |||||||||||||||||||||||||||||||||||
| 5 | 22 | 5.2 Синтез логічних пристроїв у заданому базисі | 2-2 | Спрощення логічних виразів | |||||||||||||||||||||||||||||||
| 6 | 23 | 5.2 Синтез логічних пристроїв у заданому базисі | 2-4 | Мінімізація логічних рівнянь | |||||||||||||||||||||||||||||||
| 7 | 24 | 5.2 Синтез логічних пристроїв у заданому базисі | 2-6 | Синтез логічних пристроїв у заданому базисі | |||||||||||||||||||||||||||||||
| 8 | 27 | 4.3 Мультиплексори. Шифратори. Дешифратори. Суматори. Компаратори. Перетворювачі кодів | 2-8 | Будова комбінаційних схем у заданому базисі | |||||||||||||||||||||||||||||||
ПЕРЕЛІК ПОСИЛАНЬ
1 Гуржій А.М. Імпульсна та цифрова техніка : підручник для учнів професійно- технічних навчальних закладів / А.М.Гуржій, В.В.Самсонов, Н.І.Поворознюк. – Х. : ТОВ «Компанія СМІТ», 2005. – 424 с.
2 Калабеков Б.А. Цифровые устройства и микропроцессорные системы / Б.А. Калабеков. - М. : Горячая линия - Телеком, 2002. – 336 с.
3 Колонтаєвський Ю.П. Електроніка і мікросхемотехніка / Ю.П.Колонтаєвський, А.Г.Сосков. - К. : Каравела, 2012. – 416 с.
4 Локазюк В.М. Мікропроцесори та мікроЕОМ у виробничих системах: Посібник / В.М. Локазюк. – К.: Видавничий центр «Академія», 2007. – 368 с.
5 Партала О.Н. Цифровая электроника: Учебник для техникумов / О.Н.Партала. - М.: «Наука и техника», 2000. – 297 с.
6 Рябенький В.М. Цифрова схемотехніка / В.М. Рябенький, В.Я. Жуйков. – Львів : Новий світ, 2009. - 736 с.
7 Семененко В.А. Арифметико-логические основы комп'ютерной схемотехники: Учебное пособие для высшей школы / В.А. Семененко. – М.: Академический проект, 2004. – 144 с.
8 Сенько В.І. Електроніка і мікросхемотехніка: Підручник / В.І.Сенько, М.В.Панасенко. – К.: «Каравела», 2008. – 400 с.
ЗМІСТ ПРАКТИЧНИХ ЗАНЯТЬ
МЕТА:
- навчальна: вчити перетворювати числа з однієї системи числення в іншу;
- розвиваюча: розвивати вміння працювати за зразком і вказівками викладача, самостійно застосовувати знання до вирішення практичних завдань;
- виховна: виховувати увагу, логічне мислення, впевненість у вирішенні практичних завдань:
ОБЛАДНАННЯ: калькулятор, ручка
ПЛАН
1 Позиційні та непозиційні системи числення.
2 Десяткова, двійкова, вісімкова, шістнадцяткова системи числення.
3 Перетворення чисел у числа інших систем числення. Двійкова арифметика.
4 Двійково-десяткова система числення. Спеціальні системи числення.
5 Системи числення з від'ємною основою.
ЗМІСТ ПРАКТИЧНОГО ЗАНЯТТЯ
За індивідуальним варіантом завдання треба:
- уважно ознайомиться з завданням;
- представити десяткові числа в двійковій, вісімковій, шістнадцятковій і двійково-десятковій системах числення;
- представити двійкові числа в десятковій системі числення;
- представити вісімкові числа в десятковій системі числення;
- представити шістнадцяткові числа в десятковій системі числення;
- представити десяткові дробові числа в десятковій системі числення.
Варіанти завдань:
1 Представити десяткові числа в двійковій, вісімковій, шістнадцятковій і двійково-десятковій системах числення:
| № варіанта | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| Число | 58 | 85 | 67 | 127 | 59 | 42 | 78 | 81 | 69 | 59 | 70 | 27 | 63 | 17 | 39 |
| № варіанта | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| Число | 48 | 75 | 37 | 17 | 49 | 92 | 88 | 82 | 40 | 51 | 65 | 28 | 61 | 60 | 20 |
2. Представити двійкові числа в десятковій системі числення:
| № варіанта | 1 | 2 | 3 | 4 | 5 | 6 |
| Число | 1001100011 | 1010101011 | 1111100111 | 1101101110 | 1010111011 | 1011101111 |
| № варіанта | 7 | 8 | 9 | 10 | 11 | 12 |
| Число | 1011100001 | 1010101001 | 1110100111 | 1100101110 | 1011111011 | 1010101111 |
| № варіанта | 13 | 14 | 15 | 16 | 17 | 18 |
| Число | 1000100011 | 1010101111 | 1111100111 | 1101101010 | 1010101011 | 1011001111 |
| № варіанта | 19 | 20 | 21 | 22 | 23 | 24 |
| Число | 1001110011 | 1010111011 | 1101100111 | 1101101010 | 1010011011 | 1001101011 |
| № варіанта | 25 | 26 | 27 | 28 | 29 | 30 |
| Число | 1001100011 | 1010101001 | 1101100111 | 1001101110 | 1010111001 | 1011101110 |
3. Представити вісімкові числа в десятковій системі числення:
| № варіанта | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| Число | 57 | 75 | 67 | 17 | 53 | 42 | 71 | 45 | 32 | 16 | 70 | 27 | 63 | 13 | 31 |
|
| |||||||||||||||
| № варіанта | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| Число | 44 | 74 | 37 | 15 | 42 | 22 | 55 | 52 | 40 | 51 | 65 | 25 | 61 | 60 | 20 |
МЕТА:
- навчальна: вчити виконувати арифметичні дії в різних системах числення;
- розвиваюча: розвивати вміння працювати за зразком і вказівками викладача, самостійно застосовувати знання до вирішення практичних завдань;
- виховна: виховувати увагу, логічне мислення, впевненість у вирішенні практичних завдань:
ОБЛАДНАННЯ: калькулятор, ручка
ПЛАН
3 Позиційні та непозиційні системи числення.
4 Десяткова, двійкова, вісімкова, шістнадцяткова системи числення.
3 Перетворення чисел у числа інших систем числення. Двійкова арифметика.
4 Двійково-десяткова система числення. Спеціальні системи числення.
5 Системи числення з від'ємною основою.
ЗМІСТ ПРАКТИЧНОГО ЗАНЯТТЯ
За індивідуальним варіантом завдання треба:
- уважно ознайомиться з завданням.
- виконати арифметичні дії з числами, представленими в двійковій системі числення - додавання, віднімання.
Варіанти завдань:
Варіант 1
1 Виконати арифметичні операції над двійковим числом Х1 = 101111 і Х2 = 110
а) додавання б) віднімання в) множення г) ділення.
2 Виконати арифметичні дії з двійковими числами:
а) 11011101 + 10101110 б) 11011 – 110 в) 1011∙ 1011.
3 Додати числа 16 і 3 у десятковій, двійковій, с.ч.
4 Помножити числа 12 і 6 у десятковій, двійковій с.ч
5 Розділити числа20 і 7 у десятковій, двійковій с.ч
6 Знайдемо різницю між числами 55 і 7 у десятковій, двійковій с.ч.
7 Задані двійкові числа X і Y. Вичислити X+Y і X-Y , якщо: X=1101001; Y=101111.
8 Задані двійкові числа X і Y. Вичислити X*Y і X/Y , якщо: X=1000010011; Y=1011.
9 Виконати складання наступних двійкових чисел: 10112+01012
10 Виконати віднімання наступних двійкових чисел: 10112-01012 .
11 Додати два двійкових числа 1101+0001.
12 Перемножити два числа: 1012·112
13 Розділити два числа: 11112:112.
14 Відніміти:
а) 1112 із 101002 б) 158 із 208 в) 1А16 із 3116.
15 Перемножити числа:
а)1011012 і 1012 б)378 і 48.
16 Додайте числа:
а) 10111012 та 11101112 б) 378 и 758 в) A16 и F16.
Варіант 2
1 Виконати арифметичні операції над двійковим числом Х1 = 111101 і Х2 = 1010
а) додавання б) віднімання в) множення г) ділення.
2 Виконати арифметичні дії з двійковими числами:
а) 110101 + 1010110 б) 11011 – 100 в) 1001∙ 1011.
3 Додати числа 7 і 6 у десятковій, двійковій, с.ч.
4 Помножити числа 11 і 5 у десятковій, двійковій с.ч
5 Розділити числа10 і 4 у десятковій, двійковій с.ч
6 Знайдемо різницю між числами 25 і 4 у десятковій, двійковій с.ч.
7 Задані двійкові числа X і Y. Вичислити X+Y і X-Y , якщо: X=100011001; Y=101011.
8 Задані двійкові числа X і Y. Вичислити X*Y і X/Y , якщо: X=110010101; Y=1001.
9 Виконати складання наступних двійкових чисел: 11012+00112.
10 Виконати віднімання наступних двійкових чисел: 11012+00112.
11 Додати два двійкових числа 1101+0001.
12 Перемножити два числа: 1012·112
13 Розділити два числа: 11112:112.
14 Відніміть:
а) 1112 із 101002 б) 158 із 208 в) 1А16 із 3116.
15 Перемножити числа:
а) 1111012 і 11,012 б) 168 і 78.
16 Додайте числа:
а) 1011,1012 і 101,0112 б) 1658 і 378 в) 1916 і C16.
Варіант 3
1 Виконати арифметичні операції над двійковим числом Х1 = 100101 і Х2 =10111
а) додавання б) віднімання в) множення г) ділення.
2 Виконати арифметичні дії з двійковими числами:
а) 1101101 + 10101010 б) 1011 – 110 в) 1011∙ 101.
3 Додати числа 13 і 6 у десятковій, двійковій, с.ч.
4 Помножити числа 22 і 5 у десятковій, двійковій с.ч
5 Розділити числа 7 і 6 у десятковій, двійковій с.ч
6 Знайдемо різницю між числами 40 і 8 у десятковій, двійковій с.ч.
7 Задані двійкові числа X і Y. Вичислити X+Y і X-Y , якщо: X=100011001; Y=101011.
8 Задані двійкові числа X і Y. Вичислити X*Y і X/Y , якщо: X=100101.011; Y=110.1.
9 Виконати складання наступних двійкових чисел: 10012+11002.
10 Виконати віднімання наступних двійкових чисел: 10012+11002.
11 Додати два двійкових числа 1101+0001.
12 Перемножити два числа: 1012·112
13 Розділити два числа: 11102:102.
14 Відніміть:
а) 111,12 із 100102 б) 56,78 із 1018 в) B,9216 із D,116.
15 Перемножити числа:
а) 1011,112 і 101,12 б) 7,58 і 1,68.
16 Додайте числа:
а) 10112, 112 і 111,12 б) 7,58 і 14,68 в) A,B16 і E,F16.
Варіант 4
1 Виконати арифметичні операції над двійковим числом Х1 = 110011 і Х2 = 110 1
а) додавання б) віднімання в) множення г) ділення.
2 Виконати арифметичні дії з двійковими числами:
а) 1101101 + 1010110 б) 1011 – 111 в) 10001∙ 1001.
3 Додати числа 33 і 5 у десятковій, двійковій, с.ч.
4 Помножити числа 42 і 7 у десятковій, двійковій с.ч
5 Розділити числа 7 і 3 у десятковій, двійковій с.ч
6 Знайдемо різницю між числами 41 і 6 у десятковій, двійковій с.ч.
7 Задані двійкові числа X і Y. Вичислити X+Y і X-Y , якщо: X=1101001; Y=101111.
8 Задані двійкові числа X і Y. Вичислити X*Y і X/Y , якщо: X=100000.1101; Y=101.01.
9 Виконати складання наступних двійкових чисел: 10112+01012.
10 Виконати віднімання наступних двійкових чисел: 10112+01012.
11 Додати два двійкових числа 1101+0001.
12 Перемножити два числа: 1102·0112
13 Розділити два числа: 11112:112.
14 Відніміть:
а) 1110,112 із 100012 б) 16,548 із 30,018 в) ABC16 із 567816.
15 Перемножити числа:
а) 1012 і 1111,0012 б) 6,258 і 7,128.
16 Додайте числа:
а) 10112 , 11,12 і 1112 б) 68, 178 і 78 в) E16, 916 і F16.
ЗАКРІПЛЕННЯ ВИВЧЕНОГО І ОЦІНЮВАННЯ РІВНЯ ЗНАНЬ: перевірка і оцінювання за рівнем повноти і правильності визначення основних показників підсилювального каскаду
ДОМАШНЄ ЗАВДАННЯ: самостійно вирішити наступні завдання:
1 Виконати арифметичні операції над двійковим числом Х1 = 110111 і Х2 = 1012
а) додавання б) віднімання в) множення г) ділення.
2 Виконати арифметичні дії з двійковими числами
а) 1111001 + 101001 б) 1111 – 101 в) 101∙ 111.
3 Додати числа 27 і 7 у десятковій, двійковій с.ч.
4 Помножити числа 22 і 6 у десятковій, двійковій с.ч
5 Розділити числа 20 і 6 у десятковій, двійковій с.ч
6 Знайдемо різницю між числами 31 і 5 у десятковій, двійковій с.ч
7 Задани двійкові числа X і Y. Вичислити X+Y і X-Y , якщо: X=100011001; Y=101011.
8 Задани двійкові числа X і Y. Вичислити X*Y і X/Y , якщо: X=1000010011; Y=1011.
9 Запишіть в кодах Грея числа
а)310 б)210; в)610.
10 Виконати складання наступних двійкових чисел 10112+01012 .
11 Виконати віднімання наступних двійкових чисел 10112-01012 .
12 Додати два двійкових числа 01012+00012.
13 Перемножити два числа 1102·1012.
14 Розділити два числа 11102:102.
15 Віднімить:
а) 1112 из 101002; б) 158 из 208 в) 1А16 из 3116.
16 Перемножьте числа
а) 1011012 и 1012; б) 378 и 48
17 Додайте числа
а) 10111112 и 11101012; б) 178 и 658; в) СA16 и F16.
18 Переведіть число із двійкової системи у вісімкову і шістнадцятиричну: 1001111110111,01112.
ВИКЛАДАЧ –Т.І.Ковальова
МЕТА:
- навчальна: вчити виконувати арифметичні дії в в арифметично-логічних пристроях;
- розвиваюча: розвивати вміння працювати за зразком і вказівками викладача, самостійно застосовувати знання до вирішення практичних завдань;
- виховна: виховати увагу, логічне мислення, впевненість у вирішенні практичних завдань:
ОБЛАДНАННЯ: калькулятор, ручка
ПЛАН
1 Дії з числами в арифметично-логічних пристроях.
2 Складання та віднімання двійкових чисел з фіксованою та плаваючою комою.
3 Множення двійкових чисел.
4 Складання двійкових чисел в зворотному та додатковому кодах. Операція множення в додатковому коді.
ЗМІСТ ПРАКТИЧНОГО ЗАНЯТТЯ
За індивідуальним варіантом завдання треба:
- уважно ознайомиться з завданням.
- виконати арифметичні дії з двійковими числами з фіксованою та плаваючою комою;
- виконати складання двійкових чисел в зворотному та додатковому кодах в арифметично-логічних пристроях.
- виконати складання двійкових чисел у модифікованому коді.
Варіанти завдань:
Варіант 1
1 Виконати арифметичні операції над цілими числами Х1 = -11002 і Х2 = +01112, представлених у формі з фіксованою точкою
а) додавання б) віднімання.
2 Записати, як буде представлено в АЛП десяткове число -31 в прямому, зворотному, додатковому кодах
3 Запишіть ряд чисел +3, +2, ..., -3 , що зменшуються, в однобайтовому форматі
а) в прямому коді б) в зворотному коді в) в додатковому коді.
4 Запишіть числа в прямому коді (формат 1 байт)
а) 21 б) -63.
5 Запишіть числа в зворотному і додатковому кодах (формат 1 байт)
а) -9 б) -15.
6 Знайдіть десяткові представлення чисел, записаних в додатковому коді
а) 1 1111000 б) 1 0011011 в) 1 1101001 г) 1 0000000.
7 Знайдіть десяткові представлення чисел, записаних в зворотному коді:
а) 1 1101000 б) 1 0011111 в) 1 0101011 г) 1 0000000.
8 Виконаєте віднімання чисел шляхом додавання їх зворотних кодів в форматі 1 байт. Вкажіть, в яких випадках має місце переповнювання розрядної сітці:
| а) 9 – 2 б) 2 - 9 в) -5 - 7 г) -2-10. |
9 Виконаєте віднімання чисел шляхом додавання їх додаткових кодів в форматі 1 байт. Вкажіть, в яких випадках має місце переповнювання розрядної сітці:
| а) 9 – 2 б) 2 – 9 в) -5 – 7 г) -20-10. |
10 Додати два трьохрозрядних числа, представлених в додатковому коді:
а) 1101+0001 б) 0101+0001.
11 Число 100101 представлено в додатковому коді як п'ятирозрядне. Представити його в двійковій системі числення.
12 Число 00010101 представлено в двійково-десятковому коді. Представити його в десятковій системі числення.
Варіант 2
1 Виконати арифметичні операції над цілими числами Х1 = -01102 і Х2 = +00112, представлених у формі з фіксованою точкою
а) додавання б) віднімання.
2 Записати, як буде представлено в АЛП десяткове число -56 в прямому, зворотному, додатковому кодах
3 Запишіть ряд чисел +2, ..., -4 , що зменшуються, в однобайтовому форматі
а) в прямому коді б) в зворотному коді в) в додатковому коді.
4 Запишіть числа в прямому коді (формат 1 байт)
а) 23 б) -7.
5 Запишіть числа в зворотному і додатковому кодах (формат 1 байт)
а) -8 б) -17
6 Знайдіть десяткові представлення чисел, записаних в додатковому коді
а) 1 0011001 б) 1 0010011 в) 1 0101001 г) 1 00000110
7 Знайдіть десяткові представлення чисел, записаних в зворотному коді:
а) 1 0011001 б) 1 0010011 в) 1 0101001 г) 1 00000110
8 Виконаєте віднімання чисел шляхом додавання їх зворотних кодів в форматі 1 байт. Вкажіть, в яких випадках має місце переповнювання розрядної сітці:
| а) 8 - 2 б) 2 - 8 в) -6 - 8 г) -30 - 20 |
9 Виконаєте віднімання чисел шляхом додавання їх додаткових кодів в форматі 1 байт. Вкажіть, в яких випадках має місце переповнювання розрядної сітці:
| а) 8 - 2 б) 2 - 8 в) -6 - 8 г) -30 - 20 |
10 Додати два трьохрозрядних числа, представлених в додатковому коді
а) 1001+0011 б) 0111+0101
11 Число 100101 представлено в додатковому коді як п'ятирозрядне. Представити його в двійковій системі числення.
12 Число 101101 представлено в двійково-десятковому коді. Представити його в десятковій системі числення.
Варіант 3
1 Виконати арифметичні операції над цілими числами Х1 = +11002 і Х2 = -10102, представлених у формі з фіксованою точкою
а) додавання б) віднімання.
2 Записати, як буде представлено в АЛП десяткове число -48 в прямому, зворотному, додатковому кодах
3 Запишіть ряд чисел +4, ..., -2 , що зменшуються, в однобайтовому форматі
а) в прямому коді б) в зворотному коді в) в додатковому коді.
4 Запишіть числа в прямому коді (формат 1 байт)
а) 13 б) -9.
5 Запишіть числа в зворотному і додатковому кодах (формат 1 байт)
а) -6 б) -27
6 Знайдіть десяткові представлення чисел, записаних в додатковому коді
а) 1 1011001 б) 1 0110011 в) 1 0101101 г) 1 0100011
7 Знайдіть десяткові представлення чисел, записаних в зворотному коді:
а) 1 1011001 б) 1 0110011 в) 1 0101101 г) 1 0100011
8 Виконаєте віднімання чисел шляхом додавання їх зворотних кодів в форматі 1 байт. Вкажіть, в яких випадках має місце переповнювання розрядної сітці:
| а) 6 - 2 б) 2 - 6 в) -5 - 8 г) -18-9 |
9 Виконаєте віднімання чисел шляхом додавання їх додаткових кодів в форматі 1 байт. Вкажіть, в яких випадках має місце переповнювання розрядної сітці:
| а) 6 - 2 б) 2 - 6 в) -5 - 8 г) -18-9 |
10 Додати два трьохрозрядних числа, представлених в додатковому коді
а) 1101+0011 б) 0101+0101
11 Число 101111 представлено в додатковому коді як п'ятирозрядне. Представити його в двійковій системі числення.
12 Число 101111 представлено в двійково-десятковому коді. Представити його в десятковій системі числення.
Варіант 4
1 Виконати арифметичні операції над цілими числами Х1 = +1012 і Х2 = -1112, представлених у формі з фіксованою точкою
а) додавання б) віднімання.
2 Записати, як буде представлено в АЛП десяткове число -38 в прямому, зворотному, додатковому кодах
3 Запишіть ряд чисел +3, ..., -1 , що зменшуються, в однобайтовому форматі
а) в прямому коді б) в зворотному коді в) в додатковому коді.
4 Запишіть числа в прямому коді (формат 1 байт)
а) 19 б) -4.
5 Запишіть числа в зворотному і додатковому кодах (формат 1 байт)
а) -22 б) -3
6 Знайдіть десяткові представлення чисел, записаних в додатковому коді
а) 1 1100101 б) 1 0110010 в) 1 0010101 г) 1 0100100
7 Знайдіть десяткові представлення чисел, записаних в зворотному коді:
а) 1 1100101 б) 1 0110010 в) 1 0010101 г) 1 0100100
8 Виконаєте віднімання чисел шляхом додавання їх зворотних кодів в форматі 1 байт. Вкажіть, в яких випадках має місце переповнювання розрядної сітці:
| а) 10 - 4 б) 4 - 10 в) -3 - 9 г) -25-5 |
9 Виконаєте віднімання чисел шляхом додавання їх додаткових кодів в форматі 1 байт. Вкажіть, в яких випадках має місце переповнювання розрядної сітці:
| а) 10 - 4 б) 4 - 10 в) -3 - 9 г) -25-5 |
10 Додати два трьохрозрядних числа, представлених в додатковому коді
а) 10111+ 10110 б) 1101+0101
11 Число 101011 представлено в додатковому коді як п'ятирозрядне. Представити його в двійковій системі числення.
12 Число 0111010011 представлено в двійково-десятковому коді. Представити його в десятковій системі числення.
Варіант 5
1 Виконати арифметичні операції над цілими числами Х1 = +1102 і Х2 = -0112, представлених у формі з фіксованою точкою
а) додавання б) віднімання.
2 Записати, як буде представлено в АЛП десяткове число -18 в прямому, зворотному, додатковому кодах
3 Запишіть ряд чисел +1, ..., -5 , що зменшуються, в однобайтовому форматі
а) в прямому коді б) в зворотному коді в) в додатковому коді.
4 Запишіть числа в прямому коді (формат 1 байт)
а) 29 б) -14.
5 Запишіть числа в зворотному і додатковому кодах (формат 1 байт)
а) -12 б) -5
6 Знайдіть десяткові представлення чисел, записаних в додатковому коді
а) 1 1000101 б) 1 0010010 в) 1 0010001 г) 1 0100110
7 Знайдіть десяткові представлення чисел, записаних в зворотному коді:
а) 1 1000101 б) 1 0010010 в) 1 0010001 г) 1 0100110
8 Виконаєте віднімання чисел шляхом додавання їх зворотних кодів в форматі 1 байт. Вкажіть, в яких випадках має місце переповнювання розрядної сітці:
| а) 11 - 5 б) 5 - 11 в) -3 - 7 г) -15-4 |
9 Виконаєте віднімання чисел шляхом додавання їх додаткових кодів в форматі 1 байт. Вкажіть, в яких випадках має місце переповнювання розрядної сітці:
| а) 11 - 5 б) 5 - 11 в) -3 - 7 г) -15-4 |
10 Додати два трьохрозрядних числа, представлених в додатковому коді
а) 11010+ 1111 б) 0101+0111
11 Число 101001 представлено в додатковому коді як п'ятирозрядне. Представити його в двійковій системі числення.
12 Число 110111010001 представлено в двійково-десятковому коді. Представити його в десятковій системі числення.
ЗАКРІПЛЕННЯ ВИВЧЕНОГО І ОЦІНЮВАННЯ РІВНЯ ЗНАНЬ: перевірка і оцінювання за рівнем повноти і правильності аналізу схеми та визначення опорів резисторів за постійним струмом підсилювального каскаду
ДОМАШНЄ ЗАВДАННЯ: самостійно вирішити наступні завдання:
1 Записати число в прямому, зворотному й додатковому кодах
а) 11010 б) -11101 в) -101001 г) -1001110
2 Перевести X і Y у прямий, зворотний і додатковий коди. Скласти їх у зворотному й додатковому кодах. Результат перевести в прямий код. Перевірити отриманий результат, користуючись правилами двійкової арифметики.
| а) X= -11010; Y= 1001111; | б) X= -11101; Y= -100110; | в) X= 1110100; Y= -101101; |
| г) X= -10110; Y= -111011; | д) X= 1111011; Y= -1001010; | е) X= -11011; Y= -10101. |
3 Скласти X і Y у модифікованому зворотному й модифікованому додатковому восьмиразрядных кодах. У випадку появи ознаки переповнення збільшити число розрядів у кодах і повторити підсумовування. Результат перевести в прямий код і перевірити, користуючись правилами двійкової арифметики.
| а) X= 10110; Y= 110101; | б) X= 11110; Y= -111001; | в) X= -11010; Y= -100111; |
| г) X= -11001; Y=-100011; | д) X= -10101; Y= 111010; | е) X= -1101; Y= -111011. |
ВИКЛАДАЧ –Т.І.Ковальова
МЕТА:
- навчальна: вчити виконувати арифметичні дії в в арифметично-логічних пристроях;
- розвиваюча: розвивати вміння працювати за зразком і вказівками викладача, самостійно застосовувати знання до вирішення практичних завдань;
- виховна: виховати увагу, логічне мислення, впевненість у вирішенні практичних завдань:
ОБЛАДНАННЯ: ручка
ПЛАН
1 Дії з числами в арифметично-логічних пристроях.
2 Складання та віднімання двійкових чисел з фіксованою та плаваючою комою.
3 Множення двійкових чисел.
4 Складання двійкових чисел в зворотному та додатковому кодах. Операція множення в додатковому коді.
5 Ділення двійкових чисел з поновленням та без поновлення залишків.
6 Представлення в нормалізованому виді двійкових чисел.
ЗМІСТ ПРАКТИЧНОГО ЗАНЯТТЯ
За індивідуальним варіантом завдання треба:
- уважно ознайомиться з завданням;
- виконати арифметичні дії з двійковими числами з фіксованою та плаваючою комою;
- виконати множення і ділення двійкових чисел в зворотному та додатковому кодах в арифметично-логічних пристроях.
Варіанти завдань:
Варіант 1
1 Записати в нормалізованому вигляді наступне двійкове число: 100111.101
2 Як буде представлено десяткове число 8,25 в двійковому вигляді в розрядній сітці в формі з плаваючою комою (32 розряди, з них 7 розрядів – порядок числа) ?

3 Записати, як буде представлено в АЛП десяткове число -31 в прямому, зворотному, додатковому кодах
4 Знайдіть десятковий еквівалент числа представленого в додатковому коді: 0.10111
5 Виконати множення над цілими числами Х1 = -11002 і Х2 = +01112, представлених у формі з фіксованою точкою.
6 Додати двійкові нормалізовані числа А = 0,10101 • 2-1 і В= 0,10001 • 210.
7 Виконати віднімання двійкових нормалізованих чисел А = 0,10101 • 210 і В= 0,10001 • 21.
8 Виконати множення двійкових нормалізованих чисел А= 0,101 • 2101 і В= 0,110 • 211.
9 Додати двійкові числа у модифікованому додатковому коді Х1 = -11002 і Х2 = +01112,
10 Виконати ділення двійкових нормалізованих чисел А = 0,10101 • 210 і В= 0,10001 • 21.
11 Виконати додавання в АЛП двох десяткових чисел А= 8 і В=9.
12 Записати десяткове число 51 в двійково – десятковій системі числення.
13 Представити десяткове число А = 0,00078 • 106 в нормалізованій формі.
14 Перетворити десяткове число 54 за схемою (10 с.ч.) → (2 с.ч.) → (8 с.ч.) → (10 с.ч.)
Варіант 2
1 Записати в нормалізованому вигляді наступне двійкове число: 1101.10101
2 Як буде представлено десяткове число 6,43 в двійковому вигляді в розрядній сітці в формі з плаваючою комою (32 розряди, з них 7 розрядів – порядок числа) ?

3 Записати, як буде представлено в АЛП десяткове число -56 в прямому, зворотному, додатковому кодах
4 Знайдіть десятковий еквівалент числа представленого в додатковому коді: 0.101001
5 Виконати множення над цілими числами Х1 = -01102 і Х2 = +00112, представлених у формі з фіксованою точкою
6 Додати двійкові нормалізовані числа А = 0,1001 • 21 і В= 0,1011 • 211 .
7 Виконати віднімання двійкових нормалізованих чисел А = 0,1001 • 211 і В= 0,1011 • 210 .
8 Виконати множення двійкових нормалізованих чисел А= 0,111 • 2110 і В= 0,110 • 2101.
9 Додати двійкові числа у модифікованому додатковому коді Х1 = -01102 і Х2 = +00112
10 Виконати ділення двійкових нормалізованих чисел А = 0,1001 • 21 і В= 0,100 • 211 .
11 Виконати додавання в АЛП двох десяткових чисел А= 7 і В = 6.
12 Записати десяткове число 61 в двійково – десятковій системі числення.
13 Представити десяткове число А = 0,00065 • 105 в нормалізованій формі.
14 Перетворити десяткове число 29 за схемою (10 с.ч.) → (2 с.ч.) → (8 с.ч.) → (10 с.ч.)
Варіант 3
1 Записати в нормалізованому вигляді наступне двійкове число: 11.1011101
2 Як буде представлено десяткове число 3,18 в двійковому вигляді в розрядній сітці в формі з плаваючою комою (32 розряди, з них 7 розрядів – порядок числа) ?

3 Записати, як буде представлено в АЛП десяткове число -48 в прямому, зворотному, додатковому кодах
4 Знайдіть десятковий еквівалент числа представленого в додатковому коді: 0.100011
5 Виконати множення над цілими числами Х1 = +11002 і Х2 = -10102, представлених у формі з фіксованою точкою.
6 Додати двійкові нормалізовані числа А = 0,10101 • 2-1 і В= 0,101 • 211.
7 Виконати віднімання двійкових нормалізованих чисел А = 0,10101 • 210 і В= 0,101 • 201.
8 Виконати множення двійкових нормалізованих чисел А= 0,1011 • 211 і В= 0,111 • 2101.
9 Додати двійкові числа у модифікованому додатковому коді Х1 = +11002 і Х2 = -10102,
10 Виконати ділення двійкових нормалізованих чисел А = 0,10101 • 2100 і В= 0,101 • 211.
11 Виконати додавання в АЛП двох десяткових чисел А= 5 і В = 8.
12 Записати десяткове число 41 в двійково – десятковій системі числення.
13 Представити десяткове число А = 0,00178 • 107 в нормалізованій формі.
14 Перетворити десяткове число 49 за схемою (10 с.ч.) → (2 с.ч.) → (8 с.ч.) → (10 с.ч.)
Варіант 4
1 Записати в нормалізованому вигляді наступне двійкове число: 1.10111001
2 Як буде представлено десяткове число 7,35 в двійковому вигляді в розрядній сітці в формі з плаваючою комою (32 розряди, з них 7 розрядів – порядок числа) ?

3 Записати, як буде представлено в АЛП десяткове число -54 в прямому, зворотному, додатковому кодах
4 Знайдіть десятковий еквівалент числа представленого в додатковому коді: 0.101010
5 Виконати множення над цілими числами А = -110002 і В = +10012, представлених у формі з фіксованою точкою.
6 Додати двійкові нормалізовані числа А = 0,10101 • 2-1 і В= 0,101 • 210.
7 Виконати віднімання двійкових нормалізованих чисел А = 0,10101 • 2100 і В= 0,101 • 211.
8 Виконати множення двійкових нормалізованих чисел А = 0,10101 • 210 і В= 0,101 • 211.
9 Додати двійкові числа у модифікованому додатковому коді А = -110002 і В = +10012
10 Виконати ділення двійкових нормалізованих чисел А = 0,10101 • 2110 і В= 0,101 • 211.
11 Виконати додавання в АЛП двох десяткових чисел А = 7 і В = 4.
12 Записати десяткове число 21 в двійково – десятковій системі числення.
13 Представити десяткове число А = 0,000078 • 103 в нормалізованій формі.
14 Перетворити десяткове число 35 за схемою (10 с.ч.) → (2 с.ч.) → (8 с.ч.) → (10 с.ч.)
Варіант 5
1 Записати в нормалізованому вигляді наступне двійкове число: 101.1011101
2 Як буде представлено десяткове число 6,26 в двійковому вигляді в розрядній сітці в формі з плаваючою комою (32 розряди, з них 7 розрядів – порядок числа) ?

3 Записати, як буде представлено в АЛП десяткове число -61 в прямому, зворотному, додатковому кодах
4 Знайдіть десятковий еквівалент числа представленого в додатковому коді: 0.1011
5 Виконати множення над цілими числами Х1 = -10012 і Х2 = +0112, представлених у формі з фіксованою точкою
6 Додати двійкові нормалізовані числа А = 0,11101 • 210 і В= 0,10111 • 211.
7 Виконати віднімання двійкових нормалізованих чисел А = 0,11101 • 211 і В= 0,10111 • 210.
8 Виконати множення двійкових нормалізованих чисел А= 0,1101 • 2101 і В= 0,1010 • 211.
9 Додати двійкові числа у модифікованому додатковому коді А = -10012 і В = +0112
10 Виконати ділення двійкових нормалізованих чисел А = 0,11101 • 2110 і В= 0,111 • 2101.
11 Виконати додавання в АЛП двох десяткових чисел А = 7 і В = 3.
12 Записати десяткове число 57 в двійково – десятковій системі числення.
13 Представити десяткове число А = 0,0027 • 105 в нормалізованій формі.
14 Перетворити десяткове число 32 за схемою (10 с.ч.) → (2 с.ч.) → (8 с.ч.) → (10 с.ч.)
ЗАКРІПЛЕННЯ ВИВЧЕНОГО І ОЦІНЮВАННЯ РІВНЯ ЗНАНЬ: перевірка і оцінювання за рівнем повноти і правильності визначення області роботи транзистора, аналізу роботи статичного й динамічного режимів роботи ключів на біполярних транзисторах
ДОМАШНЄ ЗАВДАННЯ: самостійно вирішити наступні завдання:
1 Записати в нормалізованому вигляді наступне двійкове число: 100111.101.
2 Як буде представлено десяткове число 38,15 в розрядній сітці в формі з плавоючою комою в форматі слова (32 розряди, з них 7 розрядів – порядок, 32 розряди – мантиса).
3 Записати, як буде представлено в АЛП десяткове число -31 в прямому, зворотному, додатковому кодах.
4 Знайдіть десятковий еквівалент числа представленого в додатковому коді: 0.10111.
5 Виконати арифметичні операції над цілими числами Х1 = -11002 і Х2 = +01112, представлених у формі з фіксованою точкою
а) множення
б) ділення.
6 Як буде представлено десяткове число 9,26 в двійковому вигляді в розрядній сітці в формі з плаваючою комою (32 розряди, з них 7 розрядів – порядок числа)?

7 Записати, як буде представлено в АЛП десяткове число -34 в прямому, зворотному, додатковому кодах
8 Знайдіть десятковий еквівалент числа представленого в додатковому коді: 0.10011.
9 Виконати множення над цілими числами Х1 = -1112 і Х2 = +10012, представлених у формі з фіксованою точкою.
ВИКЛАДАЧ –Т.І.Ковальова
МЕТА:
- навчальна: вчити виконувати спрощення логічних виразів, використовуючи тотожності і аксіоми алгебри логіки;
- розвиваюча: розвивати вміння працювати за зразком і вказівками викладача, самостійно застосовувати знання до вирішення практичних завдань;
- виховна: виховати увагу, логічне мислення, впевненість у вирішенні практичних завдань:
ОБЛАДНАННЯ: ручка
ПЛАН
1 Логічні операції та функції.
2 Закони алгебри логіки
ЗМІСТ ПРАКТИЧНОГО ЗАНЯТТЯ
За індивідуальним варіантом завдання треба:
- уважно ознайомиться з завданням;
- виконати спрощення логічних виразів, використовуючи тотожності і аксіоми;
- довести тотожності алгебри логіки;
- використовуючи таблиці істинності, довести тотожності алгебри логіки;
- записати функції, задані таблицями істинності, в ДДНФ або в ДКНФ.
Варіанти завдань:
Варіант 1
1 Виконати спрощення логічних виразів, використовуючи тотожності і аксіоми
 а) у = х1 ∙ х2 + х1 ∙ х2
а) у = х1 ∙ х2 + х1 ∙ х2
2 Доведіть тотожності алгебри логіки
а) х1 ∙ (х1 + х2) = х1
3 Використовуючи таблиці істинності, доведіть тотожності алгебри логіки


 а) х1 + х2 = х1 ∙ х2
а) х1 + х2 = х1 ∙ х2
4 Запишіть функції, задані таблицями істинності, в ДДНФ:
| х1 | х2 | у |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
5 Використовуючи закони алгебри логіки, спростите логічний вираз

 у1 = х1 ∙ х2 + х1 ∙ х2 + х1 ∙ х2
у1 = х1 ∙ х2 + х1 ∙ х2 + х1 ∙ х2
Варіант 2
1 Виконати спрощення логічних виразів, використовуючи тотожності і аксіоми


 а) у = х1 ∙ х2 + х1 ∙ х2.
а) у = х1 ∙ х2 + х1 ∙ х2.
2 Доведіть тотожності алгебри логіки
 а) (х1 + х2)∙(х1 + х2) = х1.
а) (х1 + х2)∙(х1 + х2) = х1.
3 Використовуючи таблиці істинності, доведіть тотожності алгебри логіки:


 а) х1 ∙ х2 = х1 + х2
а) х1 ∙ х2 = х1 + х2
4 Запишіть функції, задані таблицями істинності, в ДКНФ:
| х1 | х2 | у |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
5 Використовуючи закони алгебри логіки, спростите логічний вираз:


 у1 = х1 ∙ х2 + х1 ∙ х2 + х1 ∙ х2
у1 = х1 ∙ х2 + х1 ∙ х2 + х1 ∙ х2
Варіант 3
1 Виконати спрощення логічних виразів, використовуючи тотожності і аксіоми
а) у = х1 + х1 ∙ х2 + х3.
2 Доведіть тотожності алгебри логіки
а) х1 + х2 ∙х3 = (х1 + х2) ∙ (х1 + х3)
3 Використовуючи таблиці істинності, доведіть тотожності алгебри логіки


 а) х1 + х2 = х1 ∙ х2.
а) х1 + х2 = х1 ∙ х2.
4 Запишіть функції, задані таблицями істинності, в ДДНФ:
| х1 | х2 | у |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
5 Використовуючи закони алгебри логіки, спростите логічний вираз

 у1 = (х1 + х2) ∙ (х1 + х2) ∙ (х1 + х2)
у1 = (х1 + х2) ∙ (х1 + х2) ∙ (х1 + х2)
Варіант 4
1 Виконати спрощення логічних виразів, використовуючи тотожності і аксіоми

 а) у = х1 ∙ (х1 + х2) + х2∙(х2 + х3) + х3
а) у = х1 ∙ (х1 + х2) + х2∙(х2 + х3) + х3
2 Доведіть тотожності алгебри логіки
а) х1 ∙ (х1 + х2) = х1
3 Використовуючи таблиці істинності, доведіть тотожності алгебри логіки


 а) х1 ∙ х2 = х1 + х2
а) х1 ∙ х2 = х1 + х2
4 Запишіть функції, задані таблицями істинності, в ДКНФ
| х1 | х2 | у |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
5 Використовуючи закони алгебри логіки, спростите логічний вираз:


 у = х1 ∙ х2 ∙ х3 + х1 ∙ х2 ∙ х3
у = х1 ∙ х2 ∙ х3 + х1 ∙ х2 ∙ х3
Варіант 5
1 Виконати спрощення логічних виразів, використовуючи тотожності і аксіоми
 а) у = х1 ∙ х2 + х1 ∙ х2
а) у = х1 ∙ х2 + х1 ∙ х2
2 Доведіть тотожності алгебри логіки
а) х1 ∙ (х1+х2) = х1.
3 Використовуючи таблиці істинності, доведіть тотожності алгебри логіки
 |

 а) х1 ∙ х2 = х1 + х2.
а) х1 ∙ х2 = х1 + х2.
МЕТА:
- навчальна: вчити мінімізувати логічні рівняння за допомогою класичного методу та діаграм Вейча-Карно;
- розвиваюча: розвивати вміння працювати за зразком і вказівками викладача, самостійно застосовувати знання до вирішення практичних завдань;
- виховна: виховати увагу, логічне мислення, впевненість у вирішенні практичних завдань:
ОБЛАДНАННЯ: ручка
ПЛАН
1 Мінімізація логічних рівнянь.
2 Класичний метод мінімізації.
3 Метод мінімізації Вейча-Карно
ЗМІСТ ПРАКТИЧНОГО ЗАНЯТТЯ
За індивідуальним варіантом завдання треба:
- уважно ознайомиться з завданням;
- де потрібно, зробити розрахунки;
- виберіть правильну відповідь до тестового завдання із останньої колонки.
Варіанти завдань:
Варіант 1
1 За заданою таблицею істинності записати досконалі ДДНФ і ДКНФ.
| Номера комбінацій | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| х1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| х2 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| х3 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| f(x1,x2,x3) | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 |
2 За отриманою функцією ДДНФ і ДКНФ скласти карту Вейча.
3 Мінімізувати логічну функцію за картою Вейча.
4 Побудувати функціональну схему на логічних елементах І, АБО, НЕ, що реалізує отриману мінімізовану функцію.
5 Побудувати за логічною функцією МДНФ комбінаційний пристрій на однотипних елементах 2АБО-НЕ і 2І-НЕ.
Варіант 2
1 За заданою таблицею істинності записати досконалі ДДНФ і ДКНФ.
| Номера комбінацій | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| х1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| х2 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| х3 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| f(x1,x2,x3) | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 |
2 За отриманою функцією ДДНФ і ДКНФ скласти карту Вейча.
3 Мінімізувати логічну функцію за картою Вейча.
4 Побудувати функціональну схему на логічних елементах І, АБО, НЕ, що реалізує отриману мінімізовану функцію.
5 Побудувати за логічною функцією МДНФ комбінаційний пристрій на однотипних елементах 2АБО-НЕ і 2І-НЕ.
Варіант 3
1 За заданою таблицею істинності записати досконалі ДДНФ і ДКНФ.
| Номера комбінацій | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| х1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| х2 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| х3 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| f(x1,x2,x3) | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
2 За отриманою функцією ДДНФ і ДКНФ скласти карту Вейча.
3 Мінімізувати логічну функцію за картою Вейча.
4 Побудувати функціональну схему на логічних елементах І, АБО, НЕ, що реалізує отриману мінімізовану функцію.
5 Побудувати за логічною функцією МДНФ комбінаційний пристрій на однотипних елементах 2АБО-НЕ і 2І-НЕ.
Варіант 4
1 За заданою таблицею істинності записати досконалі ДДНФ і ДКНФ.
| Номера комбінацій | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| х1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| х2 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| х3 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| f(x1,x2,x3) | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 |
2 За отриманою функцією ДДНФ і ДКНФ скласти карту Вейча.
3 Мінімізувати логічну функцію за картою Вейча.
4 Побудувати функціональну схему на логічних елементах І, АБО, НЕ, що реалізує отриману мінімізовану функцію.
5 Побудувати за логічною функцією МДНФ комбінаційний пристрій на однотипних елементах 2АБО-НЕ і 2І-НЕ.
Варіант 5
1 За заданою таблицею істинності записати досконалі ДДНФ і ДКНФ.
| Номера комбінацій | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| х1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| х2 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| х3 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| f(x1,x2,x3) | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 |
2 За отриманою функцією ДДНФ і ДКНФ скласти карту Вейча.
3 Мінімізувати логічну функцію за картою Вейча.
4 Побудувати функціональну схему на логічних елементах І, АБО, НЕ, що реалізує отриману мінімізовану функцію.
5 Побудувати за логічною функцією МДНФ комбінаційний пристрій на однотипних елементах 2АБО-НЕ і 2І-НЕ.
МЕТА:
- навчальна: вчити синтезувати пристрої у заданому базисі та аналізувати роботу логічних комбінаційних пристроїв;
- розвиваюча: розвивати вміння працювати за зразком і вказівками викладача, самостійно застосовувати знання до вирішення практичних завдань;
- виховна: виховати увагу, логічне мислення, впевненість у вирішенні практичних завдань:
ОБЛАДНАННЯ: ручка, олівець
ПЛАН
1 Синтез логічних пристроїв у заданому базисі.
2 Логічні елементи для реалізації складних функцій.
3 Особливості побудови логічних пристроїв на реальній елементній базі.
ЗМІСТ ПРАКТИЧНОГО ЗАНЯТТЯ
За індивідуальним варіантом завдання треба:
- уважно ознайомиться з завданням;
- синтезувати в базисі І-НЕ та дослідити комбінаційну схему, яка реалізує логічну функцію чотирьох змінних, задану таблицею істинності;
- синтезувати в базисі І-АБО-НЕ та дослідити комбінаційну схему, яка реалізує функцію трьох змінних, задану логічним виразом.
Варіанти завдань:
1 Синтезувати в базисі І-НЕ та дослідити комбінаційну схему, яка реалізує логічну функцію чотирьох змінних, задану наступною таблицею істинності:
| Х3 | X2 | Х1 | Х0 | |||||||
F (Х)
2 Синтезувати в базисі І-АБО-НЕ та дослідити комбінаційну схему, яка реалізує функцію трьох змінних, задану логічним виразом:
| Варіант | Вигляд логічної функції |
| 1 | 
|
| 2 | 
|
| 3 | 
|
| 4 | 
|
| 5 | 
|
| 6 | 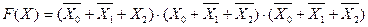
|
| 7 | 
|
| 8 | 
|
МЕТА:
- навчальна: вчити будувати комбінаційні схеми у заданому базисі та по заданій комбінаційній схемі записувати функцію, яку вона реалізує;
- розвиваюча: розвивати вміння працювати за зразком і вказівками викладача, самостійно застосовувати знання до вирішення практичних завдань;
- виховна: виховати увагу, логічне мислення, впевненість у вирішенні практичних завдань:
ОБЛАДНАННЯ: ручка, олівець
ПЛАН
1 Синтез логічних пристроїв у заданому базисі.
2 Логічні елементи для реалізації складних функцій.
3 Особливості побудови логічних пристроїв на реальній елементній базі.
ЗМІСТ ПРАКТИЧНОГО ЗАНЯТТЯ
За індивідуальним варіантом завдання треба:
- уважно ознайомиться з завданням;
- побудувати на двовходових логічних елементах функціональну схему пристрою, що реалізує функцію;
- записати логічну функцію, яку реалізує дана схема на рисунку;
- побудувати на логічних елементах 2І-НЕ, 2АБО-НЕ функціональну схему пристрою, що реалізує функцію
Варіанти завдань:
Варіант 1
 1 Побудувати на двовходових логічних елементах функціональну схему пристрою, що реалізує функцію
1 Побудувати на двовходових логічних елементах функціональну схему пристрою, що реалізує функцію  .
.
2 Записати логічну функцію, яку реалізує дана схема на рисунку
3 Побудувати на логічних елементах 2І-НЕ, 2АБО-НЕ функціональну схему пристрою, що реалізує функцію
 .
.
4 Визначити значення логічної функції на виході логічного елементу І-НЕ з двома входами, якщо на входи подано логічні змінні х1=1, х2=1
А) 10 Б) 00 В) 0 Г) 00 Д) 1 Е) 01
Варіант 2
1 Побудувати на двовходових логічних елементах функціональну схему пристрою, що реалізує функцію

2 Записати логічну функцію, яку реалізує дана схема на рисунку
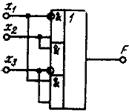
3 Побудувати на логічних елементах 2І-НЕ, 2АБО-НЕ функціональну схему пристрою, що реалізує функцію

4 Визначити значення логічної функції на виході логічного елементу І-НЕ з двома входами, якщо на входи подано логічні змінні х1=1, х2=1
А) 0 Б) 01 В) 10 Г) 1 Д) 11 Е) 00
Варіант 3
1 Побудувати на двовходових логічних елементах функціональну схему пристрою, що реалізує функцію

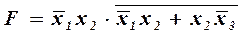
2 Записати логічну функцію, яку реалізує дана схема на рисунку
3 Побудувати на логічних елементах 2І-НЕ, 2АБО-НЕ функціональну схему пристрою, що реалізує функцію

4 Визначити значення логічної функції на виході логічного елементу І-НЕ з двома входами, якщо на входи подано логічні змінні х1=1, х2=1
А) 0 Б) 01 В) 10 Г) 1 Д) 11 Е) 00
Варіант 4
1 Побудувати на двовходових логічних елементах функціональну схему пристрою, що реалізує функцію
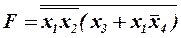
2 Записати логічну функцію, яку реалізує дана схема на рисунку

3 Побудувати на логічних елементах 2І-НЕ, 2АБО-НЕ функціональну схему пристрою, що реалізує функцію

4 Визначити значення логічної функції на виході логічного елементу І-НЕ з двома входами, якщо на входи подано логічні змінні х1=1, х2=1
А) 0 Б) 01 В) 10 Г) 1 Д) 11 Е) 00
Варіант 5
1 Побудувати на двовходових логічних елементах функціональну схему пристрою, що реалізує функцію

2 Записати логічну функцію, яку реалізує дана схема на рисунку

3 Побудувати на логічних елементах 2І-НЕ, 2АБО-НЕ функціональну схему пристрою, що реалізує функцію

4 Визначити значення логічної функції на виході логічного елементу АБО-НЕ з двома входами, якщо на входи подано логічні змінні х1=1, х2=1
А) 0 Б) 01 В) 10 Г) 1 Д) 11 Е) 00
Варіант 6
1 Побудувати на двовходових логічних елементах функціональну схему пристрою, що реалізує функцію


2 Записати логічну функцію, яку реалізує дана схема на рисунку
3 Побудувати на логічних елементах 2І-НЕ, 2АБО-НЕ функціональну схему пристрою, що реалізує функцію

4 Визначити значення логічної функції на виході логічного елементу АБО-НЕ з двома входами, якщо на входи подано логічні змінні х1=1, х2=1
А) 0 Б) 01 В) 10 Г) 1 Д) 11 Е) 00
ЧЕРНІГІВСЬКИЙ НАЦІОНАЛЬНИЙ ТЕХНОЛОГІЧНИЙ УНІВЕРСИТЕТ
Последнее изменение этой страницы: 2019-04-10; Просмотров: 339; Нарушение авторского права страницы