
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Некоторые формулы векторной алгебры ⇐ ПредыдущаяСтр 7 из 7
Линейные операции. v В декартовых координатах линейные операции над парой векторов выполняются по формулам v Линейные операции над произвольным числом векторов сводятся к линейным операциям над парами. Скалярное произведение. v В декартовых координатах скалярное произведение вычисляется по формуле v Скалярное произведение любого вектора на себя дает квадрат его длины v Скалярное произведение ортогональных (взаимно перпендикулярных) векторов равно нулю. Векторное произведение. v В декартовых координатах векторное произведение вычисляется по формуле v Векторное произведение перпендикулярно каждому из своих сомножителей. v Длина векторного произведения равна площади параллелограмма (удвоенной площади треугольника), построенного на сомножителях, и вычисляется через длины сомножителей и угол между ними по формуле Смешанное произведение. v В декартовых координатах смешанное произведение вычисляется по формуле v Модуль смешанного произведения равен объему параллелепипеда (шести объемам тетраэдра), построенного на сомножителях. Смешанное произведение компланарных векторов равно нулю.
ГЛОССАРИЙ | |||||
| № п/п |
Новые понятия | Содержание | |||
| 1 |
Линейное пространство | множество V элементов произвольной природы, в котором определены операции сложения 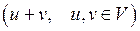 и умножения на число и умножения на число  , подчиняющиеся определенным аксиомам , подчиняющиеся определенным аксиомам
| |||
| 2 | Коммутативность сложения векторов | свойство операции сложения | |||
| 3 | Ассоциативность сложения векторов | свойство операции сложения: | |||
| 4 | Пространство непрерывных функций на отрезке 
| совокупность функций, непрерывных на отрезке  , с обычными операциями сложения функций и умножения функции на число; обозначается , с обычными операциями сложения функций и умножения функции на число; обозначается 
| |||
| 5 | Арифметическое пространство Rn | совокупность упорядоченных наборов  действительных чисел, где определены операции сложения и умножения на число действительных чисел, где определены операции сложения и умножения на число
| |||
| 6 | Компоненты вектора 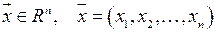
| числа | |||
| 7 | Вектор линейного пространства | элемент линейного пространства V | |||
| 8 | Линейная комбинация векторов  , принадлежащих пространству V , принадлежащих пространству V
| вектор | |||
| 9 | Линейно независимая система векторов | Совокупность векторов  , для которых равенство , для которых равенство  выполняется тогда и только тогда, когда числа выполняется тогда и только тогда, когда числа  . .
| |||
| 10 | Базис линейного пространства V | конечная система линейно независимых векторов, через которые линейно выражается любой вектор пространства | |||
| 11 | Линейная оболочка  системы векторов системы векторов 
| совокупность всевозможных линейных комбинаций этих векторов | |||
| 12 | Разложение вектора и по базису 
| это однозначное представление | |||
| 13 | Координаты вектора и в базисе  . .
| коэффициенты в разложении вектора по базису | |||
| 14 | Размерность dim V подпространства V | число векторов базиса | |||
| 15 | Скалярное произведение двух векторов (u,v) | скалярная функция двух векторных аргументов, подчиняющаяся определенным законам:

| |||
| 16 | Евклидово пространство Е | линейное пространство, в котором введено скалярное произведение | |||
| 17 |
Ортогональные векторы | векторы | |||
| 18 | Ортонормированный базис 
| базис пространства Е, для которого выполнено свойство 
| |||
| 19 | Неравенство Коши-Буняковского | неравенство | |||
| 20 |
Процесс ортогонализации | способ построения ортонормированного базиса по произвольному | |||
| 21 | Матрица | матрица, элементы которой  - любые векторы пространства Е - любые векторы пространства Е
| |||
| 22 | Линейный оператор А в линейном пространстве V | правило, по которому каждому вектору  ставится в соответствие некоторый вектор ставится в соответствие некоторый вектор  , причем , причем 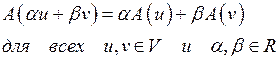
| |||
| 23 | Матрица А линейного оператора А в базисе 
| квадратная матрица 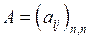 элементы которой элементы которой  определяются из соотношений определяются из соотношений 
| |||
| 24 | Матрица перехода от базиса  ,к базису ,к базису 
| матрица  , элементами которой , элементами которой 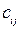 являются координаты вектора являются координаты вектора 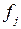 по базису по базису 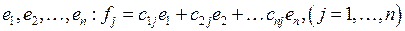
| |||
| 25 | Оператор  , сопряженный к оператору , сопряженный к оператору 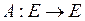
| оператор, действующий в пространстве  такой, что такой, что  для любых для любых 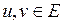
| |||
| 26 | Самосопряженный оператор А | такой оператор, который совпадает со своим сопряженным | |||
| 27 |
Симметричная матрица | матрица А, для которой At = A | |||
| 28 | Ортогональная матрица 
| матрица, элементы которой удовлетворяют равенству: 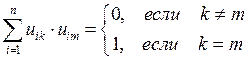
| |||
| 29 | Собственный вектор v оператора А | ненулевой вектор  , удовлетворяющий соотношению , удовлетворяющий соотношению 
| |||
| 30 | Собственное значение (собственное число), соответствующее собственному вектору v оператора А | число | |||
| 31 | Характеристический многочлен матрицы А | многочлен n-й степени от | |||
| 32 | Характеристическое уравнение | уравнение | |||
| 33 | Корни характеристического уравнения | множество значений  , для которых , для которых  , являются собственными значениями оператора А , являются собственными значениями оператора А
| |||
| 34 | Собственное подпространство, отвечающее данному собственному значению | совокупность всех собственных векторов оператора А, отвечающих данному собственному значению | |||
| 35 | Собственный базис самосопряженного оператора | базис из собственных векторов симметрической матрицы этого оператора | |||
| 36 | Линейная форма на линейном пространстве V | функция  , удовлетворяющая соотношению , удовлетворяющая соотношению 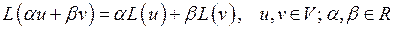 . Линейная форма может быть записана в виде: . Линейная форма может быть записана в виде:  , где , где  - данный вектор - данный вектор
| |||
| 37 | Билинейная форма на линейном пространстве V | функция  двух векторных аргументов двух векторных аргументов  , линейная по каждому аргументу , линейная по каждому аргументу
| |||
| 38 |
Квадратичная форма | функция вида | |||
| 39 | Матрица билинейной формы  в базисе в базисе 
| матрица | |||
| 40 | Матрица квадратичной формы | матрица соответствующей симметричной билинейной формы | |||
| 41 | Координатная запись квадратичной формы Q(v) | запись квадратичной формы в виде 
| |||
| 42 | Канонический вид квадратичной формы Q(v) | координатная запись формы, не содержащая произведений  , т.е. содержащая лишь квадраты координат , т.е. содержащая лишь квадраты координат
| |||
| 43 | Положительно определенная квадратичная форма Q(v) | форма | |||
| 44 | Неотрицательно определенная квадратичная форма | форма | |||
| 45 |
Критерий Сильвестра | теорема о необходимом и достаточном условии положительной определенности квадратичной формы | |||
| 46 |
Закон инерции | теорема о сохранении числа положительных, отрицательных и нулевых коэффициентов в каноническом виде, не зависимо от способа приведения квадратичной формы к сумме квадратов | |||
| 47 |
Метод итерации | численный метод последовательного приближения к решению | |||
| 48 |
Гессиан | определитель n-го порядка, элементами которого являются вторые частные производные функции n переменных | |||
ПЕРЕЧЕНЬ УМЕНИЙ
| № п/п | Умение | Алгоритмы |
| 1 | Проведение доказательства принадлежности множества с определенными в нем операциями к линейным пространствам | 1. Выбрав два элемента a и b заданного множества, проверить выполнение закона коммутативности сложения a+ b= b+ a.
2. Выбрав три элемента a, b, c множества, проверить выполнение закона ассоциативности сложения ( a+ b)+ c= a+( b+ c).
3. Найти во множестве нулевой элемент, т.е. элемент 0 такой, что 0+ a= a.
4. Выбрав элемент a множества, найти противоположный ему элемент, т.е элемент(- a) такой, что a+(- a)=0.
5. Проверить для числа 1 выполнение равенства 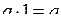 .
6. Для чисел .
6. Для чисел  проверить выполнение равенства проверить выполнение равенства  ;
7. Проверить для чисел ;
7. Проверить для чисел  выполнение равенства выполнение равенства  .
8. Для двух элементов множества .
8. Для двух элементов множества 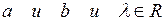 проверить выполнение равенства проверить выполнение равенства  . .
|
| 2 | Исследование системы векторов на линейную независимость | 1. Составить линейную комбинацию из заданных векторов с неизвестными коэффициентами 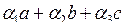 .
2. Приравнять линейную комбинацию векторов нулевому вектору.
3. Записать покоординатные равенства в систему.
4. Решить систему уравнений относительно неизвестных коэффициентов, для чего привести матрицу системы к ступенчатому виду.
5. Определить число ненулевых угловых элементов в ступенчатой матрице – оно определяет число линейно независимых векторов в рассматриваемой системе векторов. .
2. Приравнять линейную комбинацию векторов нулевому вектору.
3. Записать покоординатные равенства в систему.
4. Решить систему уравнений относительно неизвестных коэффициентов, для чего привести матрицу системы к ступенчатому виду.
5. Определить число ненулевых угловых элементов в ступенчатой матрице – оно определяет число линейно независимых векторов в рассматриваемой системе векторов.
|
| 3 | Определение размерности линейного пространства | 1. Записать матрицу А для однородной системы алгебраических уравнений. 2. Решить систему алгебраических уравнений. 3. По общему решению системы найти фундаментальную систему решений, взяв в качестве значений свободных переменных такие, чтобы матрица, составленная из них, была единичной матрицей порядка, равного числу свободных переменных. 4. Определить размерность линейного пространства решений системы, которое равно количеству векторов, образующих фундаментальную систему решений. |
| 4 | Определение координат вектора в произвольном базисе | 1. Составить матрицу перехода U от базиса b к базису e, поставив в первый столбец матрицы коэффициенты первого уравнения, во второй столбец коэффициенты второго уравнения и т.д.
2. Найти матрицу  , обратную матрице , обратную матрице  .
3. Найти координаты вектора x в базисе e, для чего вычислить произведение .
3. Найти координаты вектора x в базисе e, для чего вычислить произведение  , где x – столбец координат вектора x в базисе b, а x’ - столбец координат вектора x в базисе e.
4. Записать вектор x в базисе , где x – столбец координат вектора x в базисе b, а x’ - столбец координат вектора x в базисе e.
4. Записать вектор x в базисе 
|
| 5 | Преобразование матрицы линейного оператора при переходе к другому базису | 1. Составить матрицу перехода U от базиса e к базису b, поставив в первый столбец матрицы коэффициенты первого уравнения, во второй столбец коэффициенты второго уравнения и т.д.
2. Найти матрицу  , обратную матрице , обратную матрице  .
3. Найти произведение матриц .
3. Найти произведение матриц  .
4. Найти произведение матриц .
4. Найти произведение матриц  равное матрице оператора A в базисе b. равное матрице оператора A в базисе b.
|
| 6 | Вычисление собственных значений и собственных векторов матрицы | 1. Составить характеристический многочлен  для матрицы для матрицы  линейного оператора А.
2. Получить характеристическое уравнение оператора А, для чего приравнять характеристический многочлен нулю.
3. Найти корни характеристического уравнения, разрешив его относительно неизвестного линейного оператора А.
2. Получить характеристическое уравнение оператора А, для чего приравнять характеристический многочлен нулю.
3. Найти корни характеристического уравнения, разрешив его относительно неизвестного  , полученные корни – собственные значения линейного оператора.
4. Составить систему уравнений для определения собственных векторов, соответствующих собственному значению , полученные корни – собственные значения линейного оператора.
4. Составить систему уравнений для определения собственных векторов, соответствующих собственному значению  .
5. Найти фундаментальную систему решений полученной системы линейных алгебраических уравнений.
6. Составить систему уравнений для определения собственных векторов, соответствующих собственному значению .
5. Найти фундаментальную систему решений полученной системы линейных алгебраических уравнений.
6. Составить систему уравнений для определения собственных векторов, соответствующих собственному значению  7. Найти фундаментальную систему решений полученной системы линейных алгебраических уравнений.
8. Составить систему уравнений для определения собственных векторов, соответствующих собственному значению
7. Найти фундаментальную систему решений полученной системы линейных алгебраических уравнений.
8. Составить систему уравнений для определения собственных векторов, соответствующих собственному значению  9. Найти фундаментальную систему решений полученной системы линейных алгебраических уравнений.
9. Найти фундаментальную систему решений полученной системы линейных алгебраических уравнений.
|
| 7 | Построение ортогонального базиса по заданному | 1. Составить матрицу А из координат векторов  , записав в первый столбец матрицы координаты вектора , записав в первый столбец матрицы координаты вектора  , во второй – координаты вектора , во второй – координаты вектора  , а в третий координаты вектора , а в третий координаты вектора  .
2. Вычислить определитель матрицы .
2. Вычислить определитель матрицы  .
3. Если матрица А удовлетворяет условию .
3. Если матрица А удовлетворяет условию  , то заданная система векторов образует базис в , то заданная система векторов образует базис в  и может быть взята за исходную для построения ортонормированного базиса. В противном случае заданную систему векторов использовать для построения ортонормированного базиса нельзя.
4. Вычислить векторы и может быть взята за исходную для построения ортонормированного базиса. В противном случае заданную систему векторов использовать для построения ортонормированного базиса нельзя.
4. Вычислить векторы  5. Вычислить векторы
5. Вычислить векторы 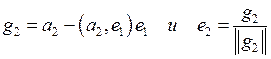 6. Вычислить векторы
6. Вычислить векторы 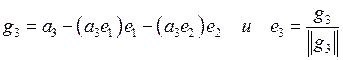
|
| 8 | Приведение квадратичной формы к каноническому виду методом выделения квадратов | 1. Сгруппировать члены квадратичной формы, содержащей квадрат переменной х и её произведение на какую-либо другую переменную, квадрат переменной у и её произведение на переменную, отличную от х. 2. Дополнить каждое из выражений, стоящих в скобках, до полного квадрата, вычитая из всего уравнения дополнительно прибавленные члены, чтобы оно не изменилось по сравнению с исходным видом квадратичной формы. 3. Записать квадратичную форму в виде суммы квадратов, получившихся в результате преобразований. 4. Перейти к новым координатам; заменив каждое из выражений, возводимое в квадрат, на новую координату, получить канонический вид записи квадратичной формы. |
| 9 | Приведение квадратичной формы к каноническому виду ортогональным преобразованием | 1. Составит матрицу квадратичной формы. 2. Составить характеристическое уравнение для матрицы А и найти его корни (собственное значение квадратичной формы). 3. Найти канонический вид квадратичной формы. 4. Найти собственные векторы, соответствующие собственным значениям. 5. Пронормировать собственные векторы. 6. Составить из столбцов координат прнормированных собственных векторов матрицу ортонормированного преобразования, приводящего квадратичную форму к каноническому виду. |
Литература
1. Александров П.С. Курс аналитической геометрии и линейной алгебры. – М.: Наука, 1979.
2. Беклемешев Д.В. Линейная алгебра. – М.: Наука, 1980.
3. Воеводин В.В. Курс аналитической геометрии и линейной алгебры. – М.: Наука, 1984.
4. Гельфанд И.М. Лекции по линейной алгебре. – М., 1971.
5. Икрамов Х.Д. Задачник по линейной алгебре. – М., 1975.
6. Ильин В.А., Поздняк Э.Г. Линейная алгебра. – М., 1974.
7. Курош А.Г. Курс высшей алгебры. М: Физматгиз, 1962.
8. Мальцев А.И. Основы линейной алгебра. М.: Наука, 1970.
9. Проскуряков И.В. Сборник задач по линейной алгебре. М.: Наука, 1978.
10. Тышкевич В.И., Феденко А.С. Линейная алгебра и аналитическая геометрия. Минск: Вышэйша школа, 1968.
11. Фаддеев Д.К. Лекции по линейной алгебре. М.: Наука, 1984.
Последнее изменение этой страницы: 2019-04-10; Просмотров: 371; Нарушение авторского права страницы