Расчет на контактную прочность

Вследствие наклона зубьев в зацеплении одновременно находится несколько пар зубьев, что уменьшает нагрузку на один зуб, повышая его прочность (снижая расчётные напряжения).

Аналогично расчету прямозубой передачи межосевое расстояние для косозубых колес определяют по формуле (2.3.17):

,

 

где Ка = 43 МПа – для косозубых колес.

Контактные напряжения в поверхностном слое зубьев

,

 

где - коэффициент нагрузки при расчете по контактным напряжениям;
- 1,04 – 1,13 коэффициент нагрузки, учитывающий распределение нагрузки между зубьями и зависит от окружной скорости;
- коэффициент нагрузки, учитывающий неравномерность распределения нагрузки по ширине зубчатого венца (по длине контактных линий); для косозубых передач выбирается с учетом расположения колеса на валу и термообработки;
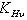- коэффициент нагрузки, учитывающий дополнительные динамические нагрузки
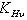=1,02-1,06 при любой твердости, скорость до 10 м/с,
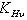=1,1 при твердости поверхности не больше 350 НВ и скорости 10-20 м/с,
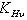=1,05 при твердости более 350 НВ и скорости 10-20 м/с.

Косозубые передачи работают более плавно, чем прямозубые, поэтому коэффициент 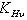, меньше.

Условие контактной прочности косозубой передачи

,

 

Если условие не выполняется, то изменяют ширину венца колеса b2, не выходя за пределы рекомендуемых значений 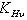. Если это не даст желательного результата, то либо назначает другие материалы колёс или другую термообработку, и расчёт повторяют.

Расчет допускаемых напряжений ведется аналогично расчету прямозубых колес

Расчёт зубьев на изгиб

Наклонное расположение зубьев увеличивает их прочность на изгиб и уменьшает динамические нагрузки. Это учитывается введением в расчётную формулу прямозубых передач поправочных коэффициентов и 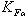. Формула проверочного расчёта косозубых передач

(2.3.41),

 

где YF - коэффициент формы зуба выбирают по эквивалентному числу зубьев zv; 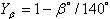- коэффициент, учитывающий наклон зуба; 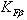- коэффициент распределения нагрузки по ширине венца определяют по аналогии с прямозубыми передачами; 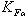= 0,81-0,91 - коэффициент распределения нагрузки между зубьями; - коэффициент нагрузки, учитывающий дополнительные динамические нагрузки =1,2 при твердости зубьев не больше 350НВ, = 1,1 при твердости зубьев более 350 НВ. Нормальный модуль зубьев mn определяют по аналогии с прямозубыми передачами. При некоторых средних значениях коэффициентов получим формулу для приближенного определения модуля косозубых передач

(2.3.42),

 

и для шевронных передач

(2.3.43),

 

При проверке по формуле (2.3.41): можно получить значительно меньше , что не является недопустимым, так как нагрузочная способность большинства передач ограничивается контактной прочностью, а не прочностью на изгиб.Если расчётное значение превышает допускаемое, то применяют колёса, нарезанные с положительным смещением инструмента, или увеличивают m; > означает, что в передаче из данных материалов решающее значение имеет не контактная прочность, а прочность зубьев на изгиб. На практике к таким передачам относятся передачи с высокой твёрдостью рабочих поверхностей зубьев – 51…63HRCэ (цементация, нитроцементация, азотирование). Проектировочный расчёт таких передач следует выполнять с целью обеспечения прочности зубьев на изгиб по форме определения минимально допустимого модуля m, а затем выполнить проверочный расчёт зубьев на контактную прочность.

24. Принципы и виды разрушения зубьев зубчатых передач; критерии их работоспособности и расчета.

⇐ Предыдущая45678910111213Следующая ⇒

Поделиться: