Структурная схема системы управления

Рисунок 2.1: Структурная схема системы управления.

Исходные данные

Передаточная функция объекта:

, где:

.

Передаточная функция фильтра:

.

2.4 Динамические требования к системе управления

Длительность переходного процесса:

Степень устойчивости системы:

.

Характеристическое уравнение замкнутой системы:

, где:

 — уравнение главных корней,

 — уравнение дополнительных корней,

.

Метод перехода от аналогового фильтра к цифровому

Полуаналитический с вычислением производных по входу:

интерполяционным методом:

и

экстраполяционным методом:

              

Проектирование аналоговой системы управления

Теоретическая часть

Найдём параметры аналогового фильтра.

Передаточная функция фильтра, выраженная через физические параметры:

.                                                                                                                         (3.1)

Передаточная функция объекта, выраженная через физические параметры:

.                                                                                                                          (3.2)

Найдём передаточную функцию разомкнутой системы как произведение передаточных функций объекта и фильтра:

.                                                                                                       (3.3)

Подставляя (3.1) и (3.2) в (3.3), получаем передаточную функцию разомкнутой системы, выраженную через физические параметры:

.                                                                                           (3.4)

Передаточная функция замкнутой системы определяется из передаточной функции разомкнутой системы как:

.                                                                                                               (3.5)

Подставляя (3.4) в (3.5), получаем передаточную функцию замкнутой системы, выраженную через физические параметры:

, откуда после упрощения:

.                                                     (3.6)

Знаменатель полученного выражения является характеристическим уравнением замкнутой системы, выраженным через физические параметры:

.                                                     (3.7)

С другой стороны, характеристическое уравнение замкнутой системы можно выразить через желаемые корни:

.                                                                                                              (3.8)

Здесь уравнение главных корней имеет вид:

.                                                                                                    (3.9)

А уравнение дополнительных корней имеет вид:

.                                                                                        (3.10)

Подставляя (3.9) и (3.10) в (3.8), получаем:

, откуда после упрощения:

.               (3.11)

Приравнивая коэффициенты при одинаковых степенях правых частей уравнений (3.7) и (3.11), получаем систему:

                                                                                                (3.12)

В этой системе 3 известных нам величины (в техническом задании заданы: , , ) и 5 неизвестных (физические параметры фильтра: , , , , ). Т.к. в системе 4 уравнения, найти мы можем лишь 4 из 5^и неизвестных величин, а оставшуюся, — пусть это будет параметр , — мы будем варьировать.

Решая систему (3.12), находим:

                                                                                                         (3.13)

Подставляя (3.13) в (3.1) и (3.6), получаем передаточные функции фильтра и замкнутой системы зависящими от параметра :

,                                                                          (3.14)

.                                                 (3.15)

Исследовательская часть

Путём варьирования параметра , найдём его оптимальное значение , при котором перерегулирование  в переходном процессе замкнутой системы минимально.

Переходный процесс, — по определению, — реакция системы на единичное ступенчатое входное воздействия. Для построения графика переходного процесса необходимо умножить передаточную функцию (3.15) замкнутой системы на величину  (подача единичного ступенчатого входного воздействия) и применить к полученному выражению обратное преобразование Лапласа. В результате мы получим значение выходного сигнала , — реакцию системы, — как функцию времени. Сделаем это:

, откуда после расчёта:

     (3.16)

Выражение (3.16) получено при условии отсутствия внешнего возмущения ( ).

Построим график переходного процесса замкнутой системы (график функции , описываемой выражением (3.16)) при 10 экспериментальных значениях : от 23 до 32 с шагом 1. В предположении, что к десятой секунде переходный процесс устоится, для каждого ( -того) полученного графика определим перерегулирование  как

, итак:

t

Рисунок 3.1: Переходный процесс замкнутой системы при .

, ,

 

t

Рисунок 3.2: Переходный процесс замкнутой системы при .

, ,

 

t

Рисунок 3.3: Переходный процесс замкнутой системы при .

, ,

t

Рисунок 3.4: Переходный процесс замкнутой системы при .

, ,

 

t

Рисунок 3.5: Переходный процесс замкнутой системы при .

, ,

 

t

Рисунок 3.6: Переходный процесс замкнутой системы при .

, ,

t

Рисунок 3.7: Переходный процесс замкнутой системы при .

, ,

 

t

Рисунок 3.8: Переходный процесс замкнутой системы при .

, ,

 

t

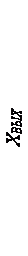
Рисунок 3.9: Переходный процесс замкнутой системы при .

, ,

t

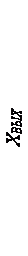
Рисунок 3.10: Переходный процесс замкнутой системы при .

, ,

При всех рассмотренных значениях  устоявшееся значение переходного процесса , т.к. входное воздействие является единичным ступенчатым, и, как видно из (3.16), .

Сведём полученные значения перерегулирования  в таблицу:

	23	24	25	26	27	28	29	30	31	32
	0.193	0.189	0.186	0.183	0.18176	0.18152	0.183	0.185	0.189	0.194

Таблица 3.1: Экспериментальная зависимость

Обозначив данные точки на плоскости , построим по ним аппроксимирующую функцию :

g2

Рисунок 3.11: Экспериментальная и аппроксимирующая её зависимости .

Минимизируя полученную функцию , находим оптимальное значение параметра  равным

                                                                                                                                                     (3.18)

Подставляя (3.18) в (3.14) и (3.15), получаем вид оптимальных передаточных функций фильтра и замкнутой системы:

;                                                                                               (3.19)

.                                                          (3.20)

⇐ Предыдущая1234Следующая ⇒

Поделиться: