Переходный процесс в замкнутой системе

В соответствии с выражением (3.16) с учётом (3.18),

t

Рисунок 3.13: Переходный процесс в замкнутой системе при различных значениях .

Время переходного процесса замкнутой системы, как момент его вхождения в пятипроцентный -коридор своего устоявшегося значения, составляет 0.334, 0.263 и 0.174 секунды для значений ,  и  соответственно. Все три значения удовлетворяет установленным в техническом задании требованиям (0.4 секунды). С ростом  время переходного процесса уменьшается.

Так же по полученным графикам видно, что с ростом значения 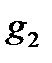 время наступления максимума переходного процесса уменьшается.

Кроме того, следует отметить, что вне зависимости от значения 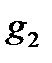 в определённые моменты времени выходной сигнал принимает строго определённые значения — графики имеют несколько (минимум две) общих точек, причём одна из них (первая по времени после нуля) приходится на максимум переходного процесса при . Это свойство позволяет нам найти значение  аналитически. Сделаем это. Рассмотрим уравнение:

, где функция  определяется выражением (3.16), а  и  — два произвольных значения . Перенося все члены уравнения в левую часть и приводя подобные, получаем:

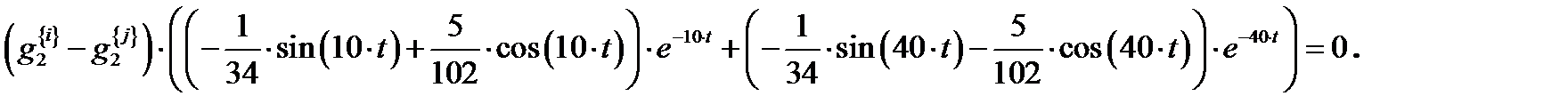Получено уравнение представляет собой равенство нулю произведения двух множителей. Т.о. либо первый, либо второй множитель равен нулю. Но мы рассматриваем общий случай , и равным нулю должен быть второй множитель:

.

Первым большим нуля решением полученного уравнения является значение

.                                                                                                                                                             (3.24)

Кривая из семейства  (при варьируемом значении ), имеющая локальный максимум при 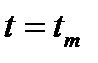, соответствует значению . Находя производную по времени функции :

, приравнивая её нулю при :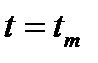

, и решая полученное уравнение, находим значение:

.                                                                                                                                                    (3.25)

Сравнивая теоретическое значение (3.25) 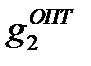 с полученным ранее экспериментальным значением (3.18), видим, что погрешность эксперимента составляет менее 0.004%.

Переходный процесс в фильтре

Для построения графика переходного процесса в фильтре необходимо умножить передаточную функцию (3.14) фильтра на величину 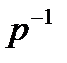 (подача единичного ступенчатого входного воздействия) и применить к полученному выражению обратное преобразование Лапласа:

, откуда после расчёта:

                                                (3.26)

Подставляя в (3.26) различные значения 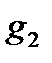, получаем конкретный вид передаточной функции:

Рисунок 3.14: Переходный процесс в фильтре при различных значениях .

По полученным графикам видно, что значение параметра 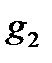 определяет установившееся значение выхода фильтра. При этом с ростом  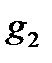установившееся значение выхода увеличивается. Так же видно, что  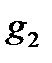существенно влияет на время переходного процесса.

⇐ Предыдущая1234Следующая ⇒

Поделиться: