Проверка гипотезы о значимости выборочного коэффициента корреляции
Пусть двумерная генеральная совокупность 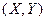 распределена по нормальному закону. Из этой совокупности извлечена выборка объема n и по ней найден выборочный коэффициент корреляции
распределена по нормальному закону. Из этой совокупности извлечена выборка объема n и по ней найден выборочный коэффициент корреляции 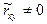 . Выборочный коэффициент является оценкой для коэффициента корреляции
. Выборочный коэффициент является оценкой для коэффициента корреляции 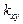 и, в общем случае, отличается от него; более того, между величинами
и, в общем случае, отличается от него; более того, между величинами 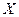 и
и 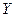 может отсутствовать корреляционная зависимость. Следовательно, в силу того, что выборка случайна, из того, что выборочный коэффициент корреляции
может отсутствовать корреляционная зависимость. Следовательно, в силу того, что выборка случайна, из того, что выборочный коэффициент корреляции 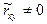 нельзя заключить, что коэффициент корреляции
нельзя заключить, что коэффициент корреляции 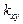 генеральной совокупности также отличен от нуля. Возникает необходимость при заданном уровне значимости
генеральной совокупности также отличен от нуля. Возникает необходимость при заданном уровне значимости 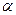 проверить нулевую гипотезу
проверить нулевую гипотезу 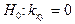 при конкурирующей гипотезе
при конкурирующей гипотезе 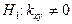 .
.
Если нулевая гипотеза 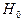 отвергается, то это будет означать, что выборочный коэффициент корреляции является значимым (выборочный коэффициент корреляции значимо отличается от нуля), а случайные величины X и Y коррелированны, т.е. связаны корреляционной зависимостью. Если нулевая гипотеза
отвергается, то это будет означать, что выборочный коэффициент корреляции является значимым (выборочный коэффициент корреляции значимо отличается от нуля), а случайные величины X и Y коррелированны, т.е. связаны корреляционной зависимостью. Если нулевая гипотеза 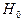 будет принята, то это будет означать, что выборочный коэффициент корреляции не является значимым, а случайные величины X и Y некоррелируемы. В качестве критерия возьмем случайную величину
будет принята, то это будет означать, что выборочный коэффициент корреляции не является значимым, а случайные величины X и Y некоррелируемы. В качестве критерия возьмем случайную величину
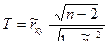 . (7.7.1)
. (7.7.1)
Известно (в случае нормального распределения (X, Y)), что эта случайная величина распределена по закону Стьюдента с 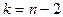 степенями свободы. В силу того, что распределение Стьюдента является симметричным, критическую область удобно брать симметричной:
степенями свободы. В силу того, что распределение Стьюдента является симметричным, критическую область удобно брать симметричной: 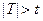 кр. Критическая точка
кр. Критическая точка 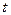 кр находится по таблице критических точек распределения Стьюдента, по заданному уровню значимости и числу степеней свободы
кр находится по таблице критических точек распределения Стьюдента, по заданному уровню значимости и числу степеней свободы 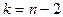 . Затем вычисляют (по данным выборки)
. Затем вычисляют (по данным выборки) 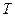 наб
наб 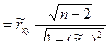 . Если
. Если 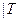 наб
наб 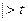 кр – нулевую гипотезу отвергают. Если
кр – нулевую гипотезу отвергают. Если 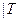 наб
наб 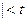 кр, нет оснований отвергать нулевую гипотезу.
кр, нет оснований отвергать нулевую гипотезу.
Задача 7.7.1. По выборке объемом n = 8 из двумерной генеральной совокупности (X, Y), распределенной по нормальному закону, в задаче 7.5.1 найден выборочный коэффициент корреляции 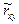 = 0,945. При уровне значимости
= 0,945. При уровне значимости 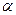 = 0,05 проверить нулевую гипотезу
= 0,05 проверить нулевую гипотезу 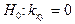 при альтернативной гипотезе
при альтернативной гипотезе 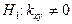 .
.
Решение. По уровню значимости 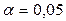 и числу степеней свободы
и числу степеней свободы 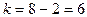 распределения Стьюдента (7.7.1) находим
распределения Стьюдента (7.7.1) находим 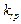 по табл. 8 критических точек распределения Стьюдента (для двусторонней критической области):
по табл. 8 критических точек распределения Стьюдента (для двусторонней критической области): 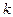 кр = 2,45. Вычисляем наблюдаемое значение критерия по формуле (7.7.1):
кр = 2,45. Вычисляем наблюдаемое значение критерия по формуле (7.7.1): 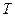 наб
наб 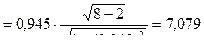 ;
; 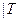 наб
наб 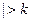 кр, следовательно, нулевая гипотеза
кр, следовательно, нулевая гипотеза 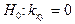 отвергается; случайные величины X и Y коррелированны.
отвергается; случайные величины X и Y коррелированны.
Задача 7.7.2. По выборке объемом n = 150 из двумерной генеральной совокупности (X, Y), распределенной по нормальному закону, найден выборочный коэффициент корреляции 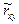 = 0,7. При уровне значимости
= 0,7. При уровне значимости 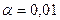 проверить нулевую гипотезу
проверить нулевую гипотезу 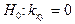 при альтернативной гипотезе
при альтернативной гипотезе 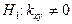 .
.
Решение. Вычислим сначала наблюдаемое значение критерия: 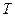 наб
наб 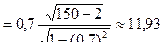 . Критическая точка
. Критическая точка 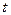 кр может быть найдена по табл. 8 приложения по
кр может быть найдена по табл. 8 приложения по 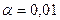 и числу степеней свободы
и числу степеней свободы 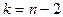 = 148; имеем
= 148; имеем 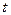 кр=2,58.
кр=2,58. 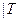 наб
наб 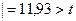 кр
кр 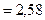 . Отсюда делаем вывод: нулевая гипотеза отвергается. Следовательно, выборочный коэффициент корреляции
. Отсюда делаем вывод: нулевая гипотеза отвергается. Следовательно, выборочный коэффициент корреляции 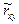 является значимым; между X и Y существует корреляционная связь.
является значимым; между X и Y существует корреляционная связь.
7.8. Проверка гипотезы о распределении генеральной совокупности.
Критерий c2 Пирсона
Проверка гипотезы о предполагаемом законе неизвестного закона распределения проводится так же, как и проверка гипотезы о параметрах распределения, т. е. с помощью специально подобранного критерия.
Критерий согласия – это критерий для проверки гипотезы о предполагаемом законе неизвестного распределения. Имеется несколько критериев согласия о проверке гипотезы о нормальном распределении генеральной совокупности – c2 Пирсона, Колмогорова – Смирнова и др.
Рассмотрим критерий c2, введенный Пирсоном (1900 г.). Пусть по выборке объема n получено статистическое распределение:
Таблица 7.8.1
Пусть нулевая гипотеза 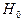 состоит в том, что генеральная совокупность X распределена по некоторому закону с функцией распределения
состоит в том, что генеральная совокупность X распределена по некоторому закону с функцией распределения 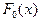 . Требуется при уровне значимости a проверить эту гипотезу.
. Требуется при уровне значимости a проверить эту гипотезу.
Согласно критерию Пирсона, выборочные данные следует представить в виде табл. 7.8.2:
Таблица 7.8.2
В табл. 7.8.2 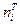 - теоретические частоты, соответствующие значению
- теоретические частоты, соответствующие значению 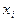 выборочной совокупности. На основании табл. 7.8.2 построим критерий (Пирсона):
выборочной совокупности. На основании табл. 7.8.2 построим критерий (Пирсона):
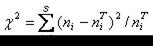 . (7.8.1)
. (7.8.1)
Эмпирические частоты 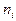 находятся из опыта. Как найти теоретические частоты
находятся из опыта. Как найти теоретические частоты 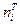 ? Предлагается следующее. Разобьем интервал наблюдаемых значений
? Предлагается следующее. Разобьем интервал наблюдаемых значений 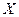 на s непересекающихся интервалов
на s непересекающихся интервалов 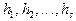 . Значения
. Значения 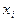 и экспериментальные частоты
и экспериментальные частоты 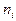 , соответствующие интервалу
, соответствующие интервалу 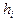 , будем считать определенными табл. 7.8.1. Положим
, будем считать определенными табл. 7.8.1. Положим 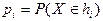 ; эти вероятности вычисляются с помощью гипотетического закона распределения
; эти вероятности вычисляются с помощью гипотетического закона распределения 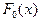 (или
(или 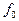 (x)) генеральной совокупности X. Тогда
(x)) генеральной совокупности X. Тогда
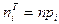 . (7.8.2)
. (7.8.2)
Тогда выражение для критерия (7.8.1) можно переписать в следующем виде:
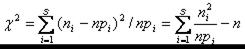 . (7.8.3)
. (7.8.3)
К. Пирсон доказал, что при 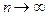 независимо от того по какому закону распределена генеральная совокупность
независимо от того по какому закону распределена генеральная совокупность 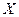 , случайная величина (7.8.1) или (7.8.3) стремится по распределению к закону распределения c2 с
, случайная величина (7.8.1) или (7.8.3) стремится по распределению к закону распределения c2 с 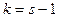 степенями свободы в случае полностью определенного гипотетического распределения, т.е. закон распределения не содержит неизвестных параметров. Плотность распределения c2 имеет вид
степенями свободы в случае полностью определенного гипотетического распределения, т.е. закон распределения не содержит неизвестных параметров. Плотность распределения c2 имеет вид
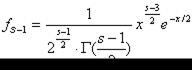 ,
, 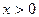 . (7.8.4)
. (7.8.4)
Задаем уровень значимости a. По уровню значимости 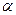 и числу степеней свободы
и числу степеней свободы 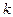 найдем c2 кр правосторонней критической области по табл. 7 критических точек для распределения c2. Затем по данным выборки по формуле (7.8.1) или (7.8.3) найдем наблюдаемые значения c2 наб.
найдем c2 кр правосторонней критической области по табл. 7 критических точек для распределения c2. Затем по данным выборки по формуле (7.8.1) или (7.8.3) найдем наблюдаемые значения c2 наб.
Если c2 наб> c2 кр, гипотеза 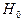 о предполагаемом распределении отвергается как не согласующаяся с опытными данными; если же c2 наб< c2 кр, то гипотеза
о предполагаемом распределении отвергается как не согласующаяся с опытными данными; если же c2 наб< c2 кр, то гипотеза 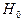 о предполагаемом распределении принимается.
о предполагаемом распределении принимается.
Задача 7.8.1. При 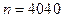 бросаниях монеты Бюффон получил
бросаниях монеты Бюффон получил 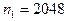 выпаданий «герба» и
выпаданий «герба» и 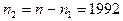 выпадений «решки». Совместимы ли эти данные с гипотезой
выпадений «решки». Совместимы ли эти данные с гипотезой 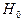 о биномиальном распределении генеральной совокупности с p = 1 / 2, т.е. с гипотезой о том, что монета была «правильной»?
о биномиальном распределении генеральной совокупности с p = 1 / 2, т.е. с гипотезой о том, что монета была «правильной»?
Решение. Выбираем уровень значимости 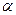 = 0,05. Выборочные данные представляем в виде следующей таблицы:
= 0,05. Выборочные данные представляем в виде следующей таблицы:
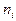
| 2048
| 1992
|
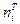
| 2020
| 2020
|
Здесь 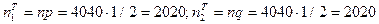 .
.
Составляем критерий 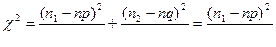 . (7.8.5)
. (7.8.5)
Согласно вышеизложенному, критерий c2 (7.8.5) приближенно подчиняется распределению c2 с одной 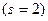 степенью свободы. С помощью табл. 7 приложения критических значений распределения c2 по уровню значимости a=0,05 числу степеней свободы
степенью свободы. С помощью табл. 7 приложения критических значений распределения c2 по уровню значимости a=0,05 числу степеней свободы 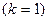 определим c2кр = 3,8. С другой стороны, с помощью формулы (7.8.5) определим наблюдаемое значение критерия c2наб
определим c2кр = 3,8. С другой стороны, с помощью формулы (7.8.5) определим наблюдаемое значение критерия c2наб 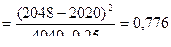 . c2наб <c2кр. Следовательно, нет основания отвергнуть нулевую гипотезу Н0, она принимается.
. c2наб <c2кр. Следовательно, нет основания отвергнуть нулевую гипотезу Н0, она принимается.
Случай вполне определенного гипотетического распределения встречается очень редко. Значительно чаще встречаются случаи, когда гипотетическое распределение содержит некоторое количество неизвестных параметров. При этом задается закон распределения генеральной совокупности известной математической формулой, но содержащей 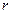 неизвестных параметров
неизвестных параметров 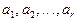 . Нулевая гипотеза, которую надлежит проверить, заключается в том, что генеральная совокупность имеет это гипотетическое распределение при некоторых значениях параметров
. Нулевая гипотеза, которую надлежит проверить, заключается в том, что генеральная совокупность имеет это гипотетическое распределение при некоторых значениях параметров 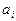 .
.
Как и раньше, наша выборка разбита на s групп, соответствующих s непересекающимся интервалам 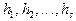 ; обозначим соответствующие частоты
; обозначим соответствующие частоты 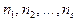 и соответствующие вероятности через рi (а1, а2,..., аr). Если бы «истинные» значения параметров
и соответствующие вероятности через рi (а1, а2,..., аr). Если бы «истинные» значения параметров 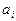 были известны, мы вычислили бы величину
были известны, мы вычислили бы величину
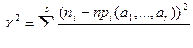 (7.8.6)
(7.8.6)
и применили бы критерий, описанный ранее в этом параграфе. Однако в настоящем случае значения параметров 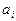 неизвестны и должны быть оценены по выборке. Тогда, если заменить в (7.8.6) параметры
неизвестны и должны быть оценены по выборке. Тогда, если заменить в (7.8.6) параметры 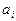 их оценками, то p i уже не будут постоянными, а будут функциями от выборки, и мы не сможем применить теорему о предельном распределении критерия c2 в силу того, что существует бесконечное множество различных возможных методов оценки параметров
их оценками, то p i уже не будут постоянными, а будут функциями от выборки, и мы не сможем применить теорему о предельном распределении критерия c2 в силу того, что существует бесконечное множество различных возможных методов оценки параметров 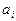 и свойства распределения (7.8.6) будут зависеть от выбранного метода. Проблема нахождения предельного распределения c2 при этих усложнениях условия впервые была рассмотрена Р. Фишером (1922-1924 гг.), который показал, что в этом случае необходимо изменить предложенное К. Пирсоном предельное распределение. Для ряда важных классов оценок изменение, предложенное Р. Фишером, имеет очень простой вид: необходимо лишь уменьшить число степеней предельного распределения (7.8.4), распределения c2 на столько единиц, каково число параметров, оцениваемых по выборке. Таким образом, предельное распределение c2 в этом случае имеет число
и свойства распределения (7.8.6) будут зависеть от выбранного метода. Проблема нахождения предельного распределения c2 при этих усложнениях условия впервые была рассмотрена Р. Фишером (1922-1924 гг.), который показал, что в этом случае необходимо изменить предложенное К. Пирсоном предельное распределение. Для ряда важных классов оценок изменение, предложенное Р. Фишером, имеет очень простой вид: необходимо лишь уменьшить число степеней предельного распределения (7.8.4), распределения c2 на столько единиц, каково число параметров, оцениваемых по выборке. Таким образом, предельное распределение c2 в этом случае имеет число 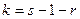 степеней свободы. Если предполагаемое распределение – нормальное,
степеней свободы. Если предполагаемое распределение – нормальное, 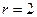 ; поэтому
; поэтому 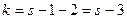 . Если предполагаемое распределение – распределение Пуассона,
. Если предполагаемое распределение – распределение Пуассона, 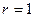 ,
, 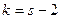 .
.
Задача 7.8.2. В книге «Математические методы статистики» Г. Крамер приводит следующие данные распределения размеров 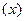 ,
, 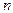 = 12000 бобов.
= 12000 бобов.
| Номер интервала
| 1
| 2
| 3
| 4
| 5
| 6
| 7
| 8
| 9
| 10
| 11
| 12
| 13
| 14
| 15
| 16
|
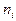
| 32
| 103
| 239
| 624
| 1187
| 1650
| 1883
| 1930
| 1638
| 1130
| 737
| 427
| 221
| 110
| 57
| 32
|
В таблице первый интервал – значения 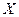 , меньшие 7,00 мм, второй – 7,00 – 7,25, третий – 7,25 – 7,50 и т.д. Проверить, согласуется ли размер бобов в выборке, предполагая, что этот признак в генеральной совокупности распределен по нормальному закону. Уровень значимости
, меньшие 7,00 мм, второй – 7,00 – 7,25, третий – 7,25 – 7,50 и т.д. Проверить, согласуется ли размер бобов в выборке, предполагая, что этот признак в генеральной совокупности распределен по нормальному закону. Уровень значимости 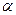 принят равным a = 0,01.
принят равным a = 0,01.
Решение. 1. Найдем выборочное среднее 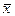 и «исправленное» среднее квадратическое отклонение
и «исправленное» среднее квадратическое отклонение 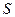 :
: 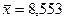 ;
; 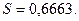 2. Находим величины npi для каждого из интервалов. Покажем, как это делается на примере второго интервала
2. Находим величины npi для каждого из интервалов. Покажем, как это делается на примере второго интервала 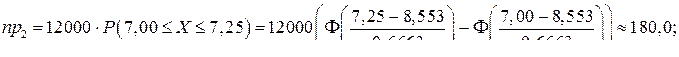 здесь значения функции Лапласа
здесь значения функции Лапласа 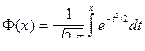 вычисляются по табл. 4 приложения. В результате получим ряд теоретических частот.
вычисляются по табл. 4 приложения. В результате получим ряд теоретических частот.
| Номер интервала
| 1
| 2
| 3
| 4
| 5
| 6
| 7
| 8
| 9
| 10
| 11
| 12
| 13
| 14
| 15
| 16
|
| 120
| 180,0
| 385,2
| 672,0
| 1082,4
| 1477,2
| 1700,4
| 1797,6
| 1568,4
| 1254,0
| 829,2
| 502,8
| 252,0
| 114,0
| 43,2
| 15,6
|
Находим наблюдаемое значение критерия c2 (7.8.6):
c2 наб 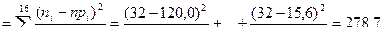 .
.
По табл. 7 приложения по уровню значимости 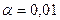 и числу степеней свободы
и числу степеней свободы 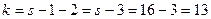 находим c2 кр.
находим c2 кр. 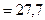 , очевидно, c2 наб > c2 кр, поэтому нулевая гипотеза
, очевидно, c2 наб > c2 кр, поэтому нулевая гипотеза 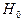 о том, что генеральная совокупность
о том, что генеральная совокупность 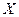 распределена по нормальному закону, отвергается.
распределена по нормальному закону, отвергается.
7.9. Сравнение генеральных средних двух распределенных по нормальному закону случайных величин. Сравнение генеральных средних двух произвольно распределенных случайных величин
(большие независимые выборки)
Метод статистических гипотез часто используется в тех случаях, когда на основании результатов выборочных наблюдений над двумя случайными величинами (генеральными совокупностями), распределенными по нормальному или произвольному закону, требуется ответить на вопрос, различаются ли их генеральные средние.
1. Пусть X и Y - генеральные совокупности с нормальным законом распределения с известными дисперсиями. На основании выборки объемом m из генеральной совокупности X и выборки объемом n генеральной совокупности получены выборочные средние 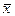 и
и 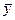 . Требуется по выборочным средним и уровню значимости
. Требуется по выборочным средним и уровню значимости 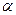 проверить нулевую гипотезу о том, что генеральные средние рассматриваемых совокупностей X и Y равны между собой:
проверить нулевую гипотезу о том, что генеральные средние рассматриваемых совокупностей X и Y равны между собой:
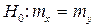 . (7.9.1)
. (7.9.1)
Такая задача ставится потому, что, как правило, выборочные средние оказываются различными и поэтому возникает вопрос, значимо или незначимо различаются выборочные средние.
Если нулевая гипотеза 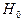 справедлива, т.е. генеральные средние одинаковы, то различие выборочных средних незначимо и объясняется случайными причинами, в частности, непредставительной выборкой объектов. Если же нулевая гипотеза отвергнута, т.е. генеральные средние неодинаковые, то различия
справедлива, т.е. генеральные средние одинаковы, то различие выборочных средних незначимо и объясняется случайными причинами, в частности, непредставительной выборкой объектов. Если же нулевая гипотеза отвергнута, т.е. генеральные средние неодинаковые, то различия 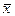 и
и 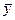 значимо и не может быть объяснено случайными причинами.
значимо и не может быть объяснено случайными причинами.
В качестве критерия примем следующую случайную величину:
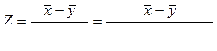 . (7.9.2)
. (7.9.2)
Случайная величина 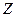 является нормальной нормированной случайной величиной с законом распределения
является нормальной нормированной случайной величиной с законом распределения 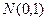 . Действительно,
. Действительно, 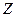 распределена по нормальному закону как линейная комбинация нормально распределенных случайных величин
распределена по нормальному закону как линейная комбинация нормально распределенных случайных величин 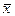 и
и 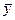 ; кроме того
; кроме того
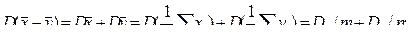
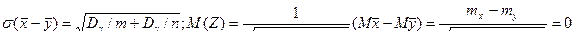 .
.
Вид критической области зависит от вида конкурирующей гипотезы.
Двусторонняя критическая область
Пусть 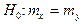 ; конкурирующая гипотеза
; конкурирующая гипотеза 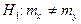 . Задаем уровень значимости a.
. Задаем уровень значимости a.
Двусторонняя критическая область определяется из условия, чтобы вероятность попадания критерия в эту область в предположении справедливости нулевой гипотезы была равна a.
Левую и правую критические точки выбираем из условий:
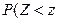 лев.кр.
лев.кр. 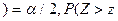 прав.кр.
прав.кр. 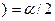 .
.
В силу симметричности закона распределения 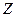 критические точки
критические точки 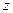 лев.кр и
лев.кр и 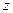 прав.кр симметричны относительно
прав.кр симметричны относительно 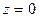 и обозначаются соответственно
и обозначаются соответственно 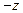 кр и
кр и 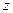 кр (рис. 7.9.1), поэтому задача сводится к нахождению zкр.
кр (рис. 7.9.1), поэтому задача сводится к нахождению zкр.

Рис. 7.9.1
Так как 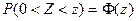 , где
, где 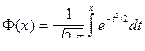 – функция Лапласа,
– функция Лапласа,
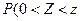 кр
кр 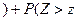 кр
кр 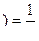 ,
, 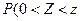 кр
кр 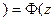 кр
кр 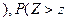 кр
кр 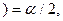 то
то
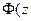 кр
кр 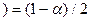 . (7.9.3)
. (7.9.3)
Из равенства (7.9.3) по табл. 4 приложения находим 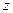 кр. Таким образом, двусторонняя критическая область определяется неравенствами:
кр. Таким образом, двусторонняя критическая область определяется неравенствами:
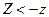 кр,
кр, 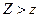 кр.
кр.
По формуле (7.9.3) и результатам выборки 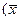 и
и 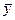 ), а также известным Dх и Dy, определим
), а также известным Dх и Dy, определим 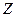 наб.
наб.
Если 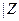 наб|>zкр нулевую гипотезу
наб|>zкр нулевую гипотезу 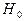 отвергают; если
отвергают; если 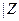 наб|<zкр – нет оснований отвергнуть нулевую гипотезу.
наб|<zкр – нет оснований отвергнуть нулевую гипотезу.
Задача 7.9.1. Изучается различие в среднем росте студентов мужского пола 1‑го и 2-го курса одного университета по двум независимым выборкам измерений роста на 1-м и 2-м курсах соответственно объемом 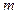 =50,
=50, 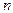 =60. Получены выборочные средние
=60. Получены выборочные средние 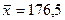 см,
см, 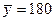 см. «Исправленные» выборочные дисперсии равны соответственно
см. «Исправленные» выборочные дисперсии равны соответственно 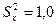 см,
см, 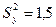 см. При уровне значимости
см. При уровне значимости 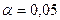 определить, значимо ли различаются выборочные средние значения роста студентов.
определить, значимо ли различаются выборочные средние значения роста студентов.
Решение. Критическое значение критерия 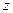 кр найдем по формуле (7.9.3) и табл. 4 приложения для функции Лапласа
кр найдем по формуле (7.9.3) и табл. 4 приложения для функции Лапласа 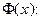
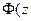 кр
кр 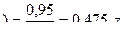 кр
кр 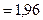 .
.
Наблюдаемое значение критерия найдем по данным выборки задачи и формуле (7.9.2):
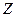 наб.
наб. 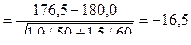 .
.
Так как 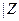 наб
наб 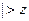 кр, то при уровне значимости
кр, то при уровне значимости 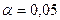 нулевую гипотезу
нулевую гипотезу 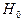 отвергаем, т.е. выборочные средние роста студентов различаются значимо.
отвергаем, т.е. выборочные средние роста студентов различаются значимо.
Правосторонняя критическая область
Пусть 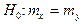 , но конкурирующая гипотеза
, но конкурирующая гипотеза 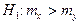 . Такой случай имеет место, если профессиональные соображения позволяют предположить, что генеральное среднее одной совокупности X больше генеральной средней другой совокупности Y (например, если усовершенствованная технология приводит к увеличению объема выпуска продукции, увеличению производительности труда и т.д.). В этом случае речь идет о правосторонней критической области, определяемой из условия
. Такой случай имеет место, если профессиональные соображения позволяют предположить, что генеральное среднее одной совокупности X больше генеральной средней другой совокупности Y (например, если усовершенствованная технология приводит к увеличению объема выпуска продукции, увеличению производительности труда и т.д.). В этом случае речь идет о правосторонней критической области, определяемой из условия
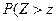 кр
кр 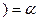 . (7.9.4)
. (7.9.4)
Так как 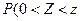 кр
кр 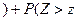 кр
кр 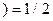 , то
, то
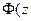 кр.
кр. 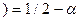 . (7.9.5)
. (7.9.5)
zкр находим из формулы (7.9.5) с помощью табл. 4 приложения; таким образом, правосторонняя критическая область определяется неравенством: Z> zкр (рис.7.9.2).

Рис. 7.9.2
По данным выборки и данным задачи определяем наблюдаемое значение критерия 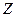 наб (при условии
наб (при условии 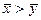 ). Если
). Если 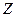 наб
наб 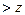 кр, нулевая гипотеза отвергается, если
кр, нулевая гипотеза отвергается, если 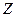 наб
наб 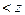 кр, нет оснований отвергнуть нулевую гипотезу
кр, нет оснований отвергнуть нулевую гипотезу 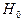 .
.
Левосторонняя критическая область
В данном случае нулевая гипотеза 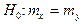 проверяется при конкурирующей гипотезе
проверяется при конкурирующей гипотезе 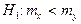 . В этом случае речь идет о левосторонней критической области (рис. 7.9.3), определяемой равенством
. В этом случае речь идет о левосторонней критической области (рис. 7.9.3), определяемой равенством
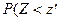 кр
кр 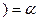 . (7.9.6)
. (7.9.6)

Рис. 7.9.3
В силу симметричности распределения 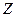 относительно
относительно 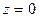 заключаем, что точка
заключаем, что точка 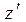 кр симметрична такой точке
кр симметрична такой точке 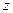 кр
кр 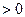 , что
, что 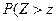 кр
кр 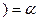 , т.е.
, т.е. 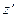 кр
кр 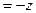 кр.
кр.
Следовательно, чтобы найти 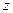 кр, находим сначала «вспомогательную» точку
кр, находим сначала «вспомогательную» точку 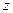 кр по равенству
кр по равенству 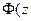 кр
кр 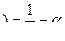 , а затем берем
, а затем берем 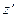 кр
кр 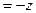 кр.
кр.
После нахождения наблюдаемого значения критерия 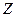 наб по данным выборки сравним его с
наб по данным выборки сравним его с 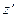 кр.
кр.
Если 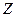 наб
наб 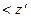 кр, нулевая гипотеза
кр, нулевая гипотеза 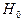 отвергается; если
отвергается; если 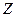 наб
наб 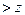 кр – нулевая гипотеза принимается.
кр – нулевая гипотеза принимается.
2. Пусть теперь требуется сравнить генеральные средние двух произвольно распределенных совокупностей X и Y, причем дисперсии их неизвестны, и пусть независимые выборки их имеют большой объем 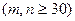 . Требуется проверить при заданном уровне значимости
. Требуется проверить при заданном уровне значимости 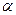 нулевую гипотезу
нулевую гипотезу 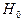
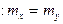 .
.
В этом случае (при больших m и n) выборочные средние 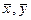 распределены приближенно нормально, а выборочные дисперсии
распределены приближенно нормально, а выборочные дисперсии 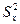 и
и 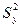 являются достаточно хорошими оценками дисперсии
являются достаточно хорошими оценками дисперсии 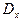 и
и 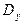 . Поэтому в качестве критерия можно взять следующую случайную величину:
. Поэтому в качестве критерия можно взять следующую случайную величину:
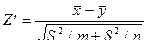 . (7.9.7)
. (7.9.7)
Эта случайная величина распределена приближенно по нормальному закону с параметрами 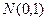 (при условии справедливости нулевой гипотезы). Критические области (двусторонние и односторонние) находятся так же, как и в n.1 этого подраздела.
(при условии справедливости нулевой гипотезы). Критические области (двусторонние и односторонние) находятся так же, как и в n.1 этого подраздела.
Критерий 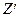 (7.9.7) также может быть использован и в случае нормального распределения генеральных совокупностей, но с неизвестными дисперсиями для выборок большого объема.
(7.9.7) также может быть использован и в случае нормального распределения генеральных совокупностей, но с неизвестными дисперсиями для выборок большого объема.
Задача 7.9.2. Произведено две выборки объемом m = 100 из генеральной совокупности X и n = 100 из генеральной совокупности Y. Найдены выборочные средние 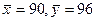 , а также «исправленные» выборочные дисперсии
, а также «исправленные» выборочные дисперсии 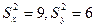 . Проверить с уровнем значимости
. Проверить с уровнем значимости 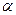 = 0,01 нулевую гипотезу о равенстве генеральных средних.
= 0,01 нулевую гипотезу о равенстве генеральных средних.
Решение. Пусть нулевая гипотеза 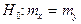 при конкурирующей гипотезе
при конкурирующей гипотезе 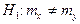 . В этом случае речь идет о двусторонней критической области. Имеем в виду критерий
. В этом случае речь идет о двусторонней критической области. Имеем в виду критерий
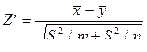 .
.
Эта случайная величина распределена приближенно по нормальному закону с параметрами 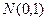 (при условии справедливости нулевой гипотезы). Критические области (двусторонние и односторонние) находятся так же, как и в n.1 этого подраздела.
(при условии справедливости нулевой гипотезы). Критические области (двусторонние и односторонние) находятся так же, как и в n.1 этого подраздела.
Критерий 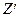 (7.9.7) также может быть использован и в случае нормального распределения генеральных совокупностей, но с неизвестными дисперсиями для выборок большого объема.
(7.9.7) также может быть использован и в случае нормального распределения генеральных совокупностей, но с неизвестными дисперсиями для выборок большого объема.
Задача 7.9.2. Произведено две выборки объемом m = 100 из генеральной совокупности X и n = 100 из генеральной совокупности Y. Найдены выборочные средние 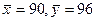 , а также «исправленные» выборочные дисперсии
, а также «исправленные» выборочные дисперсии 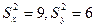 . Проверить с уровнем значимости
. Проверить с уровнем значимости 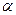 = 0,01 нулевую гипотезу о равенстве генеральных средних.
= 0,01 нулевую гипотезу о равенстве генеральных средних.
Решение. Пусть нулевая гипотеза 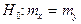 при конкурирующей гипотезе
при конкурирующей гипотезе 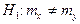 . В этом случае речь идет о двусторонней критической области. Имеем в виду критерий
. В этом случае речь идет о двусторонней критической области. Имеем в виду критерий
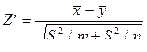 .
.
Отметим, что он распределен приближенно по закону 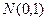 . Критическую точку
. Критическую точку 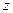 кр определим с помощью следующей приближенной формулы по табл. 4 приложения:
кр определим с помощью следующей приближенной формулы по табл. 4 приложения: 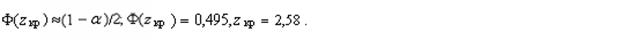
Найдем наблюдаемое значение критерия: 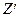 наб
наб  . Итак,
. Итак, 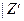 наб
наб 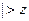 кр; нулевая гипотеза о равенстве генеральных средних отвергается.
кр; нулевая гипотеза о равенстве генеральных средних отвергается.

