
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
| НСВ | |||
| МОМЕНТ: | |||
| Начальный | 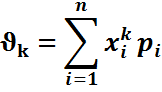
|
| |
| центральный | 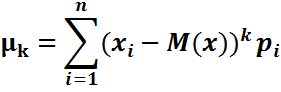
|
| |
Для более подробного описания распределения служат моменты высших порядков. Третий центральный момент 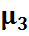 служит для характеристики асимметрии (скошенности распределения). Чтобы получить безразмерную величину ее делят на
служит для характеристики асимметрии (скошенности распределения). Чтобы получить безразмерную величину ее делят на 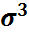 , где
, где 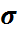 – среднее квадратическое отклонения случайной величины Х. Полученная величина А называется коэффициентом асимметрии случайной величины:
– среднее квадратическое отклонения случайной величины Х. Полученная величина А называется коэффициентом асимметрии случайной величины: 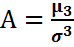 .
.
Четвертый центральный момент 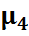 служит для характеристики крутости распределения. Эксцессом случайной величины называется число Е:
служит для характеристики крутости распределения. Эксцессом случайной величины называется число Е:
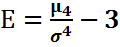 . Если Е<0 – кривая более островершинная. Если Е>0 – кривая более плосковершинная.
. Если Е<0 – кривая более островершинная. Если Е>0 – кривая более плосковершинная.
Биноминальный закон распределения. Мат ожидание и дисперсия св распределенной по биноминальному закону.
Определение: Дискретная св Х имеет биноминальный закон распределения, если она принимает знач 0,1,2…, m,…, n с вероятностями P(X=m)=  , где 0<p<1, q=1 – p, m=0,1,…,n. Следовательно биноминал закон распределения представляет собой закон распределения X=m наступления события А в n независимых испыт, в каждом из которых оно может произойти с одной и той же вероятностью p. Теорема . Математическое ожидание числа появлений события
, где 0<p<1, q=1 – p, m=0,1,…,n. Следовательно биноминал закон распределения представляет собой закон распределения X=m наступления события А в n независимых испыт, в каждом из которых оно может произойти с одной и той же вероятностью p. Теорема . Математическое ожидание числа появлений события  в
в  независимых испытаниях равно произведению числа испытаний на вероятность появления события
независимых испытаниях равно произведению числа испытаний на вероятность появления события  в каждом испытании, которая вычисляется по формуле: M ( X )= np . Теорема. Дисперсия числа появлений события
в каждом испытании, которая вычисляется по формуле: M ( X )= np . Теорема. Дисперсия числа появлений события  в
в  независимых испытаниях равна произведению числа испытаний на вероятности появления и не появления события
независимых испытаниях равна произведению числа испытаний на вероятности появления и не появления события  в одном испытании: Д(Х)= npq .
в одном испытании: Д(Х)= npq .
Закон распределения Пуассона. Мат ожидание и дисперсия св, распределенной по закону Пуассона.
Определение: дискретная св Х имеет закон распределения Пуассона, если она принимает значения 0,1,2, … , m, … (бесконечное, но счетное множество значений) с вероятностями P ( X = m )=  , где m=0,1,2, …;
, где m=0,1,2, …;  . Теорема. Мат ожидание и дисперсия св, распределенной по закону Пуассона, совпадают и равны параметру
. Теорема. Мат ожидание и дисперсия св, распределенной по закону Пуассона, совпадают и равны параметру  этого закона, т.е. М(Х)=
этого закона, т.е. М(Х)=  , Д(Х)=
, Д(Х)=  .
.
Сл событ и их клас. Алгебра событий. Частота и вероят
Одним из основных понятий тв яв понятие события. Случайным событием (возможным событием или просто событием) называется любой факт, который в результате испытания может произойти или не произойти. Под испытанием (опытом, экспериментом) в этом определении понимается выполнение определенного комплекса условий, в которых наблюдается то или иное явление, фиксируется тот или иной результат. Событие – это не какое-нибудь происшествие, а лишь возможный исход, результат испытания (опыта эксперимента), обозначается прописными (заглавными) буквами латинского алфавита. События называются несовместными (несовместимыми), если наступление одного из них исключает наступление любого другого. В противном случае события называются совместными (совместимыми). Событие называется достоверным, если в результате испытания оно обязательно должно произойти. Событие называется невозможным, если в результате испытания оно вообще не может произойти. События называются равновозможными, если в результате испытания по условиям симметрии ни одно из этих событий не является объективно более возможным. Несколько событий называются единственно возможными, если в результате испытания обязательно должно произойти хотя бы одно из них. Несколько событий образуют полную группу (полную систему), если они являются единственно возможными и несовместимыми исходами испытания. Это означает, что в результате испытания обязательно должно произойти одно и только одно из этих событий. Частным случаем событий, образующих полную группу, являются противоположные события – два несовместных события, из которых одно должно обязательно произойти. Алгебра событий: задано произвольное, но фиксированное пространство элементарных событий  , которое можно представить в виде некоторой области на плоскости. При этом элементарные события
, которое можно представить в виде некоторой области на плоскости. При этом элементарные события  – это точки плоскости, лежащие внутри
– это точки плоскости, лежащие внутри  . Поскольку событие отождествляется с множеством, то над событиями можно совершать все операции, выполнимые над множествами. То есть, по аналогии с теорией множеств, строится алгебра событий. В частности, определены следующие операции и отношения между событиями: 1)
. Поскольку событие отождествляется с множеством, то над событиями можно совершать все операции, выполнимые над множествами. То есть, по аналогии с теорией множеств, строится алгебра событий. В частности, определены следующие операции и отношения между событиями: 1)  (
(  ) –сумма событий. Это событие, состоящее в том, что произошло хотя бы одно из двух событий
) –сумма событий. Это событие, состоящее в том, что произошло хотя бы одно из двух событий 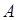 или
или  (не исключающее логическое «или»);– событие, состоящее в появлении хотя бы одного из этих событий; 2)
(не исключающее логическое «или»);– событие, состоящее в появлении хотя бы одного из этих событий; 2)  (
(  ) –произведение событий. Это событие, состоящее в совместном осуществлении событий
) –произведение событий. Это событие, состоящее в совместном осуществлении событий 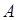 и
и  (логическое «и»); – событие, состоящее в одновременном осуществлении всех этих событий. Таким образом, события
(логическое «и»); – событие, состоящее в одновременном осуществлении всех этих событий. Таким образом, события 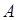 и
и  несовместны, если произведение их есть событие невозможное, т.е.
несовместны, если произведение их есть событие невозможное, т.е.  ; 3)
; 3)  (множество элементов, принадлежащих
(множество элементов, принадлежащих 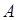 , но не принадлежащих
, но не принадлежащих  ) – разность событий. Это событие, состоящее из исходов, входящих в
) – разность событий. Это событие, состоящее из исходов, входящих в 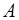 , но не входящих в
, но не входящих в  . Оно заключается в том, что происходит событие
. Оно заключается в том, что происходит событие 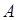 , но при этом не происходит событие
, но при этом не происходит событие  ; 4) Противоположным (дополнительным) для события
; 4) Противоположным (дополнительным) для события 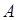 (обозначается
(обозначается 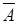 ) называется событие, состоящее из всех исходов, которые не входят в
) называется событие, состоящее из всех исходов, которые не входят в 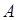 . Два события называются противоположными, если появление одного из них равносильно не появлению другого.Численная мера степени объективной возможности наступления события называется вероятностью события.
. Два события называются противоположными, если появление одного из них равносильно не появлению другого.Численная мера степени объективной возможности наступления события называется вероятностью события.
2. Классическое определение вероят связано с определением благоприят-его исхода. Исход назыв благоприятствующим данному событию, если его появление влечет за собой наступление этого события. Вероят событ 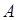 = отношению числа равновозможных благоприятст-их элементар исходов к общему числу всех равновозможных и единственно возможных элементарных исходов данного испытания:
= отношению числа равновозможных благоприятст-их элементар исходов к общему числу всех равновозможных и единственно возможных элементарных исходов данного испытания:  ,где
,где  – число благоприятствующих событию
– число благоприятствующих событию 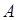 исходов;
исходов;  – общее число возможных исходов. Из определения вероят события
– общее число возможных исходов. Из определения вероят события 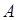 следует, что
следует, что 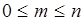 , поэтому всегда выполняются неравенства
, поэтому всегда выполняются неравенства  , т.е. вероят любого события есть неотрицат число, не превышающее 1 . Если
, т.е. вероят любого события есть неотрицат число, не превышающее 1 . Если  , то событие
, то событие 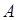 невозможное. Если
невозможное. Если  , то событие
, то событие 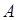 достоверное. Равновозможные элементар события яв равновероятными, т.е. обладают одной и той же вероят.
достоверное. Равновозможные элементар события яв равновероятными, т.е. обладают одной и той же вероят.
3.Статистич определ вероят. Классич определ вероят не яв пригодным для изучения произвольных случайных событий. Так, оно неприемлемо, если результ испыт не равновозможны. Во многих случаях более удобным оказывается статист опред вероят, кот связано с понятием относител частоты появления события  в опытах. Относительная частота (частость) появления события
в опытах. Относительная частота (частость) появления события  – это отнош числа
– это отнош числа  появлений события
появлений события 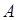 в серии из
в серии из  опытов к числу испытан. При однотипных массовых испыт во многих случаях наблюдается устойчивость относительной частоты события, т.е. с увеличением числа испытаний в сериях относительная частота
опытов к числу испытан. При однотипных массовых испыт во многих случаях наблюдается устойчивость относительной частоты события, т.е. с увеличением числа испытаний в сериях относительная частота  колеблется около некоторого постоянного числа
колеблется около некоторого постоянного числа  , причем эти отклонения тем меньше, чем дольше произведено испыт, если не учитывать отдельные неудачные испыт (выбросы). Вероят событ
, причем эти отклонения тем меньше, чем дольше произведено испыт, если не учитывать отдельные неудачные испыт (выбросы). Вероят событ  в статистич смысле назыв число
в статистич смысле назыв число  , относительно кот устанав (стабилизируется) относит частота
, относительно кот устанав (стабилизируется) относит частота  при неогранич увеличении числа опытов. Относит частота вычис по форм:
при неогранич увеличении числа опытов. Относит частота вычис по форм: 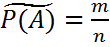 . Под вероят события в статист смысле понимается почти достоверный предел его относит частоты при неограниченно растущем числе испыт. Таким образом, почти достоверно, что относит частота события приближенно совпадает с его статистич вероятностью, если число испыт достаточно велико. Свойства (св-ва вероят, вытекающие из классич определен вероят, сохраняются и при статистич определении вероят): 1) рассматриваемые события должны быть исходными только тех испыт, кот могут быть воспроизведены неограничен число раз при одном и том же комплексе условий; 2) событ должны обладать статистич устойчивостью; 3) число испыт должно быть достаточно велико. Достаточно малую вероят, при кот наступлен событ можно счит практически невозможным, наз уровнем значимости. При широких предположен доказывается, что вероятн события в классич и статистич смыслах совпадают.
. Под вероят события в статист смысле понимается почти достоверный предел его относит частоты при неограниченно растущем числе испыт. Таким образом, почти достоверно, что относит частота события приближенно совпадает с его статистич вероятностью, если число испыт достаточно велико. Свойства (св-ва вероят, вытекающие из классич определен вероят, сохраняются и при статистич определении вероят): 1) рассматриваемые события должны быть исходными только тех испыт, кот могут быть воспроизведены неограничен число раз при одном и том же комплексе условий; 2) событ должны обладать статистич устойчивостью; 3) число испыт должно быть достаточно велико. Достаточно малую вероят, при кот наступлен событ можно счит практически невозможным, наз уровнем значимости. При широких предположен доказывается, что вероятн события в классич и статистич смыслах совпадают.
4.Аксиоматич определен вероятн. Геометрич определ вероятн. Наиболее распространенной в настоящее время яв логическая схема построения основ теории вероятностей, кот была разработана А.Н.Колмогоровым в 1933 году. Основные черты этой схемы следующие: при изучении какой-либо задачи методами теории вероятностей, прежде всего, выделяется множество  , называемое пространством элементарных исходов. Элементы
, называемое пространством элементарных исходов. Элементы  этого множества составляют совокупность возможных исходов наблюдения – элементарных событий. Всякое случайное событие описывается совокупностью благоприятствующих ему элементарных исходов и, поэтому, рассматривается как множество элементарных событий. Некоторые из этих случайных событий образуют борелево множество
этого множества составляют совокупность возможных исходов наблюдения – элементарных событий. Всякое случайное событие описывается совокупностью благоприятствующих ему элементарных исходов и, поэтому, рассматривается как множество элементарных событий. Некоторые из этих случайных событий образуют борелево множество  наблюдаемых событий
наблюдаемых событий  , каждому из кот сопоставлено некотор определен число
, каждому из кот сопоставлено некотор определен число  , т.е. на
, т.е. на  задана функция множеств. Аксиомы: 1.
задана функция множеств. Аксиомы: 1. 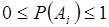 ; 2.
; 2.  , т.е. вероятность достоверного события равна единице; 3. Вероятность события
, т.е. вероятность достоверного события равна единице; 3. Вероятность события 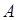 , заключающееся в том, что наступит одно из попарно несовместных событий
, заключающееся в том, что наступит одно из попарно несовместных событий  (
(  ), составляет
), составляет  . Эти условия составляют аксиомы теории вероятностей. Геометрическая вероятность события А – отношение меры области благоприятствующих появлению события к мере всей области, т.е.
. Эти условия составляют аксиомы теории вероятностей. Геометрическая вероятность события А – отношение меры области благоприятствующих появлению события к мере всей области, т.е. 
Последнее изменение этой страницы: 2019-05-08; Просмотров: 234; Нарушение авторского права страницы