
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Мат ожидание дискретной и непрерывной св и их св-ва
Мат ожидание характеризует среднее ожидаемое значение св, т.е. приближенно равно ее среднему знач (вероятностный смысл математического ожидания). Математическое ожидание характеризует положение св на числовой оси и принимается за среднее значение, вокруг кот происходит разброс возможных значений св. При малом разбросе возможных значений случайной величины относительно ее математического ожидания можно им пренебречь и считать, что данная величина полностью характеризуется ее математическим ожиданием, т.е. она неслучайна. Если же математическое ожидание мало, а разброс велик, то пренебрежение им, т.е. неучет случайности данной величины, приведет к недопустимым ошибкам. Математическим ожиданием для дискретной случайной величины X называется сумма произведений всех ее значений на соответствующие им вероятности, определяется по данной формуле: Свойства математического ожидания для дискретных и непрерывных случайных величин: 1. Мат ожидание постоянной величины С равно постоянной величине, т.е. M ( C ) = C . 2. Постоянный множитель можно вынести за знак мат ожидания, т.е. M ( CX )= CM ( X ). 3. Мат ожидание суммы св равно сумме их мат ожиданий, т.е. M ( x 1 +………..+ xn )= M ( x 1 )+………….+ M ( xn ). 4. Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий, т.е. M ( x 1 × …. × xn )= M ( x 1 ) × …. × M ( xn ). 18. Дисперсия св и ее свойства. На практике часто требуется оценить рассеяние св вокруг ее среднего значения. Использовать в качестве такой характеристики отклонение Доказательство . Действительно, учитывая, что M(X) – постоянная величина, имеем: Дисперсия для непрерывной св: Свойства дисперсии: 1) Дисперсия постоянной величины равна нулю, т.е. Д(С)=0. 2) Постоянный множитель можно вынести за знак дисперсии, возводя его в квадрат, т.е. Д(СХ)=С2Д(Х). 3) Дисперсия суммы независимых случайных величин есть сумма их дисперсий, т.е. Д(х1+…+ xn )=Д(х1)+…+Д(х n ). 19. Корреляц момент и коэфт корреляции и их свойства. Определение. Корреляцией (или коррел моментом) 1. ковариация двух независимых св равна 0. 2. ковариация 2 св = мат ожиданию их произведения минус произведение их математических ожиданий. 3. ковариация двух св по абсолютной величине не превосходит произведения их средних квадратических отклонений. Ковариация, как уже отмечено, характеризует не только степень зависимости двух св, но и их разброс, рассеяние. Кроме того, она – величина размерная, ее размерность определяется произведением размерностей св. Это затрудняет испол ковариации для оценки степени зависимости для различных св. Этих недостатков лишен коэф корреляции. Определение. Коэффициент корреляции двух случайных величин называется отношение их ковариации к произведению средних квадратичсеких отклонений этих величин: 1. Коэф корреляции прин знач на отрезке [-1;1], т.е. -1 £ 3. Если коэф корреляции двух св = (по абсолютной величине) 1 (или вообще отличен от нуля), то между этими св существует линейная функциональная зависимость. 20.Моменты случайной величины. Ассиметрия и эксцесс. Среди числовых характеристик случайных величин особое значение имеют моменты: начальные и центральные. Начальным моментом k-ого порядка случайной величины Х яв мат ожидание k-ой степени этой величины, т.е. ДСВ | НСВ | |||||
| МОМЕНТ: | ||||||
| Начальный | 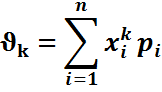
|
| ||||
| центральный | 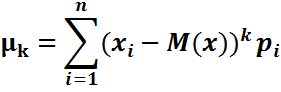
|
| ||||
Для более подробного описания распределения служат моменты высших порядков. Третий центральный момент 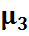 служит для характеристики асимметрии (скошенности распределения). Чтобы получить безразмерную величину ее делят на
служит для характеристики асимметрии (скошенности распределения). Чтобы получить безразмерную величину ее делят на 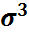 , где
, где 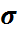 – среднее квадратическое отклонения случайной величины Х. Полученная величина А называется коэффициентом асимметрии случайной величины:
– среднее квадратическое отклонения случайной величины Х. Полученная величина А называется коэффициентом асимметрии случайной величины: 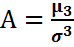 .
.
Четвертый центральный момент 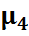 служит для характеристики крутости распределения. Эксцессом случайной величины называется число Е:
служит для характеристики крутости распределения. Эксцессом случайной величины называется число Е:
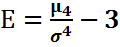 . Если Е<0 – кривая более островершинная. Если Е>0 – кривая более плосковершинная.
. Если Е<0 – кривая более островершинная. Если Е>0 – кривая более плосковершинная.
Последнее изменение этой страницы: 2019-05-08; Просмотров: 241; Нарушение авторского права страницы