Теорема сложения вероятностей. Теорема. Сумма вероятностей событий, образующих полную группу

Теорема. Вероятность суммы несовместных событий равна сумме вероятностей этих событий: .

Теорема. Сумма вероятностей событий, образующих полную группу, равна единице: P(A)+P(B)+…+P(K)=1.

Теорема. Сумма вероятностей противоположных событий равна единице: P(A)+P( =1.

6. Условная вероятность. Теорема умножения вероят. Определение: Условной вероятностью события B при условии, что событие А уже произошло, называется число, которое обозначается: P(B/A)=P_A(B). Определение: Два события наз независимыми, если появление одного из них не влияет на вероятность появления другого события, в противном случае зависимыми. Теорема: вероятность произведения двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие наступило. P(AB)=P(A) P(B/A). Следствие: вероятность произведения n-зависимых событий равна произведению вероятности одного из них события на условную вероятность всех остальных событий, при чем вероятность каждого последующего события выполняется в предположении, что все предыдущие произошли: P(A₁×A₂×…×A_n)=P(A₁) ×  ×  Следствие: вероятность суммы двух совместных событий равна сумме вероятностей этих событий без вероятности их произведения: P(A+B)=P(A)+P(B)-P(A×B). Теорема: вероятность произведения двух независимых событий равна произведению вероятностей этих событий: P(AB)=P(A) ×P(B).

 

7. Формула полной вероятности. Формула Байеса. Следствием 2 основ теорем вероятн – теоремы сложен и умнож – яв формула полной вероят и формула Байеса. Теорема: если событие А может произойти только при условии появлен одного из событий-гипотез Н₁, Н₂, …, Н_n, образующих полную группу, то вероятн события А равна сумме произведен вероят каждого из этих событий на соответствующие усл вероятн: P(A)= . Условная вероятн гипотезы  при условии того, что событие А произошло, определяется по формуле вероятности гипотез или формуле Байеса (она позволяет пересмотреть вероятн гипотез после пересмотрения вероятности событ А) и определ по формуле: P(H_i/A)= . Значен формулы Байеса состоит в том, что по мере получения новой информации, можно проверять и корректировать выдвинутые до испытан гипотезы. Такой подход, называемый байесовским, дает возможность корректировать управлен решения в экономике, оценки неизвестных параметров распределен изучаемых признаков в статистич анализе и т.п.

 

8. Повторные независ испыт. Форм Бернулли. Если вероят наступлен событ А в каждом испыт не меняется в зависимос от исходов других, то такие испыт наз независим относител событ А. Ели независим повтор испыт проводятся при одном и том же комплексе условий, то вероят наступлен событ А в каждом испыт одна и та же. Описанная последовательн независимых испыт получила назван схемы Бернулли. Серия повторных независимых испыт, в каждом из кот данное событие  имеет одну и ту же вероят , не зависящую от номера испыт, наз схемой Бернулли. Таким образом, в схеме Б для каждого испыт имеются только 2 исхода: событие  (успех), вероят кот  и событие  (неудача), вероят кот . Теорема. Если вероят p наступления события А в каждом испыт постоянна, то вероятность P_m,n того, что событие А наступит m раз в n независимых испыт равна: P_{m,n = 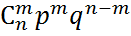,} где q=1 – p.

9. Наивероятнейшее число наступлений события. Число наступлений события  наз наивероятнейшим, если оно имеет наибольшую вероятность по сравнению с вероятностями наступления  любое другое количество раз. Определение: число m₀ наступления события А в n независимых испытан наз наивероятнейшим, если вероятность осуществления этого события по крайней мере не меньше вероятности других событий при любом m. Теорема. Наивероятнейшее число наступлений события  в  независимых испытаниях заключено между числами  и : .

 

 

10. Теорема Пуассона. Простейший поток событий.  С увеличением  чаще всего испол схему П. Эта схема яв предельным случаем схемы Бернулли, в кот предполагается, что вероят 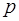 события  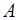не яв постоянной, а зависит от числа испыт  таким образом, что величина 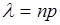 остается постоянной. В этом случае оценка вероятности того, что событ  наступит  раз, определяется предельной теоремой Пуассона. Теорема: Если вероятность 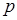 наступления событ  в каждом испыт постоянна и мала, а число независимых испытаний  достаточно велико, то вероятность того, что событие  наступит  раз, приближенно равна или если вероятность p наступления события А в каждом испытании стремится к 0 при неограниченном увеличении числа n-испытаний, причем n×p®l, то вероят p того, что событие А появится m раз в n независимых испыт удовлетворяет предельному равенству: , где 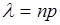. Если вероят мала, а количество испытаний большое, то применяют приближенные формулы для вычисления вероят l=np<20. Формула Пуассона находит применен в теории массового обслуживания. Особенностью вероятностной схемы Пуассона является то, что для определения вероятности того или иного числа успехов не требуется знать ни , ни 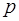. Все определяется, в конечном счете, числом , которое является ни чем иным, как средним числом успехов. Формулу Пуассона можно считать математической моделью простейшего потока событий с интенсивностью .

Потоком событий называют последовательность событий, которые наступают в случайные моменты времени. Интенсивностью потока  называют среднее число событий, которые появляются в единицу времени. Простейшим (пуассоновским) называют поток событий, который обладает свойствами стационарности, отсутствия последствий и ординарности. Свойство стационарности характеризуется тем, что вероятность  появления  событий на любом промежутке времени зависит только от числа  и от длительности промежутка времени  и не зависит от начала его отсчёта, т.е., если поток событий стационарный, то вероятность  есть функция, зависящая только от числа  и от длительности . Свойство отсутствия последствия характеризуется тем, что вероятность появления  событий на любом промежутке времени не зависит от того, появлялись или не появлялись события в моменты времени, предшествующие началу рассматриваемого промежутка. Потоку событий присуще свойство отсутствия последствий, если имеет место взаимная независимость появления того или иного числа событий в непересекающиеся промежутки времени. Свойство ординарности характеризуется тем, что появление двух и более событий за малый промежуток времени практически невозможно. Ординарность потока событий означает, что за бесконечно малый промежуток времени может появиться не более одного события.

 

11. Локальная теорема Муавра – Лапласа Предположим, что в условиях схемы Бернулли проводится  испыт, в результ каждого из кот с вероят  ( ) происходит событ . Интегральная теорема Муавра-Лапласа содержит приближенную формулу для вероятности P_n(a,b) того, что событие 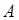 появится не менее а раз и не более b раз. С ростом количества испытаний числа a и b растут, а вероятность  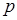постоянна. Интегральная теорема Муавра-Лапласа: Если вероятность p наступления события А в каждом испытании постоянна и отлична от 0 и 1, то вероятность того, что число m наступления события А в n независимых испытаниях заключено в пределах от а до b (включительно), при достаточно большом числе n (или: вероятность того, что число m появления события А в схеме Бернулли находится в заданном промежутке от а до b, при большом числе испытаний n) приблизительно равна: P(a £ m £ b) » , где Ф(x)= 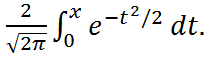  Чем больше n, тем точнее эта формула. При выполнении условия npq³20 интегральная формула, так же как и локальная, дает незначительную погрешность вычисления вероятностей. Функция Ф(x) табулирована. Свойства функции Ф( x ): 1) Функция Ф(x) нечетная, т.е. Ф(–x)= – Ф(x); 2) Функция Ф(x) монотонно возрастающая, причем при x®+¥ Ф(x)®1 (практически можно сказать, что уже при x>4 Ф(x)»1) .

12. Интегральная теорема Муавра - Лапласа. Лаплас получил важную приближенную формулу для вероятности  появления события 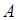 точно  раз, при условии, что  достаточно велико. Теорема. Пусть  – вероятность события 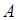, причем . Тогда вероятность того, что в условиях схемы Бернулли событие 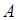 при  испытаниях появится точно  раз, выражается приближенной формулой Лапласа: 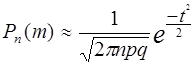, где ; .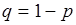

Локальная теорема Муавра-Лапласа: если вероятность p наступления события А в каждом испытании постоянна и отлична от о и 1, то вероятность P_n(m) того, что событие А произойдет m раз в n независимых испытаниях при достаточно большом числе n, приближенно равна: 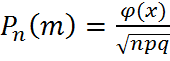, где ;  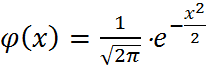Чем больше n, тем точнее приближенная формула, вычисления дают незначительную погрешность, когда npq³20. Для упрощения расчетов, связанных с применением формулы, составлена таблица значений функции .

Свойства функции

1. Функция  четной, т.е.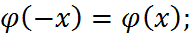

2. Функция  – монотонно убывающая при положительных значениях x, причем при x®¥  ®0 (практически можно считать, что уже при x>4  »0) .

 

13. Функция распределения случайной величины и ее свойства. Как для дискретной величины, так и для непрерывной вводится понятие функции распределения. Пусть  – случайная величина, определенная на множестве элементарных событий 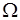, , а  – произвольное действительное число. В общем случае функция  должна быть такова, чтобы для любых  событие , состоящее в том, что случайная величина  попадает в интервал , принадлежала полю событий и, таким образом, для любого такого события была определена вероятность . Тогда вероятность того, что  примет значение, меньшее, чем , равна значению функции распределения вероятностей данной случайной величины , соответствующее значению аргумента , т.е. функция распределения вероятностей данной случайной величины  представляет собой вероятность события , где  – задаваемые непрерывно изменяющиеся значения, т.е. .

⇐ Предыдущая12345Следующая ⇒

Поделиться: