Траектории линейных систем на плоскости.
Рассмотрим автономную линейную однородную систему  (3) с постоянными коэффициентами. Будем полагать n = 2 и
(3) с постоянными коэффициентами. Будем полагать n = 2 и  . В этом предположении система имеет единственное положение равновесия в начале координат. С помощью линейного неособого преобразования X = SY приведем систему (3) к виду
. В этом предположении система имеет единственное положение равновесия в начале координат. С помощью линейного неособого преобразования X = SY приведем систему (3) к виду  ,
,
где J — жорданова форма матрицы A. В зависимости от вида собственных чисел имеют место следующие случаи:
1) 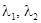 вещественны, различны и
вещественны, различны и  . В этом случае
. В этом случае  . Параметрические уравнения траекторий таковы:
. Параметрические уравнения траекторий таковы:  . Координатные полуоси являются траекториями, соответствующими
. Координатные полуоси являются траекториями, соответствующими  или
или  . При
. При  и
и 
 .
.
Картина расположения траекторий при  , имеющая специальное название — узел, изображена на рис. 1а.
, имеющая специальное название — узел, изображена на рис. 1а.
2) 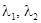 вещественны и
вещественны и  . Полученные в случае узла формулы сохраняют силу. Соответствующая геометрическая картина, называемая седлом, изображена на рис. 1б.
. Полученные в случае узла формулы сохраняют силу. Соответствующая геометрическая картина, называемая седлом, изображена на рис. 1б.
3) 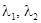 комплексно-сопряженные. Пусть
комплексно-сопряженные. Пусть  . В преобразовании X = SY
. В преобразовании X = SY 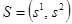 , где
, где  и
и  — линейно независимые собственные векторы, соответствующие
— линейно независимые собственные векторы, соответствующие  и
и 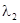 . Так как А вещественна,
. Так как А вещественна,  и
и  можно выбрать комплексно-сопряженными. Тогда и
можно выбрать комплексно-сопряженными. Тогда и  . Положим
. Положим  ,
,  , а в качестве фазовой плоскости возьмем
, а в качестве фазовой плоскости возьмем  . Переменная
. Переменная  связана с Х соотношением X = SY = = STZ = QZ, где
связана с Х соотношением X = SY = = STZ = QZ, где 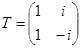 ,
,  . Следовательно, Q — вещественная неособая матрица. Преобразование приводит к виду
. Следовательно, Q — вещественная неособая матрица. Преобразование приводит к виду

где матрица коэффициентов образует вещественную жорданову форму матрицы А.
Введем полярные координаты 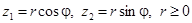 , или
, или  ,
,  . Имеем:
. Имеем:  . Отделяя вещественные и мнимые части, получим:
. Отделяя вещественные и мнимые части, получим:
 .
.
Следовательно,  . При
. При  траектории образуют спирали (рис. 1в). Такое положение траекторий называется фокусом. При
траектории образуют спирали (рис. 1в). Такое положение траекторий называется фокусом. При  все траектории — окружности. В этом случае получаем центр. В случае центра все решения системы (3) периодические с периодом 2p/b.
все траектории — окружности. В этом случае получаем центр. В случае центра все решения системы (3) периодические с периодом 2p/b.
4) 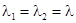 . Жорданова форма матрицы А имеет треугольный вид, а система преобразуется к виду
. Жорданова форма матрицы А имеет треугольный вид, а система преобразуется к виду
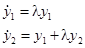
Решением этой системы будет функция  . В зависимости от формы матрицы J получаются два случая: или вырожденный узел (рис. 1г), либо звездный (дикритический) узел. Дикритический узел возможен лишь в случае системы
. В зависимости от формы матрицы J получаются два случая: или вырожденный узел (рис. 1г), либо звездный (дикритический) узел. Дикритический узел возможен лишь в случае системы 

Рис. 1. Поведение траекторий в зависимости от значений собственных чисел
1.5. Линейные однородные системы
с периодическими коэффициентами.
В данном пункте излагается так называемая теория Флоке.
Будем рассматривать систему вида  (4)
(4)
где 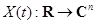 , а матричная функция P(t) удовлетворяет условию P(t + w) = P(t), w> 0 при всех
, а матричная функция P(t) удовлетворяет условию P(t + w) = P(t), w> 0 при всех  . Такие матричные функции будем называть периодическими с периодом w или w-периодическими.
. Такие матричные функции будем называть периодическими с периодом w или w-периодическими.
Теорема Флоке. Фундаментальная матрица системы (4) имеет вид
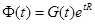
где G — w-периодическая матрица, R — постоянная матрица.
Матрица В, определяемая равенством 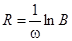 , называется матрицей монодромии. Для нее справедливо
, называется матрицей монодромии. Для нее справедливо  . Она определяется с помощью фундаментальной матрицы неоднозначно, но можно показать, что все матрицы монодромии подобны. Часто матрицей монодромии называют ту, которая порождается нормированной при
. Она определяется с помощью фундаментальной матрицы неоднозначно, но можно показать, что все матрицы монодромии подобны. Часто матрицей монодромии называют ту, которая порождается нормированной при  фундаментальной матрицей
фундаментальной матрицей 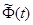 , то есть
, то есть  .
.
Собственные числа 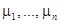 матрицы монодромии называются мультипликаторами уравнения (4), а собственные числа
матрицы монодромии называются мультипликаторами уравнения (4), а собственные числа  матрицы R — характеристическими показателями. Из определения R имеем
матрицы R — характеристическими показателями. Из определения R имеем  , при этом простым мультипликаторам соответствуют простые характеристические показатели, а кратным — характеристические показатели с элементарными делителями той же кратности.
, при этом простым мультипликаторам соответствуют простые характеристические показатели, а кратным — характеристические показатели с элементарными делителями той же кратности.
Характеристические показатели определены с точностью до  . Из
. Из  и формулы Лиувилля следует, что
и формулы Лиувилля следует, что  .
.
Название мультипликатор объясняется следующей теоремой:
Теорема. Число m является мультипликатором уравнения (4) тогда и только тогда, когда существует ненулевое решение 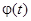 этого уравнения такое, что при всех t
этого уравнения такое, что при всех t  .
.
Следствие 1. Линейная периодическая система (4) имеет нетривиальное решение периода w тогда и только тогда, когда по меньшей мере один из ее мультипликаторов равен единице.
Следствие 2. Мультипликатору  соответствует так называемое антипериодическое решение
соответствует так называемое антипериодическое решение 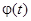 периода w, т. е.
периода w, т. е.  . Отсюда имеем:
. Отсюда имеем:

Таким образом, 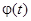 есть периодическое решение с периодом
есть периодическое решение с периодом  . Аналогично, если
. Аналогично, если  (p и q — целые,
(p и q — целые,  ), то периодическая система имеет периодическое решение с периодом
), то периодическая система имеет периодическое решение с периодом 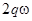 .
.
Пусть 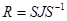 , где
, где  — матрица из теоремы Флоке,
— матрица из теоремы Флоке, 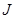 — ее жорданова форма. По теореме Флоке
— ее жорданова форма. По теореме Флоке  , или
, или  , (5)
, (5)
где  — фундаментальная матрица,
— фундаментальная матрица,  — w-периодическая матрица. В структуре фундаментальной матрицы линейной системы с периодическими коэффициентами характеристические показатели играют ту же роль, что и собственные числа матрицы коэффициентов в структуре фундаментальной матрицы линейной системы с постоянными коэффициентами.
— w-периодическая матрица. В структуре фундаментальной матрицы линейной системы с периодическими коэффициентами характеристические показатели играют ту же роль, что и собственные числа матрицы коэффициентов в структуре фундаментальной матрицы линейной системы с постоянными коэффициентами.
Пример. Рассмотрим дифференциальное уравнение второго порядка
 , (6)
, (6)
где  — w-периодическая вещественная скалярная функция. Мультипликаторами уравнения (6) будем называть мультипликаторы соответствующей линейной системы, т. е. системы
— w-периодическая вещественная скалярная функция. Мультипликаторами уравнения (6) будем называть мультипликаторы соответствующей линейной системы, т. е. системы
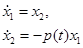
с матрицей  . Так как
. Так как  , то
, то 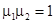 . Мультипликаторы являются собственными числами матрицы
. Мультипликаторы являются собственными числами матрицы
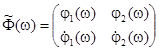 ,
,
где  — решение уравнения (6), удовлетворяющее начальным условиям
— решение уравнения (6), удовлетворяющее начальным условиям 
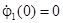 , а
, а  — решение уравнения (6), удовлетворяющее начальным условиям
— решение уравнения (6), удовлетворяющее начальным условиям 
 . Пусть
. Пусть  — характеристическое уравнение для определения мультипликаторов. Так как
— характеристическое уравнение для определения мультипликаторов. Так как  , то оно принимает вид
, то оно принимает вид  , где
, где  .
.
2. Устойчивость решений систем
дифференциальных уравнений.
Устойчивость по Ляпунову.
Вводя определение устойчивости по Лагранжу и Пуассону в пункте 1.3, описывались свойства одной отдельно взятой траектории. Понятие устойчивости по Ляпунову характеризует траекторию с точки зрения поведения соседних траекторий, располагающихся в ее окрестности. Предположим, что система при старте из начальной точки  порождает траекторию
порождает траекторию  . Рассмотрим другую траекторию той же системы
. Рассмотрим другую траекторию той же системы  , стартовая точка которой близка к
, стартовая точка которой близка к  . Если обе траектории остаются близкими в любой последующий момент времени, то траектория
. Если обе траектории остаются близкими в любой последующий момент времени, то траектория  называется устойчивой по Ляпунову.
называется устойчивой по Ляпунову.
Наглядная иллюстрация устойчивости по Лагранжу, Пуассону и Ляпунову приводится на рис. 2. Когда говорят просто об устойчивой траектории, то всегда имеется в виду устойчивость по Ляпунову.

Рис. 2. Качественная иллюстрация устойчивости по Лагранжу (траектория остается в замкнутой области), по Пуассону (траектория многократно возвращается в e-окрестность стартовой точки) и по Ляпунову (две близкие на старте траектории остаются близкими всегда)
Рассмотрим уравнение  (1)
(1)
где  и функция f удовлетворяет в G условию Липшица локально:
и функция f удовлетворяет в G условию Липшица локально:
 и
и  , где
, где  — константа, не зависящая от выбора точек
— константа, не зависящая от выбора точек  и
и  .
.
Предположим, что уравнение (1) имеет решение  , определенное при
, определенное при  , и что
, и что 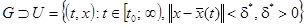 . Чтобы перейти к исследованию нулевого решения, выполним в (1) замену
. Чтобы перейти к исследованию нулевого решения, выполним в (1) замену  . В результате получим уравнение
. В результате получим уравнение
 , (2)
, (2)
где  определена в области, содержащей множество
определена в области, содержащей множество  . Это уравнение называется уравнением в отклонениях. Пусть
. Это уравнение называется уравнением в отклонениях. Пусть  — решение (2) с начальными данными
— решение (2) с начальными данными  .
.
Определение. Решение 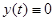 уравнения (2) называется устойчивым по Ляпунову, если для
уравнения (2) называется устойчивым по Ляпунову, если для  , такое, что при
, такое, что при 
 .
.
Решение 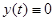 называется асимптотически устойчивым, если оно устойчиво по Ляпунову и существует
называется асимптотически устойчивым, если оно устойчиво по Ляпунову и существует  такое, что
такое, что  при
при  .
.
Неустойчивость решения  означает следующее: существуют положительное
означает следующее: существуют положительное  , последовательность начальных точек
, последовательность начальных точек  при
при 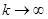 , и последовательность моментов времени
, и последовательность моментов времени  такие, что
такие, что  .
.
При исследовании вопроса об устойчивости решений часто прибегают к заменам переменных, позволяющим упростить вид рассматриваемого уравнения. Сделаем в (2) замену  , где функция
, где функция  определена при всех
определена при всех  и непрерывна по z при
и непрерывна по z при 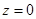 равномерно относительно
равномерно относительно  , причем
, причем  . Пусть уравнение
. Пусть уравнение  однозначно разрешимо относительно z:
однозначно разрешимо относительно z:  , где
, где  определена на множестве
определена на множестве  и непрерывна по y при
и непрерывна по y при  равномерно относительно
равномерно относительно  . Пусть уравнение (2) заменой
. Пусть уравнение (2) заменой  можно преобразовать в уравнение
можно преобразовать в уравнение  .
.
Лемма. При сделанных предположениях нулевое решение уравнения (2) устойчиво по Ляпунову, асимптотически устойчиво или неустойчиво тогда и только тогда, когда соответственно устойчиво по Ляпунову, асимптотически устойчиво или неустойчиво нулевое решение уравнения 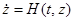 .
.
Пусть уравнение (2) автономно, а его нулевое решение асимптотически устойчиво. Множество  называется областью притяжения решения
называется областью притяжения решения 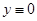 .
.

