Устойчивость линейных однородных систем.
Пусть  (3)
(3)
— вещественная система,  — ее произвольное решение. Замена
— ее произвольное решение. Замена 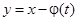 приводит (3) к виду
приводит (3) к виду 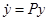 , т. е. произвольное решение уравнения (3) переводится в тривиальное решение того же уравнения. Следовательно, все решения уравнения (3) устойчивы по Ляпунову, асимптотически устойчивы или неустойчивы одновременно. Поэтому можно говорить об устойчивости уравнения (3), понимая под этим устойчивость всех его решений, в частности тривиального.
, т. е. произвольное решение уравнения (3) переводится в тривиальное решение того же уравнения. Следовательно, все решения уравнения (3) устойчивы по Ляпунову, асимптотически устойчивы или неустойчивы одновременно. Поэтому можно говорить об устойчивости уравнения (3), понимая под этим устойчивость всех его решений, в частности тривиального.
Лемма 1. Пусть  и
и 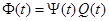 или
или 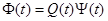 , где
, где 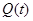 — неособая при всех
— неособая при всех  матрица, ограниченная по норме вместе с обратной
матрица, ограниченная по норме вместе с обратной  . Тогда
. Тогда  ограничена, не ограничена или бесконечно мала по норме при
ограничена, не ограничена или бесконечно мала по норме при 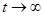 тогда и только тогда, когда
тогда и только тогда, когда 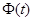 обладает таким свойством.
обладает таким свойством.
Лемма вытекает из оценки  .
.
Следствие. Пусть  ,
,  — нормированная при
— нормированная при 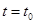 фундаментальная матрица уравнения (3). Любая фундаментальная матрица уравнения (3) ограничена, не ограничена или бесконечно мала по норме вместе с
фундаментальная матрица уравнения (3). Любая фундаментальная матрица уравнения (3) ограничена, не ограничена или бесконечно мала по норме вместе с  .
.
Теорема 1. 1) Для того чтобы уравнение (3) было устойчивым по Ляпунову, необходимо и достаточно, чтобы его фундаментальные матрицы были ограничены при  . 2) Для того чтобы уравнение (3) было асимптотически устойчивым, необходимо и достаточно, чтобы его фундаментальные матрицы были бесконечно малыми при
. 2) Для того чтобы уравнение (3) было асимптотически устойчивым, необходимо и достаточно, чтобы его фундаментальные матрицы были бесконечно малыми при  .
.
Доказательство. 1) Достаточность. Пусть  ограничена на
ограничена на 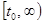 . Решение
. Решение  задается формулой
задается формулой 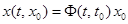 . (*)
. (*)
Так как 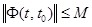 , то
, то  . Следовательно, уравнение (3) устойчиво по Ляпунову, так как устойчиво его тривиальное решение. Действительно, если
. Следовательно, уравнение (3) устойчиво по Ляпунову, так как устойчиво его тривиальное решение. Действительно, если 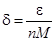 , то при всех
, то при всех 
 . (**)
. (**)
Необходимость. Пусть уравнение (3) устойчиво по Ляпунову. Тогда устойчиво его тривиальное решение, и выполняется (**). Пусть  фиксировано. Положим
фиксировано. Положим 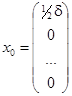 . Если
. Если  , то
, то  . Из (*) и (**) имеем
. Из (*) и (**) имеем  , т. е.
, т. е.  ограничена. Аналогично доказывается ограниченность
ограничена. Аналогично доказывается ограниченность 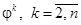 , а вместе с ними и матрицы
, а вместе с ними и матрицы  .
.
2) Достаточность. Пусть 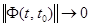 при
при  . В силу (*)
. В силу (*) 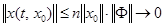 при всех
при всех 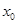 , что и дает асимптотическую устойчивость.
, что и дает асимптотическую устойчивость.
Необходимость. Пусть для любых  при
при  . Положим
. Положим 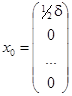 . В силу (*)
. В силу (*)  , следовательно,
, следовательно,  . Аналогично доказывается, что
. Аналогично доказывается, что 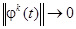 ,
,  , что означает
, что означает 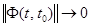 при
при  . Теорема доказана.
. Теорема доказана.
Применим теорему 1 к исследованию устойчивости уравнения (3) с постоянной матрицей коэффициентов P. Уравнение (3) в этом случае имеет фундаментальную матрицу 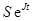 ,
,  , где
, где 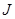 — жорданова форма матрицы P. По теореме 1, лемме 1 и следствию к ней устойчивость по Ляпунову, асимптотическая устойчивость и неустойчивость уравнения (3) эквивалентны соответственно ограниченности, бесконечной малости и неограниченности матрицы
— жорданова форма матрицы P. По теореме 1, лемме 1 и следствию к ней устойчивость по Ляпунову, асимптотическая устойчивость и неустойчивость уравнения (3) эквивалентны соответственно ограниченности, бесконечной малости и неограниченности матрицы 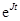 при
при  . Отсюда получаем следующую теорему:
. Отсюда получаем следующую теорему:
Теорема 2. Линейная однородная система с постоянным коэффициентами: 1) устойчива по Ляпунову тогда и только тогда, когда среди собственных чисел матрицы коэффициентов нет таких, вещественные части которых положительны, а число мнимые и нулевые собственные числа либо простые, либо имеют только простые элементарные делители; 2) асимптотически устойчива тогда и только тогда, когда все собственные числа матрицы коэффициентов имеют отрицательные вещественные части.
Ниже рассматриваются необходимые и достаточные условия отрицательности корней характеристического уравнения линейной однородной системы с постоянными коэффициентами — критерий Гурвица (Рауса-Гурвица), а также частотный критерий Михайлова, являющийся геометрическим признаком, эквивалентным критерию Гурвица.
Определение. Полином  , где
, где  ,
, 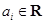 ,
,  называется полиномом Гурвица, если все его корни имеют отрицательные вещественные части.
называется полиномом Гурвица, если все его корни имеют отрицательные вещественные части.
Если полином  является полиномом Гурвица, то все
является полиномом Гурвица, то все  .
.
Составим 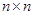 -матрицу Гурвица вида
-матрицу Гурвица вида

Теорема Гурвица (критерий Гурвица). Для того чтобы полином 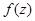 являлся полиномом Гурвица, необходимо и достаточно, чтобы были положительны все главные диагональные миноры его матрицы Гурвица
являлся полиномом Гурвица, необходимо и достаточно, чтобы были положительны все главные диагональные миноры его матрицы Гурвица  :
:
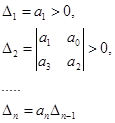
Если степень полинома  сравнительно большая, то применение критерия Гурвица становится затруднительным. В этом случае для определения расположения корней полинома
сравнительно большая, то применение критерия Гурвица становится затруднительным. В этом случае для определения расположения корней полинома 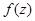 на комплексной плоскости иногда оказывается более удобным использование частотного критерия Михайлова.
на комплексной плоскости иногда оказывается более удобным использование частотного критерия Михайлова.
Определение. Пусть 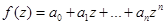 , где
, где  ,
,  ,
,  . Кривая
. Кривая  ,
, 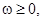 называется годографом Михайлова функции
называется годографом Михайлова функции  .
.
Критерий Михайлова непосредственно следует из леммы:
Лемма 2 . Угол поворота в положительном направлении ненулевого вектора 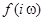 при
при 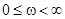 равен
равен  , где
, где 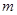 — число корней полинома
— число корней полинома  с положительной вещественной частью с учетом их кратностей.
с положительной вещественной частью с учетом их кратностей.
Критерий Михайлова. Для того чтобы полином  , не имеющий чисто мнимых корней, являлся полиномом Гурвица, необходимо и достаточно, чтобы угол поворота в положительном направлении вектора
, не имеющий чисто мнимых корней, являлся полиномом Гурвица, необходимо и достаточно, чтобы угол поворота в положительном направлении вектора  при
при  был бы равен
был бы равен 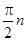 .
.
Замечание. Если полином  есть полином Гурвица степени
есть полином Гурвица степени 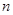 , то вектор
, то вектор 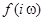 монотонно поворачивается в положительном направлении на угол
монотонно поворачивается в положительном направлении на угол 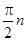 , то есть годограф Михайлова, выходя из точки
, то есть годограф Михайлова, выходя из точки 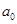 положительной полуоси
положительной полуоси  , последовательно пересекает полуоси
, последовательно пересекает полуоси 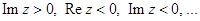 , проходя
, проходя 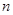 квадрантов.
квадрантов.

