
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Силы, вызывающие вибрацию корпуса суднаСтр 1 из 6Следующая ⇒
Силы, вызывающие вибрацию корпуса судна
Виды нагрузок, вызывающие вибрацию корпуса судна и его отдельных конструкций
Все нагрузки, вызывающие вибрацию корпуса корабля и его отдельных конструкций, целесообразно разделить на четыре вида. К первому виду отнесем меняющиеся во времени силы, которые появляются вследствие неточностей, допущенных при изготовлении и монтаже судовых механизмов, валопроводов, гребных винтов. Ко второму виду принадлежат нагрузки, связанные с тем, что гребные винты корабля работают за корпусом и в непосредственной близости от него. Третий вид нагрузок составляют силы, вызванные воздействием на судно морского волнения. Наконец, к четвертому виду будем относить различные динамические нагрузки, появляющиеся в специфических условиях эксплуатации судна: при взрывах, ударах о лед, ударах при швартовке и столкновениях и т.п. Нагрузки, вызванные работой гребных винтов за корпусом
Действие нагрузок, связанных с работой гребных винтов за корпусом в непосредственной близости от него, представляет собой наиболее существенную причину вибрации судна. Винт, работающий за корпусом судна, возбуждает два вида вибрационной нагрузки: нагрузку, передающуюся корпусу через подшипники и непосредственно приложенную к обшивке в виде пульсирующих давлений. Нагрузка, передающаяся корпусу через подшипники Неоднородность потока, набегающего на винт, создается вследствие нескольких причин, среди которых важнейшую роль играет так называемый попутный поток. Осевая Vx (направленная вдоль оси гребного вала) и окружная Vt составляющие скорости регулярной части попутного потока могут быть рассчитаны или измерены с использованием I модельного эксперимента. Осевую составляющую удобно представить в виде суммы:
Vx = v0 + vx,
где v0 - скорость судна; vx - зависящая от координат в плоскости диска винта составляющая осевой скорости. Пример изменения vx и Vt за один оборот лопасти двухвинтового судна показан на рис.1.3
Рис 1.3 Пример изменения vx/ v0 и Vt/ v0 за один оборот лопасти.
Местная вибрация корабля. Вибрация набора судового корпуса. Свободные колебания однопролётной свободно опёртой балки
Расчетная схема
Рис.2.1 Расчётная схема однопролётной свободно опёртой балки. Исходные данные
Дифференциальное уравнение свободных колебаний упругой системы
Учитывая даламберовы силы, дифференциальное уравнение свободных колебаний однопролётной балки имеет вид:
Общее решение колебаний упругой системы
Дифференциальное уравнение для форм главных свободных колебаний призматического стержня
где
Общий интеграл дифференциального уравнения для форм главных свободных колебаний Граничные условия на свободно опёртых концах балки
Граничные условия для рассматриваемого стержня имеют вид:
Внося сюда выражение (2.2), получаем граничные условия для форм свободных колебаний:
Составление уравнений из условий подчинения граничным условиям на левом и правом концах балки
Подчиняя выражение (2.5) граничным условиям (2.6) функции wk ( х ) при х = 0 и х = L получаем систему линейных однородных алгебраических уравнений относительно неизвестных постоянных Ak, Bk, Ck и D/ e:
Система линейных однородных алгебраических уравнений относительно неизвестных постоянных интегрирования
Расчёт и построение форм первых пяти тонов главных свободных колебаний свободно опёртого призматического стержня
Рис.2.2 Форма свободных колебаний однопролётной свободно опёртой балки.
Расчёт значений частот первых пяти тонов свободных колебаний свободно опёртого призматического стержня с удвоенным по сравнению с заданным значением интенсивности веса балки
Вычисление значения интенсивности массы самого призматического стержня с учетом удвоенного, по сравнению с заданным, значением интенсивности веса балки, а именно:
тогда частоты первых пяти тонов свободных колебаний (2.11) будут равны:
при k = 1: при k = 2: при k = 3: при k = 4: при k = 5:
Исходные данные для расчёта свободных колебаний гибких пластин
Исходные данные для исследования колебаний корпуса корабля однопролётной безопорной призматической балки
Исходные данные
Тип судна | |||||||||||||||||||||||||||||||||||||||||||||||||||
| танкеры | сухогрузы | контейнерные суда | ро-ро | ||||||||||||||||||||||||||||||||||||||||||||||||
| Продольные, kП Крутильные, kкр Вертикальные, kB Горизонтальные, kr | 33 63 5, 6-106 4, 95-106 | 33 58 5, 5∙ 106 3, 95∙ 106 | 33 55 5, 42∙ 106 3, 81∙ 106 | 33 60 3, 8∙ 106 3, 02∙ 106 | |||||||||||||||||||||||||||||||||||||||||||||||

5.4 Определение значений высших частот (второго, третьего и четвёртого тонов) свободных поперечных колебаний судового корпуса по формуле Центрального научно-исследовательского института имени академика А.Н. Крылова
Nn = cnN1, кол. /мин, (5.3)
где Nn - частота свободных колебаний n-го тона;
сп - числовой коэффициент, зависящий от номера тона, типа судна и вида рассматриваемых колебаний.
N1 = 1·48, 07 = 48, 01кол. /мин,
N2 = 2·48, 07 = 96, 14кол. /мин,
N3 = 3·48, 07 = 144, 21кол. /мин,
N4 = 4·48, 07 = 192, 28кол. /мин,
N5 =5·48, 07 = 240, 35кол. /мин,
5.5 Расчёт значений высших частот (второго, третьего и четвёртого тонов) свободных поперечных колебаний судового корпуса по рекомендациям Н.Н. Бабаева и В.Г. Лентякова
 (5.4)
(5.4)
N1 = 48, 07 кол. /мин,
N2 = 2, 2·48, 07 = 105, 74 кол. /мин,
N3 = 1, 8·96, 14 = 173, 05 кол. /мин,
N4 = 1, 5·144, 21 = 216, 31 кол. /мин.
5.6 Расчёт частоты свободных вертикальных колебаний первого тона судового корпуса по формуле Шлика для 5 вариантов значения длины корпуса корабля по отношению к заданному значению: 0.8; 1.0; 1.2; 1.4; 1.6

при 0, 8L: 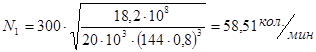 ,
,
при 1, 0L:  ,
,
при 1, 2L:  ,
,
при 1, 4L:  .
.
при 1, 6L:  .
.
5.7 Расчёт частоты свободных вертикальных колебаний первого тона судового корпуса по формуле Шлика для 5 вариантов значения интенсивности веса " q" корпуса корабля по отношению к заданному значению: 0.8; 1.0; 1.2; 1.4; 1.6
при 0, 8q:  ,
,
при 1, 0q:  ,
,
при 1, 2q:  ,
,
при 1, 4q:  ,
,
при 1, 6q:  ,
,
Сопоставление результатов расчётов значений частоты первого тона свободных колебаний корпуса корабля как свободного безопорного призматического стержня со значениями, определёнными по формулам Шлика и Шлика-Бюрилля
Сравнивая результаты расчетов значений частоты первого тона свободных колебаний корпуса корабля как свободного безопорного призматического стержня со значениями, определёнными по формулам Шлика и Шлика-Бюрилля видно, что при изменении длины и интенсивности веса корабля происходит изменение частоты первого тона свободных колебаний корпуса корабля. Чем больше длина и интенсивность веса корабля, тем меньше частота свободных колебаний корпуса корабля. Больше всего на частоту свободных колебаний корпуса корабля влияет длина корабля.
Литература
1. Ипатовцев Ю.Н., Короткин Я.И. Строительная механика и прочность корабля. Раздел IY Динамические задачи прочности корпуса: Учебник. Л.: Cудостроение, 1991
2. Постнов В.А., Калинин В.С., Ростовцев Д.М. Вибрация корабля: Учебник. - Л.: Cудостроение, 1983
3. Курдюмов А.А. Вибрация корабля: Учебник. Л.: Судпромгиз, 1961
4. Справочник по строительной механике корабля: в 3-х томах / Под ред. акад. Ю.А. Шиманского. Л.: Судпромгиз. 1960
Силы, вызывающие вибрацию корпуса судна
Последнее изменение этой страницы: 2019-10-04; Просмотров: 281; Нарушение авторского права страницы