Погашение основного долга равными выплатами

Пусть заем D выдан на n лет под i сложных годовых процентов. При рассматриваемом способе выплаты долга в конце каждого года выплачивается n-я доля основного долга, т.е. величина . В конце первого года, кроме того платятся проценты с суммы D, которой пользовались в течение этого года, т. е. iD. Весь платеж в конце первого года равен:

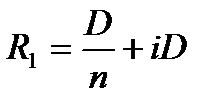. Основной долг при этом уменьшится на  и составит . В конце 2-го года выплата составит 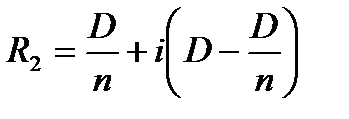 и т.д.

Пример. Заем величиной 5000у.е. выдан на 5 лет под сложные проценты 10% годовых. Составим план погашение задолженности с условием, что основной долг гасится равными выплатами.

Решение: Основной долг гасится равными выплатами: Процентные деньги за первый год составят 5000·0, 1=500 у.е. Таким образом, в конце первого года должник выплатит 1500 (1000+500) условных единиц. На начало второго года основной долг уменьшится на 1000 у.е. и составит 4000 у.е. Следовательно, процентные деньги за второй год составят 40000, 1=400 у.е. Вместе с суммой, направленной на погашение основного долга, это составит 1400 у.е., и т. д.

Таким образом, схема погашения долга следующая:

01                          2                          3                         4                        5                         1000              1000              1000              1000            1000                    +                     +                    +                    +                  +                        500                400                 300                200              100                     =                    =                     =                    =                  =                       1500              1400               1300           1200              1100

5000          4000              3000             2000               1000                0 0

Погашение займа равными годовыми выплатами

Пусть заем выдан на n лет под i сложных годовых процентов. При рассматриваемом способе его выплаты в конце каждого периода выплачивается одинаковая сумма R.

Выплаты R можно рассматривать как годовую ренту длительностью n лет с годовым платежом R. Приравняем современную величину этой ренты величине займа. Тогда коэффициент приведения ренты будет определён по формуле:

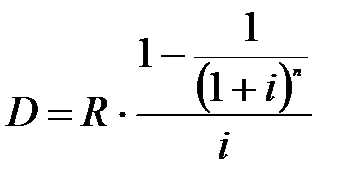, где                          (7.3)

Отсюда определим величину годового платежа:

.                                                   (7.4)

Пример. Заем 5000 у.е. выдан на 5 лет под сложные проценты 10% годовых. Найдите величину годового платежа, если долг должен быть погашен равными годовыми выплатами.

Решение:

.

1323

3779

,

0

500

6209

,

0

1

500

61051

,

1

1

1

500

1

,

1

1

1

1

,

0

5000

5

у.е.

R

=

=

-

=

-

=

-

×

=

 

Погашение займа равными выплатами несколько раз в год

 

Пусть выплаты размером Y производятся m раз в году в течение n лет. Тогда количество выплат составит mn. На эти выплаты начисляют проценты m раз в году по ставке . Выплаты образуют ренту. Ее наращенная величина может быть определена по формуле:

                        (7.5)

Пусть D – размер займа. Наращенная величина займа к концу срока составит:

                                    (7.6)

Составим уравнение эквивалентности, приравняв приведенные к концу срока финансовой операции величины займа и ренты:

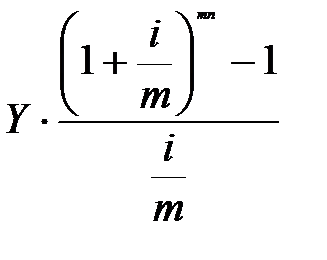= (7.7)

Из этого равенства определим размер выплаты :

        (7.8)

 

Пример. Заем в 10000 у.е. выдан на 3 года под 12 сложных годовых процентов. Выплаты производятся а) ежеквартально (m= 4) б) ежемесячно (m=12). Найти величину разовой выплаты.

Решение:

а)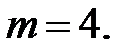

 

б)

.

 

Пример. Заем в 500 000 у.е. выданный на 5 лет под 10% сложных годовых, должен быть погашен ежеквартальными выплатами. Найти величину разовой выплаты.

Решение:

 

 

⇐ Предыдущая9101112131415161718Следующая ⇒

Поделиться: