Метод регуляризующего множителя для решения задачи Гильберта для аналитических функций в случае произвольной односвязной области

 

Дан простой гладкий замкнутый контур 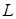, ограничивающий область , и действительные функции дуги  контура 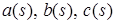 удовлетворяющие условию Гёльдера.

Краевую задачу Гильберта можно сформулировать так. найти аналитическую в области 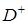 и непрерывную на контуре функцию , предельные значения действительной и мнимой части которой удовлетворяют на контуре 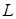 линейному соотношению

 

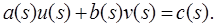 (3.1)

 

При 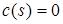 будем иметь однородную задачу и при 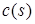, отличной от нуля, - неоднородную.

Оператор Шварца для односвязной области.

Часто приходится решать задачу об определении аналитической в области функции  по заданной на границе области действительной части . В дальнейшем будем эту задачу для краткости называть задачей Шварца. По  определяется гармоническая в области функция , а по ней интегрированием полного дифференциала (уравнения Коши - Римана) с точностью до произвольного слагаемого находится сопряженная гармоническая функция . Таким образом, задача Шварца решается с точностью до произвольного постоянного слагаемого. Решение будет вполне определенным, если задать в какой-либо точке области значение мнимой части искомой аналитической функции. Для решения задачи Шварца введем понятие оператора Шварца.

Под оператором Шварца будем понимать оператор, восстанавливающий аналитическую функцию по граничным значениям ее действительной части.

Пусть на гладком контуре  задана некоторая действительная функция 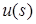, удовлетворяющая условию Гёльдера. Оператором Шварца  будем называть оператор, который определяет аналитическую функцию , предельное значение действительной части которой на контуре совпадает с функцией 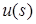, а мнимая часть в заданной точке  обращается в нуль.

Символически это будем записывать так:

 

 

Если контур L есть единичная окружность, то оператор Шварца совпадает с известным интегралом Шварца; если 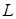 - действительная ось, оператор Шварца есть удвоенный интеграл типа Коши. Для произвольного контура можно дать явное выражение оператора Шварца через функцию Грина. Пусть

 

 

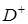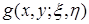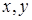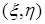-   функция Грина оператора Лапласа для области , причем , a  - гармоническая функция обеих пар переменных  и , принимающая значение , когда одна из точек ,  оказывается лежащей на контуре.

Будем рассматривать  как функцию двух комплексных переменных , , 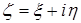изменяющихся каждая в области 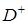, и обозначать ее далее .

Из теории гармонических функций известно (см. [1]), что решение первой краевой задачи гармонических функций - задачи Дирихле - дается формулой

 

 (3.2)

 

где  - комплексная координата точки контура,  - внутренняя нормаль.

Пусть - гармоническая функция, сопряженная функции  по переменной . Она определяется на основании уравнений Коши - Римана формулой

 

 (3.3)

 

где z₀ - фиксированная точка области .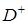

Так как область 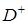 односвязная, то функция  определяется однозначно, причем на основании формулы (3.3) удовлетворяет условию

 

 

Функция

 

 

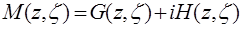
называется комплексной функцией Грина области 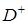. Она будет аналитической по переменной  всюду, кроме точки 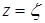, где она имеет логарифмическую особенность.

В силу равенств (3.2) и (3.3) формула

 

 

дает гармоническую функцию , сопряженную функции .

Отсюда равенство

 

 

определяет аналитическую функцию, действительная часть которой на контуре равна заданной функции 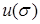, удовлетворяющую дополнительному условию .

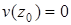Следовательно, оператор Шварца задается формулой

 

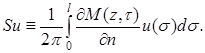 (3.4)

 

Если отбросить условие 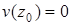, то

 

 (3.5)

 

где  - произвольная постоянная, равная .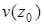

Функция  называется ядром Шварца для контура 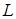. При конформном отображении области  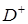на единичный круг она переходит в ядро Шварца для круга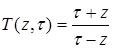

Комплексная функция Грина и оператор Шварца тесно связаны с конформным отображением области на круг. Пусть

 

 

есть функция, конформно отображающая область 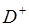 плоскости , ограниченную контуром , на единичный круг плоскости  и переводящая некоторую точку  области в начало координат. В силу взаимной однозначности отображения никакая другая точка области не переходит в начало, поэтому .

Определение аналитической функции, имеющей полюс, по значениям ее действительной части на контуре (задача А).

В предыдущем пункте определялась аналитическая в области функция  по действительной части на контуре. В дальнейшем нам понадобится решение более общей задачи, когда для искомой аналитической функции в некоторой точке области допустим полюс. Задачу эту в дальнейшем, следуя [6], будем именовать задачей А. Дадим ее точную формулировку.

Дан простой гладкий замкнутый контур , ограничивающий внутреннюю область 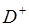. Требуется определить функцию 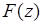, аналитическую в области 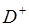, за исключением точки z₀, где для нее допустим полюс порядка не выше  и действительная часть которой на контуре L обращается в заданную функцию .

Соответствующую однородную задачу ( ) назовем задачей А₀. Решение ее будем обозначать .

Дадим сначала решение задачи А₀ для случая, когда контур L есть единичная окружность и .

Выпишем разложение искомой функции в окрестности начала координат:

 

 

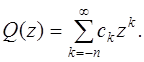
По условию

 

 

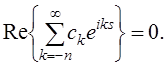
Обозначая , получим

 

 

В силу единственности разложения в ряд Фурье будем иметь

 

 

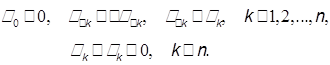
Отсюда

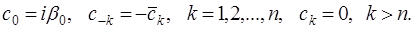
Следовательно, искомая функция Q(z) имеет вид

 

  (3.6)

 

Замечание. 3.1. Если в формулировке задачи А₀ для единичного круга заменить область , внутреннюю для единичной окружности, на область , внешнюю для нее, то как рассуждения, так и окончательный результат останутся неизменными и, следовательно, формула (3.6) дает решение задачи А₀ также и для области 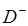, внешней по отношению к единичной окружности с полюсом на бесконечности.

Решение задачи А₀ для произвольной области, а также для единичного круга, но с полюсом в точке , может быть получено из найденного решения при помощи конформного отображения. Пусть

 

 (3.7)

 

есть функция, конформно отображающая область  плоскости  на единичный круг плоскости  так, что некоторая точка  переходит в начало координат  и .

Тогда формула

 

  (3.8)

 

дает решение задачи А₀ для произвольной области  с полюсом порядка  в точке

Теперь мы готовы к тому, чтобы решить задачу А.

По определению оператора Шварца, 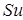 есть аналитическая в области D⁺ функция, действительная часть которой на контуре равна 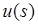. Разность  будет, очевидно, функцией, удовлетворяющей условиям задачи А₀. Следовательно,

 

 

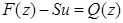
откуда

 

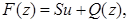 (3.9)

 

где оператор Шварца  определяется формулой (3.4), а решение  однородной задачи А₀ - формулой (3.8).

Как показывают формулы (3.8), (3.9), в решения задач А₀ и А входят линейно  произвольных действительных постоянных

 

Для построения обладающей перечисленными выше свойствами функции по предельным значениям на контуре ее мнимой части  достаточно заметить, что

 

 

откуда

 

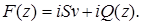 (3.10)

⇐ Предыдущая1234Следующая ⇒

Поделиться: