Лабораторная работа №7. Простая нелинейная регрессия

⇐ ПредыдущаяСтр 9 из 9

Анализируя диаграммы рассеяния двумерной совокупности данных, можно выявить три различных типа взаимосвязей между переменными X и Y. 1. Линейная взаимосвязь. 2. Отсутствие взаимосвязи. 3. Нелинейная взаимосвязь. Линейная взаимосвязь играет такую же важную роль для двумерных данных, как и нормальное распределение для одномерных данных. Прежде всего, линейную зависимость между переменными X и Y легче анализировать. На диаграмме рассеяния точки случайным образом могут концентрироваться вокруг прямой линии, или быть достаточно широко разбросаны, образуя некоторое облако. Набор данных линейной взаимосвязи не должен содержать сильных выбросов. Отсутствие взаимосвязи представляет собой особый случай линейной взаимосвязи, когда соответствующая диаграмма рассеяния имеет совершенно случайный характер, т. е. продвигаясь по ней слева направо, мы не обнаруживаем тенденции направленности вверх (увеличение) или вниз (уменьшение). Такая диаграмма имеет вид либо круглого, либо овального облака. Овал может иметь вертикальную или горизонтальную ориентацию, но без наклона. Фактически, если совокупность данных характеризуется отсутствием взаимосвязи, то, изменяя шкалу той или другой переменной, можно добиться того, что диаграмма рассеяния будет иметь круговую или овальную форму разброса точек. Нелинейная взаимосвязь характеризуется тем, что в двумерной совокупности данных точки на диаграмме рассеяния группируются вокруг некоторой кривой линии. Поскольку разновидностей кривых может быть чрезвычайно много, анализ нелинейной взаимосвязи существенно сложнее, чем линейной. Для переменных X и Y с нелинейной зависимостью корреляционный и регрессионный анализ следует использовать с осторожностью. В некоторых задачах бывает полезно преобразовать одну или обе переменные таким образом, чтобы получить между ними линейную взаимосвязь. Это позволяет упростить анализ (применив корреляцию и регрессию к линейной взаимосвязи), а полученные результаты, если удается, преобразовывают обратно в исходную форму. Важным шагом при выборе нелинейной формы зависимости является изучение графика. Ниже на рисунке изображены четыре выпуклые нелинейные кривые, которые могут быть получены на графике. Метка для каждой кривой обозначает направление выпуклости.

Направление выпуклости соответствует определенному виду функции регрессии.

Так, для данных, имеющих выпуклость в сторону северо-запада (СЗ), используются степенные (при x> 1) и логарифмические функции; для данных, имеющих выпуклость в сторону юго-запада (ЮЗ), используются степенные, логарифмические или экспоненциальные функции; данным с выпуклостью в сторону юго-востока (ЮВ) соответствуют степенные (при x> 1) и экспоненциальные функции.

Кроме того, все четыре кривые данных могут быть смоделированы квадратичной функцией (полиномом второй степени).

Если вид данных на графике не подходит к указанным выше примерам, то следует использовать какую-либо другую форму зависимости.

Например, если данные имеют две выпуклости (S-форма), то можно применить кубическую функцию (полином третьей степени).

В данной лабораторной работе рассмотрим четыре модели нелинейной зависимости между двумя переменными X и Y: полиномиальную, логарифмическую, степенную и экспоненциальную.

В качестве примера используем данные о ценах объектов недвижимости (см. лабораторную работу №5, таблицу 1).

Зависимой переменной Y является стоимость в тысячах долларов, а независимой переменной X – площадь в квадратных метрах.

Из проведенного в лабораторной работе №6 линейного регрессионного анализа для указанных данных получены график линейной функции регрессии и график остатков.

На графике остатков видно, что первые два объекта недвижимости с небольшой площадью и последние несколько объектов с большой площадью имеют отрицательныеостатки.

Это наблюдение показывает, что нелинейное приближение может дать лучшие результаты.

При внимательном рассмотрении диаграммы рассеяния (см. лабораторную работу №5, задание 1) можно заметить, что график функции регрессии имеет небольшую выпуклость в сторону СЗ, хотя кривизна небольшая.

Следовательно, для анализа можно использовать квадратичную, степенную или логарифмическую функции.

Полиномиальное приближение

Рассмотрим квадратичную модель, в которой функция регрессии представляет собой полином второй степени. Уравнение регрессии квадратичной модели имеет следующий вид.

В качестве независимых переменных в уравнении используются переменные x и x².

Построить график квадратичной функции регрессии, отражающей зависимость между стоимостью и площадью жилого объекта.

1. Откройте программу Excel. 2. Щелкните на кнопке Сохранить на панели инструментов Стандартная. 3. В появившемся диалоговом окне откройте папку Статистика и 4. задайте имя файлу Нелинейная регрессия.xls. 5. Откройте файл Двумерные данные.xls. 6. Выделите Лист1 и выполните команду Правка→ Переместить/скопировать лист… 7. В диалоговом окне из списка в книгу: выберите файл Нелинейная регрессия.xls, 8. в списке перед листом: выберите Лист1, 9. установите флажок Создавать копию и 10. щелкните на кнопке ОК. 11. В файле Нелинейная регрессия.xls удалите Лист1, 12. а имя Лист1(2) замените на имя Лист1. 13. Закройте файл Двумерные данные.xls. 14. На диаграмме рассеяния щелкните правой кнопкой мыши на любой точке данных (Ряд1) и в контекстном меню выберите команду Добавить линию тренда… 15. Появится диалоговое окно (см. рисунок ниже).

16. В диалоговом окне на вкладке Тип щелкните по пиктограмме Полиномиальная. Параметр Степень: должен соответствовать числу 2. 17. Откройте вкладку Параметры и 18. в области Название аппроксимирующей (сглаженной) кривой выберите опцию автоматическое:. 19. Убедитесь, что опция пересечение кривой с осью Y в точке: не отмечена. 20. Включите опции показывать уравнение на диаграмме и 21. поместить на диаграмму величину достоверности аппроксимации (R^2). 22. Щелкните на кнопке ОК. 23. Выделите текст с уравнением регрессии и значением R², щелкните у его границы и расположите под заголовком диаграммы. Результат приближения квадратичной функцией немного лучше, чем при линейном приближении, т.к. коэффициент детерминации R², равный 68%, получился больше 66%. Для более точного анализа квадратичной модели получим дополнительные характеристики регрессии, используя инструмент анализа Регрессия. 24. Скопируйте данные с Листа1 (диапазон A1: B16) на Лист2 в такой же диапазон. 25. Выделите столбец B и 26. из контекстного меню выберите команду Добавить ячейки. 27. В ячейку B1 введите метку Площадь^2. 28. Увеличьте ширину столбца B, дважды щелкнув на правой границе его заголовка. 29. Выделите ячейку B2 и введите в нее формулу =A2^2. 30. Скопируйте формулу в остальные ячейки столбца B, выделив ячейку B2 и 31. дважды щелкнув по маркеру заполнения. 32. Выберите команду: Сервис®Анализ данных®Регрессия. 33. В диалоговом окне Регрессия установите параметры как указано ниже на рисунке. 34. Щелкните на кнопке ОК.

35. Выделите диапазон столбцов E: M и увеличьте ширину столбцов, 36. дважды щелкнув по правой границе в строке заголовков столбцов. 37. Удалите часть результатов, относящихся к дисперсионному анализу. 38. Для этого выделите диапазон E10: M14 и 39. выберите из контекстного меню команду Удалить… 40. В диалоговом окне установите опцию ячейки, со сдвигом вверх. 41. Щелкните на кнопке ОК.

Интерпретация результатов

Полученное уравнение с квадратичной функцией регрессии, имеет вид:

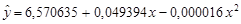. В линейной модели (см. лабораторную работу №6) мы получили стандартную ошибку и нормированный коэффициент детерминации равными $3238 и 0, 6377 соответственно. По сравнению с линейной моделью данная квадратичная модель имеет немного большую стандартную ошибку ($3266) и меньшее значение нормированного коэффициента детерминации (0, 6315). Исходя из этого, можно сказать, что квадратичная модель не является лучше линейной.

В квадратичной модели выполните прогнозирование средней цены для объекта с жилой площадью в 1000 квадратных метров.

1. На Листе2 выделите ячейку A20 и введите в нее значение площади, равное 1000. 2. В ячейку B20 введите формулу = A20^2. 3. В ячейку С20 введите формулу для предсказанной цены = F12 + F13* A20 + F14*B20. 4. Сравните полученную цену с предсказанной ценой в линейной модели. Логарифмическое приближение В логарифмической модели уравнение регрессии имеет следующий вид.

. В качестве независимой переменной в уравнении используется

. Так как при построении линии тренда Excel проводит логарифмирование, то значения переменной X должны быть положительными. Если же среди значений переменной X имеются нулевые или отрицательные значения, то в диалоговом окне Линия тренда на вкладке Тип пиктограмма Логарифмическая будет выделена серым цветом.

Построить график логарифмической функции регрессии, отражающей зависимость между стоимостью и площадью жилого объекта.

1. С Листа1 скопируйте данные вместе с диаграммой на Лист3. 2. Щелкните правой кнопкой мыши на линии тренда и в контекстном меню выберите команду Очистить. 3. На диаграмме рассеяния щелкните правой кнопкой мыши на любой точке данных (Ряд1) и в контекстном меню выберите команду Добавить линию тренда… 4. В диалоговом окне на вкладке Тип щелкните по пиктограмме Логарифмическая. 5. Откройте вкладку Параметры и в области Название аппроксимирующей (сглаженной) кривой выберите опцию автоматическое:. Включите опции показывать уравнение на диаграмме и поместить на диаграмму величину достоверности аппроксимации (R^2). Щелкните на кнопке ОК. 6. Текст с уравнением регрессии и значением R² расположите под заголовком диаграммы. Далее с помощью инструмента анализа Регрессия получим более полные оценки регрессии логарифмической модели. 7. Вставьте в книгу Лист4 и скопируйте в него данные с Листа1 (диапазон A1: B16) в такой же диапазон. 8. Выделите столбец B и из контекстного меню выберите команду Добавить ячейки. 9. В ячейку B1 введите метку Ln(Площадь). Увеличьте ширину столбца B, дважды щелкнув на правой границе его заголовка. 10. Выделите ячейку B2 и введите в нее формулу =LN(A2). В остальные ячейки столбца B скопируйте формулу, выделив ячейку B2 и дважды щелкнув по маркеру заполнения. 11. Выберите команду: Сервис®Анализ данных®Регрессия. В диалоговом окне Регрессия установите следующие параметры. Ü Входной интервал Y: укажите диапазон значений зависимой переменной (C1: C16), включая метку в первой строке. Ü Входной интервал X: укажите диапазон значений независимой переменной (B1: B16), включая метку в первой строке. Ü Метки: включите эту опцию, так как во Входные интервалы X и Y были включены подписи. Ü Параметры вывода: включите Выходной интервал, выберите текстовую строку и введите в нее ссылку на ячейку E1, указывающую левый верхний угол области вывода результатов. Щелкните на кнопке ОК. 12. Выделите диапазон столбцов E: M и увеличьте ширину столбцов, дважды щелкнув по правой границе в строке заголовков столбцов. 13. Удалите часть результатов, относящихся к дисперсионному анализу. Для этого выделите диапазон E10: M14 и выберите из контекстного меню команду Удалить… В диалоговом окне установите опцию ячейки, со сдвигом вверх. Щелкните на кнопке ОК.

Интерпретация результатов

Полученное уравнение с логарифмической функцией регрессии, имеет вид:

. По сравнению с линейной моделью данная логарифмическая модель имеет меньшую стандартную ошибку ($3108< 3238) и большее значение нормированного коэффициента детерминации (0, 6662> 0, 6377). Следовательно, логарифмическая модель является несколько лучше линейной.

В логарифмической модели выполните прогнозирование средней цены для объекта с жилой площадью в 1000 квадратных метров.

1. На Листе4 выделите ячейку A20 и введите в нее значение площади, равное 1000. 2. В ячейку B20 введите формулу = LN(A20). 3. В ячейку С20 введите формулу для предсказанной цены = F12 + F13*B20. 4. Сравните полученную цену с предсказанной ценой в линейной модели. Степенное приближение В степенной модели уравнение регрессии имеет следующий вид.

. При построении линии тренда Excel сначала преобразует степенную модель в линейную. Для этого проводится логарифмирование обеих частей уравнения:

. Затем применяется обычная линейная регрессия для зависимой переменной

и независимой переменной

. В результате Excel определит коэффициент регрессии, соответствующий коэффициенту b степенной модели, и постоянный член

. Чтобы получить уравнение регрессии степенной модели, необходимо определить коэффициент a. Для этого выполняется обратное преобразование, т.е. коэффициент a вычисляется по формуле:

. Поскольку Excel выполняет логарифмическое преобразование исходных данных X и Y, то, как зависимая переменная Y, так и независимая переменная X должны быть положительными. Если какое-либо из значений X или Y равно нулю или отрицательно, то в диалоговом окне Линия тренда на вкладке Тип пиктограмма Степенная будет выделена серым цветом.

Построить график степенной функции регрессии, отражающей зависимость между стоимостью и площадью жилого объекта.

1. Добавьте Лист5. С Листа1 скопируйте данные вместе с диаграммой на Лист5. 2. Щелкните правой кнопкой мыши на линии тренда и в контекстном меню выберите команду Очистить. 3. На диаграмме рассеяния щелкните правой кнопкой мыши на любой точке данных (Ряд1) и в контекстном меню выберите команду Добавить линию тренда… 4. В диалоговом окне на вкладке Тип щелкните по пиктограмме Степенная. 5. Откройте вкладку Параметры и в области Название аппроксимирующей (сглаженной) кривой выберите опцию автоматическое:. Включите опции показывать уравнение на диаграмме и поместить на диаграмму величину достоверности аппроксимации (R^2). Щелкните на кнопке ОК. 6. Текст с уравнением регрессии и значением R² расположите под заголовком диаграммы. Далее с помощью инструмента анализа Регрессия получим более полные оценки регрессии степенной модели. 7. Вставьте в книгу Лист6 и скопируйте в него данные с Листа1 (диапазон A1: B16) в такой же диапазон. 8. В ячейку C1 введите метку Ln(Площадь), а в ячейку D1 введите метку Ln(Цена). Измените ширину столбцов C и D, дважды щелкнув на правой границе в строке заголовков столбцов. 9. Выделите ячейку C2 и введите в нее формулу =LN(A2). 10. Выделите ячейку D2 и введите в нее формулу =LN(B2). 11. Скопируйте формулы в остальные ячейки. Для этого выделите ячейки C2 и D2 и дважды щелкнув по маркеру заполнения ячейки D2. 12. Выберите команду: Сервис®Анализ данных®Регрессия. В диалоговом окне Регрессия установите следующие параметры. Ü Входной интервал Y: укажите диапазон значений зависимой переменной (D1: D16), включая метку в первой строке. Ü Входной интервал X: укажите диапазон значений независимой переменной (C1: C16), включая метку в первой строке. Ü Метки: включите эту опцию, так как во Входные интервалы X и Y были включены подписи. Ü Параметры вывода: включите Выходной интервал, выберите текстовую строку и введите в нее ссылку на ячейку F1, указывающую левый верхний угол области вывода результатов. Щелкните на кнопке ОК. 13. Выделите диапазон столбцов F: N и увеличьте ширину столбцов, дважды щелкнув по правой границе в строке заголовков столбцов. 14. Удалите часть результатов, относящихся к дисперсионному анализу. Для этого выделите диапазон F10: N14 и выберите из контекстного меню команду Удалить… В диалоговом окне установите опцию ячейки, со сдвигом вверх. Щелкните на кнопке ОК.

Интерпретация результатов

Результаты, полученные с помощью инструмента Регрессия относятся к линейной модели преобразованного уравнения регрессии, в котором зависимой переменной является

, а независимой –

. Эти результаты нельзя сравнивать с линейной моделью, рассмотренной в лабораторной работе №6, так как стандартная ошибка в этом случае определяется в единицах измерения

, а значение нормированного коэффициента детерминации является долей изменений

, выраженной через

. Для получения уравнения степенной модели необходимо вычислить коэффициент a, выполнив обратное преобразование.

На основе результатов, полученных с помощью инструмента анализа Регрессия, вычислите коэффициент a для степенной модели.

1. На Листе6 выделите ячейку G14 и введите формулу =EXP(G12) для вычисления коэффициента a. Укажите, какой вид имеет уравнение регрессии полученной степенной модели.

В степенной модели выполните прогнозирование средней цены для объекта с жилой площадью в 1000 квадратных метров.

1. На Листе6 выделите ячейку A20 и введите в нее значение площади, равное 1000. 2. В ячейку B20 введите формулу для предсказанной цены = G14*A20^G13. 3. Сравните полученную цену с предсказанной ценой в линейной модели

Экспоненциальное приближение В экспоненциальной модели уравнение регрессии имеет следующий вид.

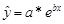. При построении линии тренда Excel сначала преобразует экспоненциальную модель в линейную. Для этого проводится логарифмирование обеих частей уравнения:

. Затем применяется обычная линейная регрессия для зависимой переменной

и независимой переменной х. В результате Excel определит коэффициент регрессии, соответствующий коэффициенту b экспоненциальной модели, и постоянный член

. Чтобы получить уравнение регрессии экспоненциальной модели, необходимо определить коэффициент a. Для этого выполняется обратное преобразование, т.е. коэффициент a вычисляется по формуле:

. Поскольку Excel выполняет логарифмическое преобразование исходных данных Y, то значения зависимой переменная Y должны быть положительными. Если какое-либо из значений Y равно нулю или отрицательно, то в диалоговом окне Линия тренда на вкладке Тип пиктограмма Экспоненциальная будет выделена серым цветом.

Построить график экспоненциальной функции регрессии, отражающей рост продаж компьютеров за период 1987 ¸ 1994 г.г

В таблице 1 представлен временной ряд, определяющий ежегодные продажи компьютеров за период 1987 ¸ 1994 г.г. Таблица 1. Данные продаж за год

Год	Продажи

Построим график временного ряда с использованием Мастера диаграмм.

1. Добавьте Лист7. В ячейку A1 введите метку Год, а в ячейку B1 введите метку Продажи. Из Таблицы 1 в диапазон A2: B9 введите соответствующие данные. 2. Выделите данные о продажах (диапазон B2: B9) и щелкните ра кнопке Мастер диаграмм. 3. В диалоговом окне Мастер диаграмм (шаг 1 из 4): тип диаграммы на вкладке Стандартные в области Тип: выберите График, а в области Вид выберите График с маркерами, помечающими точки данных. Щелкните на кнопке Далее. 4. В диалоговом окне Мастер диаграмм (шаг 2 из 4): источник данных диаграммы на вкладке Ряд щелкните в текстовой строке Подписи оси X: и выберите диапазон A2: A9. Щелкните на кнопке Далее. 5. В диалоговом окне Мастер диаграмм (шаг 3 из 4): параметры диаграммы откройте вкладку Заголовки. В текстовой строке Название диаграммы: введите Ежегодные продажи компьютеров (график). В строке Ось X (категорий): введите Год (от 1 до 8 для линии тренда). В строке Ось Y (значений): введите Единицы продаж. Откройте вкладку Легенда и снимите флажок Добавить легенду. Щелкните на кнопке Далее. 6. В диалоговом окне Мастер диаграмм (шаг 4 из 4): размещение диаграммы включите опцию имеющемся: и щелкните на кнопке Готово. Разместите диаграмму в области D1: L25. 7. Щелкните правой кнопкой мыши на любой точке данных (Ряд1) и в контекстном меню выберите команду Добавить линию тренда… 8. В диалоговом окне на вкладке Тип щелкните по пиктограмме Экспоненциальная. Откройте вкладку Параметры и включите опции показывать уравнение на диаграмме и поместить на диаграмму величину достоверности аппроксимации (R^2). Щелкните на кнопке ОК. 9. Щелкните правой кнопкой мыши по линии тренда и в контекстном меню выберите команду Формат линии тренда… В диалоговом окне на вкладке Вид выберите цвет: линии зеленый. Щелкните на кнопке ОК. 10. Щелкните в выведенном на диаграмму тексте справа от уравнения регрессии, нажмите сначала на клавишу [Delete], а затем три-четыре раза на клавишу пробела. Текст с уравнением и значением R² расположится в одну строку. Переместите текст под заголовок диаграммы. Замечание. Так как для приближения экспоненциальной функцией строится график, а не точечная диаграмма рассеяния, то Excel данные о годе использует как подписи оси X, а роль значений x при построении экспоненциальной линии тренда выполняют числа от 1 до 8. Далее с помощью инструмента анализа Регрессия получим более полные оценки регрессии экспоненциальной модели. 11. Вставьте в книгу Лист8 и скопируйте в него данные с Листа7 (диапазон A1: B9) в такой же диапазон. 12. Выделите столбец B и из контекстного меню выберите команду Добавить ячейки. 13. В ячейку B1 введите метку Х, а в ячейки диапазона B2: B9 введите целые числа от 1 до 8. Уменьшите ширину столбца B, дважды щелкнув на правой границе заголовка. 14. В ячейку D1 введите метку Ln(Продажи). Измените ширину столбца D, дважды щелкнув на правой границе заголовка. 15. Выделите ячейку D2 и введите в нее формулу =LN(C2). 16. Скопируйте формулу в остальные ячейки столбца, дважды щелкну по маркеру заполнения ячейки D2. 17. Выберите команду: Сервис®Анализ данных®Регрессия. В диалоговом окне Регрессия установите следующие параметры. Ü Входной интервал Y: укажите диапазон значений зависимой переменной (D1: D9), включая метку в первой строке. Ü Входной интервал X: укажите диапазон значений независимой переменной (B1: B9), включая метку в первой строке. Ü Метки: включите эту опцию, так как во Входные интервалы X и Y были включены подписи. Ü Параметры вывода: включите Выходной интервал, выберите текстовую строку и введите в нее ссылку на ячейку F1, указывающую левый верхний угол области вывода результатов. Щелкните на кнопке ОК. 18. Выделите диапазон столбцов F: N и увеличьте ширину столбцов, дважды щелкнув по правой границе в строке заголовков столбцов. 19. Удалите часть результатов, относящихся к дисперсионному анализу. Для этого выделите диапазон F10: N14 и выберите из контекстного меню команду Удалить… В диалоговом окне установите опцию ячейки, со сдвигом вверх. Щелкните на кнопке ОК.

Интерпретация результатов

, а независимой – х. Эти результаты нельзя сравнивать с линейной моделью, рассмотренной в лабораторной работе №6, так как стандартная ошибка в этом случае определяется в единицах измерения

, а значение нормированного коэффициента детерминации является долей изменений

. Для получения уравнения экспоненциальной модели необходимо вычислить коэффициент a, выполнив обратное преобразование.

На основе результатов, полученных с помощью инструмента анализа Регрессия, вычислите коэффициент a для экспоненциальной модели.

1. На Листе8 выделите ячейку G14 и введите формулу =EXP(G12) для вычисления коэффициента a. Укажите, какой вид имеет уравнение регрессии полученной экспоненциальной модели.

В экспоненциальной модели выполните прогнозирование средних продаж компьютеров в 1995 г.

1. На Листе8 выделите ячейку A20 и введите год 1995. 2. В ячейку B20 введите значение x, равное 9. 3. В ячейку C20 введите формулу для предсказанной цены = G14*EXP(G13*B20). 4. Какую величину средней продажи компьютеров можно ожидать в 1995 году?

Контрольные вопросы

22. Какие типы взаимосвязей существуют между переменными X и Y? Как можно определить взаимосвязь по диаграмме рассеяния?

23. Как определяется форма нелинейной взаимосвязи с помощью графика?

24. Какие характеристики используются при сравнении нелинейной регрессионной модели с линейной регрессией?

25. Как по найденной регрессионной модели осуществляется прогнозирование переменной Y?

26. Какой вид имеет квадратичная модель регрессии? Какие переменные в уравнении используются в качестве независимых?

27. Какой вид имеет логарифмическая модель регрессии? Какая переменная в уравнении регрессии является независимой? Какое ограничение имеют значения переменной X в логарифмической модели?

28. Какой вид имеет степенная модель регрессии? С какой целью в Excel проводится логарифмическое преобразование уравнения регрессии? Что такое обратное преобразование?

29. Какой вид имеет экспоненциальная модель регрессии? Как определяются коэффициенты a и b уравнения регрессии?

⇐ Предыдущая 1 2 3 4 5 6 7 89