МЕТОД НАИМЕНЬШИХ КВАДРАТОВ ДЛЯ ПРЯМОЙ ЛИНИИ
При обработке наблюдений широко применяется метод наименьших квадратов (МНК). Его суть изложим на частном примере прямой линии.
Пусть на плоскости хоу дано n точек: (х1; у1), (х2; у2), …, ( xn; yn ).
Среди всех прямых линий у=ах+b на плоскости мы ищем наиболее близкую к данной системе точек, причем близость измеряем суммой S квадратов отклонений:
 , (25) , (25)
где  - отклонение вдоль оси y i–той точки от прямой [δ 1> 0, если точка (x1; y1) лежит над прямой ], S – сумма квадратов указанных отклонений по всем n точкам. - отклонение вдоль оси y i–той точки от прямой [δ 1> 0, если точка (x1; y1) лежит над прямой ], S – сумма квадратов указанных отклонений по всем n точкам.
Из всех прямых наилучшей в смысле метода наименьших квадратов будет такая прамая  , для которой сумма S минимальна. , для которой сумма S минимальна.
Если приравнять нулю производные  и и  , то получим систему двух линейных по а и b уравнений, из которых в конечном счете можно найти решение: , то получим систему двух линейных по а и b уравнений, из которых в конечном счете можно найти решение:
 (26) (26)
 (27) (27)
где  и и 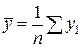 - среднее арифметическое, знак - среднее арифметическое, знак  означает означает  - суммирование по всем точкам. - суммирование по всем точкам.
 . .
Как видим, для углового коэффициента  МНК - прямой в (26) даны три эквивалентных формулы. МНК - прямой в (26) даны три эквивалентных формулы.
Подставив из (27) выражение для  в формулу в формулу  , получим уравнение МНК-прямой , получим уравнение МНК-прямой
 (28) (28)
откуда видно, что  , т.е. эта прямая всегда проходит через точку ( , т.е. эта прямая всегда проходит через точку (  ), являющуюся центром тяжести данной системы точек. ), являющуюся центром тяжести данной системы точек.
Пример 32. Для данных в таблице 13 пяти точек найти МНК - прямую и сумму  квадратов отклонений от нее. квадратов отклонений от нее.
Таблица 13
Обработка данных для нахождения МНК-прямой
| N точки
| x1
| y1
| Δ x1
| y1Δ x1
| (Δ x1)2
| f(x1)
| 
| 
| |
|
| 2, 5
| -1, 8
| -4, 4
| 3, 24
| 2, 45
| 0, 05
| 0, 0025
| |
|
| 2, 2
| -0, 8
| -1, 76
| 0, 64
| 2, 0
| 0, 2
| 0, 04
| |
|
|
| 1, 2
| 1, 2
| 1, 44
| 1, 1
| -0, 1
| 0, 01
| |
|
| 0, 7
| 2, 2
| 1, 54
| 4, 84.
| 0, 65
| 0, 05
| 0, 0025
| |
|
| 1, 8
| 1, 8
| -1, 44
| 0, 64
| 2, 0
| -0, 2
| 0.04
| 
|
| 8, 2
|
| -4, 86
| 10, 8
| -
|
| 0, 095
|
n=5;  ; ;  ; ;
 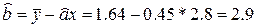
МНК – прямая  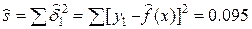
Для контроля полезны суммы:  и и  . .
Метод наименьших квадратов применим не только к прямой, но и к широкому классу функций не только на плоскости, но и в пространстве. Как и во всей статистике, здесь важна интерпретация (истолкование) полученных результатов. Это возможно лишь в рамках принятой вероятностной модели. Поэтому нужно описать принимаемую модель. Например, если мы принимаем, что обрабатываемые точки для системы двух нормальных сл.величин {X, Y) (т.e. [x1; y1 ) - реализации двумерной нормальной сл.величины (X; Y)), то полученная МНК - прямая будет оценкой регрессии Y на Х, а ее угловой коэффициент  выражается через отношение стандартных отклонений и выборочный коэффициент корреляции выражается через отношение стандартных отклонений и выборочный коэффициент корреляции  где sx2 и sy2 - выборочные дисперсии для X и Y. где sx2 и sy2 - выборочные дисперсии для X и Y.
| №п/п
| Новые понятия
| Содержание
| |
|
|
| |
| Статистика
| наука о сборе, классификации, обработке и анализе возможных количественных и качественных данных, о получении из фактов обобщающих выводов
| |
| Генеральная совокупность
| все интересующее нас множество объектов, а также совокупность значений признака присущего объектам
| |
| Метод сплошных наблюдений
| метод, предполагающий измерение всех элементов генеральной совокупности
| |
| Выборочный метод
| метод статистики, основанный на том, что из генеральной совокупности случайно отбирают часть элементов
| |
| Выборка
| совокупность случайно отобранных из всей обследуемой генеральной совокупности элементов х1, x2,....xn„, где n - число выбранных элементов, х1 - значение исследуемого признака у i-го элемента (i = 1, ....n)
| |
| Объем выборки
| число выбранных элементов генеральной совокупности
| |
| Представительная (репрезентативная) выборка
| выборка, хорошо представляющая вероятностные характеристики генеральной совокупности
| |
| Простой случайный отбор
| отбор выборки n элементов непосредственно из всей генеральной совокупности N элементов
| |
| Типический (или расслоенный) случайный отбор
| отбор, при котором объекты отбираются не прямо из всей генеральной совокупности, а из ее определенных частей (слоев)
| |
| Псевдослучайные числа
| числа, генерируемые случайным образом
| |
| Вариационный ряд
| упорядоченная выборка, записанная в порядке возрастания чисел: x(1)≤ x(2)≤ …≤ x(n)
| | |
| Размах вариационного ряда
| расстояние между крайними членами этого ряда: х(n) — x(1)
| | |
| Коэффициент корреляции системы (X, Y): (х1, у1 )....(xn, yn)
двух случайных величин Х и Y:
| Ρ xy=M{(X- μ x)(Y-μ y)}/ (σ xσ y), где
μ ч, μ н - средние значения Х и Y,
σ ч, σ н - средние квадратичные отклонения Х и Y
| | |
| Эмпирическая функция распределения F(x)
| отношение числа точек выборки, лежащих левее точки х на оси ОХ к объему выборки n
| | |
| Кумулятивная кривая распределения
| аппроксимация эмпирической функции распределения
| | |
| Гистограмма
| эмпирический аналог плотности вероятности, состоящий из прямоугольников, площадь которых равна частоте повторения события
| | |
| Полигон
| эмпирический аналог плотности вероятности, ординаты которого равны частоте попадания наблюдений в соответствующей интервал, отложенный по оси абсцесс
| | |
| Случайная величина, подчиняющаяся распределению Стьюдента
|  где n – число степенем свободы, а ξ – сл. величина где n – число степенем свободы, а ξ – сл. величина
| | | | | | | |
Таблица значений функции
| | | | 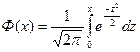 |

| х
| Ф(Х)
| X
| Ф(Х)
| X
| Ф(Х)
| X
| Ф(Х)
| | 0, 00
| 0, 0000
| 0, 32
| 0, 1255
| 0, 64
| 0, 2389
| 0, 96
| 0, 3315
| | 0, 01
| 0, 0040
| 0, 33
| 0, 1293
| 0, 65
| 0, 2422
| 0, 97
| 0, 3340
| | 0, 02
| 0, 0080
| 0, 34
| 0, 1331
| 0, 66
| 0, 2454
| 0, 98
| 0, 3365
| | 0, 03
| 0, 0120
| 0, 35
| 0, 1368
| 0, 67
| 0, 2486
| 0, 99
| 0, 3389
| | 0, 04
| 0, 0160
| 0, 36
| 0, 1406
| 0, 68
| 0, 2517
| 1, 00
| 0, 3413
| | 0, 05
| 0, 0199
| 0, 37
| 0, 1443
| 0, 69
| 0, 2549
| 1, 01
| 0, 3438
| | 0, 06
| 0, 0239
| 0, 38
| 0, 1480
| 0, 70
| 0, 2580
| 1, 02
| 0, 3461
| | 0, 07
| 0, 0279
| 0, 39
| 0, 1517
| 0, 71
| 0, 2611
| 1, 03
| 0, 3485
| | 0, 08
| 0, 0319
| 0, 40
| 0, 1554
| 0, 72
| 0, 2642
| 1, 04
| 0, 3508
| | 0, 09
| 0, 0359
| 0, 41
| 0, 1591
| 0, 73
| 0, 2673
| 1, 05
| 0, 3531
| | 0, 10
| 0, 0398
| 0, 42
| 0, 1628
| 0, 74
| 0, 2703
| 1, 06
| 0, 3554
| | 0, 11
| 0, 0438
| 0, 43
| 0, 1664
| 0, 75
| 0, 2734
| 1, 07
| 0, 3577
| | 0, 12
| 0, 0478
| 0, 44
| 0, 1700
| 0, 76
| 0, 2764
| 1, 08
| 0, 3599
| | 0, 13
| 0, 0517
| 0, 45
| 0, 1736
| 0, 77
| 0, 2794
| 1, 09
| 0, 3621
| | 0, 14
| 0, 0557
| 0, 46
| 0, 1772
| 0, 78
| 0, 2823
| 1, 10
| 0, 3643
| | 0, 15
| 0, 0596
| 0, 47
| 0, 1808
| 0, 79
| 0, 2852
| 1, 11
| 0, 3665
| | 0, 16
| 0, 0636
| 0, 48
| 0, 1844
| 0, 80
| 0, 2881
| 1, 12
| 0, 3686
| | 0, 17
| 0, 0675
| 0, 49
| 0, 1879
| 0, 81
| 0, 2210
| 1, 13
| 0, 3708
| | 0, 18
| 0, 0714
| 0, 50
| 0, 1915
| 0, 82
| 0, 2939
| 1, 14
| 0, 3729
| | 0, 19
| 0, 0753
| 0, 51
| 0, 1950
| 0, 83
| 0, 2967
| 0, 15
| 0, 3749
| | 0, 20
| 0, 0793
| 0, 52
| 0, 1985
| 0, 84
| 0, 2995
| 1, 16
| 0, 3770
| | 0, 21
| 0, 0832
| 0, 53
| 0, 2019
| 0, 85
| 0, 3023
| 1, 17
| 0, 3790
| | 0, 22
| 0, 0871
| 0, 54
| 0, 2054
| 0, 86
| 0, 3051
| 1, 18
| 0, 3810
| | 0, 23
| 0, 0910
| 0, 55
| 0, 2088
| 0, 87
| 0, 3078
| 1, 19
| 0, 3830
| | 0, 24
| 0, 0948
| 0, 56
| 0, 2123
| 0, 88
| 0, 3106
| 1, 20
| 0, 3849
| | 0, 25
| 0, 0987
| 0, 57
| 0, 2157
| 0, 89
| 0, 3133
| 1, 21
| 0, 3869
| | 0, 26
| 0, 1026
| 0, 58
| 0, 2190
| 0, 90
| 0, 3159
| 1, 22
| 0, 3883
| | 0, 27
| 0, 1064
| 0, 59
| 0, 2224
| 0, 91
| 0, 3186
| 1, 23
| 0, 3907
| | 0, 28
| 0, 1103
| 0, 60
| 0, 2257
| 0, 92
| 0, 3212
| 1, 24
| 0, 3925
| | 0, 29
| 0, 1141
| 0, 61
| 0, 2291
| 0, 93
| 0, 3238
| 1, 25
| 0, 3944
| | 0, 30
| 0, 1179
| 0, 62
| 0, 2324
| 0, 94
| 0, 3264
|
|
| | 0, 31
| 0, 1217
| 0, 63
| 0, 2357
| 0, 95
| 0, 3289
|
|
|
| х
| Ф(х)
| X
| Ф(х)
| X
| Ф(х)
| X
| Ф(х)
|
| | 1, 26
| 0, 3962
| 1, 59
| 0, 4441
| 1, 92
| 0, 4726
| 2, 50
| 0, 4938
| | 1, 27
| 0, 3980
| 1, 60
| 0, 4452
| 1, 93
| 0, 4732
| 2, 52
| 0, 4941
| | 1, 28
| 0, 3997
| 1, 61
| 0, 4463
| 1, 94
| 0, 4738
| 2, 54
| 0, 4945
| | 1, 29
| 0, 4015
| 1, 62
| 0, 4474
| 1, 95
| 0, 4744
| 2, 56
| 0, 4849
| | 1, 30
| 0, 4032
| 1, 63
| 0, 4484
| 1, 96
| 0, 4750
| 2, 58
| 0, 4951
| | 1, 31
| 0, 4049
| 1, 64
| 0, 4495
| 1, 97
| 0, 4756
| 2, 60
| 0, 4953
| | 1, 32
| 0, 4066
| 1, 65
| 0, 4505
| 1, 98
| 0, 4761
| 2, 62
| 0, 4956
| | 1, 33
| 0, 4082
| 1, 66
| 0, 5415
| 1, 99
| 0, 4767
| 2, 64
| 0, 4959
| | 1, 34
| 0, 4099
| 1, 67
| 0, 5425
| 2, 00
| 0, 4742
| 2, 66
| 0, 4961
| | 1, 35
| 0, 4115
| 1, 68
| 0, 4535
| 2, 02
| 0, 4783
| 2, 68
| 0, 4963
| | 1, 36
| 0, 4131
| 1, 69
| 0, 4545
| 2, 04
| 0, 4795
| 2, 70
| 0, 4965
| | 1, 37
| 0, 4147
| 1, 70
| 0, 4554
| 2, 06
| 0, 4803
| 2, 72
| 0, 4967
| | 1, 38
| 0, 4162
| 1, 71
| 0, 4564
| 2, 08
| 0, 4812
| 2, 74
| 0, 4969
| | 1, 39
| 0, 4177
| 1, 72
| 0, 4573
| 2, 10
| 0, 4821
| 2, 76
| 0, 4971
| | 1, 40
| 0, 4192
| 1, 73
| 0, 4582
| 2, 12
| 0, 4830
| 2, 78
| 0, 4973
| | 1, 41
| 0, 4207
| 1, 74
| 0, 4591
| 2, 14
| 0, 4838
| 2, 80
| 0, 4974
| | 1, 42
| 0, 4222
| 1, 75
| 0, 4599
| 2, 16
| 0, 4846
| 2, 82
| 0, 4976
| | 1, 43
| 0, 4236
| 1, 76
| 0, 4608
| 2, 18
| 0, 4854
| 2, 84
| 0, 4977
| | 1, 44
| 0, 4251
| 1, 77
| 0, 4616
| 2, 20
| 0, 4861
| 2, 86
| 0, 4979
| | 1, 45
| 0, 4265
| 1, 78
| 0, 4625
| 2, 22
| 0, 4868
| 2, 88
| 0, 4980
| | 1, 46
| 0, 4279
| 1, 79
| 0, 4633
| 2, 24
| 0, 4875
| 2, 90
| 0, 4981
| | 1, 47
| 0, 4292
| 1, 80
| 0, 4641
| 2, 26
| 0, 4881
| 2, 92
| 0, 4982
| | 1, 48
| 0, 4306
| 1, 81
| 0, 4649
| 2, 28
| 0, 4887
| 2, 94
| 0, 4984
| | 1, 49
| 0, 4319
| 1, 82
| 0, 4656
| 2, 30
| 0, 4893
| 2, 96
| 0, 4985
| | 1, 50
| 0, 4332
| 1, 83
| 0, 4664
| 2, 32
| 0, 4898
| 2, 98
| 0, 4986
| | 1, 51
| 0, 4345
| 1, 84
| 0, 4671
| 2, 34
| 0, 4904
| 3, 00
| 0, 49865
|
| | 1, 52
| 0, 4357
| 1, 85
| 0, 4678
| 2, 36
| 0, 4909
| 3, 20
| 0, 49931
|
| | 1, 53
| 0, 4370
| 1, 86
| 0, 4686
| 2, 38
| 0, 4913
| 3, 40
| 0, 49966
|
| | 1, 54
| 0, 4382
| 1, 87
| 0, 4693
| 2, 40
| 0, 4918
| 3, 60
| 0, 499841
| | | 1, 55
| 0, 4394
| 1, 88
| 0, 4699
| 2, 42
| 0, 4922
| 3, 80
| 0, 499928
| | | 1, 56
| 0, 4406
| 1, 89
| 0, 4706
| 2, 44
| 0, 4927
| 4, 00
| 0, 499968
| | | 1, 57
| 0, 4418
| 1, 90
| 0, 4713
| 2, 46
| 0, 4931
| 4, 50
| 0, 499997
| | | 1, 58
| 0, 4429
| 1, 91
| 0, 4719
| 2, 48
| 0, 4934
| 5, 00
| 0, 499997
| | | | | | | | | | | | |
Критические точки распределения х2
| Число степеней свободы k
| Уровень значимости а
| | 0, 01
| 0, 025
| 0, 05
| 0, 95
| 0, 975
| 0, 99
| |
| 6, 6
| 5, 0
| 3, 8
| 0, 0039
| 0, 00098
| 0, 00016
| |
| 9, 2
| 7, 4
| 6, 0
| 0, 103
| 0, 051
| 0, 020
| |
| 11, 3
| 9, 4
| 7, 8
| 0, 352
| 0, 216
| 0, 115
| |
| 13, 3
| 11, 1
| 9, 5
| 0, 711
| 0, 484
| 0, 297
| |
| 15, 1
| 12, 8
| 11, 1
| 1, 15
| 0, 831
| 0, 554
| |
| 16, 8
| 14, 4
| 12, 6
| 1, 64
| 1, 24
| 0, 872
| |
| 18, 5
| 16, 0
| 14, 1
| 2, 17
| 1, 69
| 1, 24
| |
| 20, 1
| 17, 5
| 15, 5
| 2, 73
| 2, 18
| 1, 65
| |
| 21, 7
| 19, 0
| 16, 9
| 3, 33
| 2, 70
| 2, 09
| |
| 23, 3
| 20, 5
| 18, 3
| 3, 94
| 3, 25
| 2, 56
| |
| 24, 7
| 21, 9
| 19, 7
| 4, 57
| 3, 82
| 3, 05
| |
| 26, 2
| 23, 3
| 21, 0
| 5, 23
| 4, 40
| 3, 57
| |
| 27, 7
| 24, 7
| 22, 4
| 5, 89
| 5, 01
| 4, 11
| |
| 29, 1
| 26, 1
| 23, 7
| 6, 57
| 5, 63
| 4, 66
| |
| 30, 6
| 27, 5
| 25, 0
| 7, 26
| 6, 26
| 5, 23
| |
| 32, 0
| 28, 8
| 26, 3
| 7, 96
| 6, 91
| 5, 81
| |
| 33, 4
| 30, 2
| 27, 6
| 8, 67
| 7, 56
| 6, 41
| |
| 34, 8
| 31, 5
| 28, 9
| 9, 39
| 8, 23
| 7, 01
| |
| 36, 2
| 32, 9
| 30, 1
| 10, 1
| 8, 91
| 7, 63
| |
| 37, 6
| 34, 2
| 31, 4
| 10, 9
| 9, 59
| 8, 26
| |
| 38, 9
| 35, 5
| 32, 7
| 11, 6
| 10, 3
| 8, 90
| |
| 40, 3
| 36, 8
| 33, 9
| 12, 3
| 11, 0
| 9, 54
| |
| 41, 6
| 38, 1
| 35, 2
| 13, 1
| 11, 7
| 10, 2
| |
| 43, 0
| 39, 4
| 36, 4
| 13, 8
| 12, 4
| 10, 9
| |
| 44, 3
| 40, 6
| 37, 7
| 14, 6
| 13, 1
| 11, 5
| |
| 45, 6
| 41, 9
| 38, 9
| 15, 4
| 13, 8
| 12, 2
| |
| 47, 0
| 43, 2
| 40, 1
| 16, 2
| 14, 6
| 12, 9
| |
| 48, 3
| 44, 5
| 41, 3
| 16, 9
| 15, 3
| 13, 6
| |
| 49, 6
| 45, 7
| 42, 6
| 17, 7
| 16, 0
| 14, 3
| |
| 50, 9
| 47, 0
| 43, 8
| 18, 5
| 16, 8
| 15, 0
|
Популярное:
|

