
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Методические указания к заданию 1
Фермерское хозяйство, ориентированное на выращивание яровой пшеницы и овса, имеет 80га пашни, 630человеко-дней трудовых ресурсов и 1800 л топлива, которые используются в течение производственногоцикла. Планируется реализовать выращенную продукцию из расчёта 3600 руб. с 1га, засеянного пшеницей, и 2900 руб. с 1 га, засеянного овсом. Технологические коэффициенты потребностей в трудовых ресурсах и в топливе на 1 га в течение всего цикла приведены в табл. 13. Таблица № 13
1. Составить экономико-математическую модель задачи при условии максимизации выручки от реализации культур в конце цикла в виде задачи линейного программирования. 2. Решить поставленную задачу графическим способом. 3. Составить двойственную задачу. 4. Найти решение двойственной задачи по решению прямой задачи. 5. Определить оценку полезности используемых ресурсов и их дефицитность. 6. Определить для каждой культуры, выгодно ли её выращивать. Решение. 1) Определим переменные задачи. Пусть а) Площадь пашни, засеянная культурами, составит Учитывая условие максимизации выручки, получим задачу линейного программирования:
2) Решим задачу полученную задачу линейного программирования графически. а) Найдём область допустимых решений как пересечение решений неравенств системы условий. Решения неравенств и ОДР представим на рис. 2. Решаем первое неравенство:
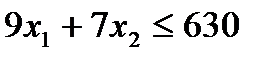 . Граница решения этого неравенства описывается уравнением: . Граница решения этого неравенства описывается уравнением: 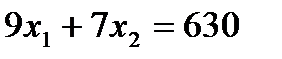 . Это прямая. Обозначим её через . Это прямая. Обозначим её через 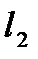 . Построим её также по двум точкам: . Построим её также по двум точкам: 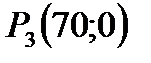 и и 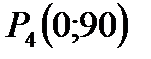 (см. рис. 2). Определим искомую область по контрольной точке. Возьмём точку (см. рис. 2). Определим искомую область по контрольной точке. Возьмём точку 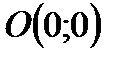 . . 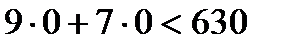 . Решение второго неравенства содержит точку . Решение второго неравенства содержит точку  . .
Решим третье неравенство: Определим искомую область по контрольной точке. Возьмём точку б) Построим линию уровня и градиент. В качестве линии уровня для целевой функции Координаты градиента целевой функции Z равны коэффициентам при переменных в целевой функции: в) Определим решение задачи, передвигая линию уровня в направлении градиента. Решением будет точка Тогда 3) Строим двойственную задачу, используя правила составления двойственной задачи. Учтём, что число переменных двойственной задачи равно трём, а число ограничений двум.
4) Найдём решение двойственной задачи, используя вторую теорему двойственности. Для этого найдём остатки ресурсов при оптимальном плане Проверим условия второй теоремы двойственности: Из проверки этих условий получаем для двойственной задачи:
Получили систему уравнений для вычисления значений 5) Так как
6) Так как посевные площади
Популярное:
|
Последнее изменение этой страницы: 2016-04-09; Просмотров: 711; Нарушение авторского права страницы