Дизъюнктивные и конъюнктивные нормальные формы

Элементарной конъюнкциейназывается конъюнкция переменных высказываний и (или) их отрицаний.

Элементарной дизъюнкциейназывается дизъюнкция переменных высказываний и (или) их отрицаний.

Дизъюнктивной нормальной формой (ДНФ) данной формулы называется равносильная ей формула, представляющая собой дизъюнкцию элементарных конъюнкций.

Конъюнктивной нормальной формой (КНФ) данной формулы называется равносильная ей формула, представляющая собой конъюнкцию элементарных дизъюнкций.

Для того чтобы построить по данной формуле алгебры логики равносильную ей ДНФ или КНФ необходимо выразить все операции через дизъюнкцию, конъюнкцию и отрицание, воспользоваться законом де Моргана для того, чтобы отрицания стояли лишь над элементарными переменными высказываниями, раскрыть скобки (для построения ДНФ) или воспользоваться дистрибутивным законом (для построения КНФ).

Всякая функция алгебры логики может быть представлена в виде формулы, содержащей только операции конъюнкции, дизъюнкции и отрицания.

Элементарная конъюнкция (дизъюнкция) называется правильной, если в нее каждая переменная входит не более одного раза, включая ее вхождение и под знаком отрицания.

Элементарная конъюнкция (дизъюнкция) называется полной относительно переменных x, y, z, если в нее входит каждая из этих переменных не менее одного раза, включая и их вхождение под знаком отрицания.

Совершенной дизъюнктивной нормальной формой (СДНФ) относительно переменных x, y, z, называется дизъюнктивная нормальная форма, в которой нет одинаковых элементарных конъюнкций и все элементарные конъюнкции правильные и полные относительно переменных x, y, z.

Совершенная дизъюнктивная нормальная форма (СДНФ) для булевой функции , не равной тождественно нулю, имеет вид:

где символ определяется следующим образом:

Алгоритм построения СДНФ:

1) построить таблицу истинности данной булевой функции;

2) единичному значению булевой функции будет соответствовать элементарная конъюнкция , где – соответствующий набор значений переменных. В конъюнкции мы записываем , если , и , если . Элементарные конъюнкции соединяются знаком « ».

Совершенной конъюнктивной нормальной формой (СКНФ) относительно переменных x, y, z, называется конъюнктивная нормальная форма, в которой нет одинаковых элементарных дизъюнкций и все элементарные дизъюнкции правильные и полные относительно переменных x, y, z.

Совершенная конъюнктивная нормальная форма (СКНФ) для функции , отличной от тождественной единицы, имеет вид:

Алгоритм построения СКНФ:

1) построить таблицу истинности данной булевой функции;

2) каждому нулевому значению булевой функции будет соответствовать элементарная дизъюнкция , где – соответствующий набор значений переменных. В дизъюнкции мы записываем , если , и , если . Дизъюнкции соединяются знаком « ».

Алгоритмы переходов от одной формы к другой:

а) переход от ДНФ к КНФ: ставим над ДНФ два отрицания и с помощью правил де Моргана (не трогая верхнее отрицание) приводим отрицание ДНФ снова к ДНФ. При этом приходится раскрывать скобки с использованием правила поглощения (или правила Блейка). Отрицание (верхнее) полученной ДНФ (снова по правилу де Моргана) сразу дает нам КНФ:

.

Заметим, что КНФ можно получить и из первоначального выражения, если вынести у за скобки.

б) переход от КНФ к ДНФ: осуществляется простым раскрытием скобок (при этом опять-таки используется правило поглощения):

.

Таким образом, получили ДНФ.

в) переход от ДНФ к СДНФ: если в какой-то простой конъюнкции недостает переменной, например, z, вставляем в нее выражение , после чего раскрываем скобки (при этом повторяющиеся дизъюнктные слагаемые не пишем):

.

г) переход от КНФ к СКНФ осуществляется способом, аналогичным предыдущему: если в простой дизъюнкции не хватает какой-то переменной (например, z, то добавляем в нее выражение (это не меняет самой дизъюнкции), после чего раскрываем скобки с использованием распределительного закона):

Таким образом, из КНФ получена СКНФ.

Заметим, что минимальную или сокращенную КНФ обычно получают из соответствующей ДНФ.

Пример 1. Привести к СКНФформулу (x Ù (y ® z)).

Решение:

x Ù (y ® z) « x Ù (Ø y Ú z) – КНФ,

x Ú (y Ù Ø y) Ù (Ø y Ú z) Ú (x Ù Ø x) « (x Ú y) Ù (x Ú Ø y) Ù (Ø y Ú z Ú x) Ù Ù (Ø yÚ z Ú Ø x) « (x Ú y) Ú (z Ú Ø z) Ù (x Ú Ø y) Ú (z Ú Ø z) Ù (Ø y Ú z Ú x) Ù Ù (Ø y Ú Ú z Ú Ø x) « (x Ú y Ú z) Ù (x Ú y Ú Ø z) Ù (x Ú Ø y Ú z) Ù (x Ú Ø y Ú Ú Ø z) Ù (Ø y Ú z Ú x) Ù (Ø y Ú z Ú Ø x).

Пример 2. Привести к СКНФформулу ((x Ù y) ® (x Ù z)).

Решение:

(x Ù y) ® (x Ù z) « Ø (x Ù y) Ú (x Ù z) « (Ø x Ú Ø y) Ú (x Ù z) « (Ø x Ú Ø y Ú Ú x) Ù (Ø x Ú Ø y Ú z) – КНФ,

(Ø x Ú Ø y Ú x) Ù (Ø x Ú Ø y Ú z) «(Ø x Ú Ø y Ú z).

Пример 3. Привести выражение к ДНФ.

Решение:

Понижаем отрицания по правилу де Моргана. Получаем: .

Пример 4. Построить СДНФ для функции .

Решение:

.

Пример 5. Построить СКНФ для функции .

Решение:

.

Пример 6. Привести формулу к СДНФ с помощью эквивалентных преобразований.

Решение:

– ДНФ.

= =

= Полученная формула – СДНФ.

Пример 7. Привести формулу к СДНФ с помощью эквивалентных преобразований.

Решение:

=

= = =

= = – СДНФ.

Пример 8. С помощью эквивалентных преобразований привести к ДНФ, КНФ, СДНФ, СКНФ функцию f = Ø ((x Ú Ø y) ® (z « Ø x)).

Решение:

Приводим к ДНФ:

Ø ((x Ú Ø y) ® (z « Ø x)) « Ø ((Ø x Ù y) Ú (z « Ø x)) « Ø ((Ø x Ù y) Ú (Ø z Ú Ø x) Ù Ù (x Ú z)) «(x Ú Ø y) Ù ((z Ù x) Ú (Ø x Ù Ø z) « (z Ù x) Ù (x Ú Ø y) Ú (Ø x Ù Ø z) « « (z Ù x Ù x) Ú (z Ù x Ù Ø y) Ú (Ø x Ù Ø z).

Приводим к СДНФ:

(z Ù x Ù x) Ú (z Ù x Ù Ø y) Ú (Ø x Ù Ø z) « (z Ù x) Ú (z Ù x Ù Ø y) Ú (Ø x Ù Ø z) « (zÙ Ù x) Ù (y Ú Ø y) Ú (z Ù x Ù Ø y) Ú (Ø x Ù Ø z) Ù (y Ú Ø y) « (z Ù x Ù y) Ú (z Ù x Ù Ù Ø y)Ú (z Ù x Ù Ø y) Ú (Ø x Ù Ø z Ù y) Ú (Ø x Ù Ø z Ù Ø y).

Переход от ДНФ к КНФ:

Ø (Ø ((z Ù x Ù x) Ú (z Ù x Ù Ø y) Ú (Ø x Ù Ø z))) « Ø ((Ø z Ú Ø x Ú Ø x) Ù (Ø z Ú Ø x Ú Ú y) Ù (x Ú z)) « Ø ((Ø z Ú Ø x) Ù (Ø z Ú Ø x Ú y) Ù (x Ú z)) « Ø (Ø z Ú (Ø x Ù Ø x) Ú Ú (Ø x Ù y) Ù (x Ú z)) « Ø (Ø z Ú (Ø x Ù Ø x) Ú (Ø x Ù y Ù x) Ú (Ø x Ù y Ù z)) « z Ù (xÚ x) Ù (x Ú Ø y Ú Ø x) Ù (x Ú Ø y Ú Ø z).

Приводим к СКНФ:

z Ù (x Ú x) Ù (x Ú Ø y Ú Ø x) Ù (x Ú Ø y Ú Ø z) « z Ú (y Ù Ø y) Ù x Ú (y Ù Ø y) Ù (x Ú Ú Ø y Ú Ø z) « (z Ú y) Ù (z Ú Ø y) Ù (x Ú y) Ù (x Ú Ø y) Ù (x Ú Ø y Ú Ø z) « (z Ú y) Ú Ú (x Ù Ø x) Ù (z Ú Ø y) Ú (x Ù Ø x) Ù (x Ú y) Ú (z Ù Ø z) Ù (x Ú Ø y Ú Ø z) « (z Ú y Ú Ú x) Ù (z Ú y Ú Ø x) Ù (z Ú Ø y Ú x) Ù (z Ú Ø y Ú Ø x) Ù (x Ú y Ú z) Ù (x Ú y Ú Ø z) Ù (xÚ Ø y Ú Ø z) «(z Ú y Ú x) Ù (z Ú y Ú Ø x) Ù (z Ú Ø y Ú x) Ù (z Ú Ø y Ú Ø x) Ù (x Ú yÚ Ú Ø z) Ù (x Ú Ø y Ú Ø z).

Пример 10. Для функции f(x, y, z) = (x ~ z) | ((x y) ~ (y z))

а) составить таблицу истинности;

б) написать для нее СДНФ или СКНФ.

Решение:

а) в таблицу истинности данной функции полезно включить таблицы истинности промежуточных функций:

xyz x ~ z x y y z (x y) ~ (y z) (x~ z)|((x y) ~ (yz)

б) составить СДНФ и СКНФ по полученной таблице. СДНФ составляется по единицам таблицы истинности, причем если f(x, y, z) = 1, то если х = 0, в соответствующей конъюнкции СДНФ берется , а если х = 1 в СДНФ берется х. Аналогично поступают и с другими переменными, поэтому СДНФ для данной функции имеет вид: .

СКНФ составляется по нулям таблицы истинности, если f(x, y, z) = 0 и х = 0, то в соответствующей дизъюнкции берется х, а если х = 1, то . Таким образом, СКНФ для данной функции имеет вид:

.

Заметим, что по определению СДНФ и СКНФ, переменные (в каждой конъюнкции и дизъюнкции соответственно) должны следовать в одинаковом порядке.

Упражнения

1. Построить СДНФ для функций:

a) f(x, y, z)=(x y) (y z);

b) f(x, y)=(xy 1) (x z);

c) f(x, y, z)=xyz (x z) (xyz 1);

d) f(x, y, z)=(xy z) (xz y);

e) f(x, y)=(x y)(z 1);

f) f(x, y)=(x y) (z y);

g) f(x, y)=(x z) xy;

h) f(x, y, z)=(xy z) (xz y);

i) f(x, y, z)=(xy z) (xz y);

j) f(x, y, z)=(x z) (x y) (y z);

k) f(x, y, z)=(x z) (x y).

2. Построить СКНФ для функций:

a) f(x, y, z)=(x y) (y z);

b) f(x, y)=(xy 1) (x z);

c) f(x, y, z)=xyz (x z) (xyz 1);

d) f(x, y, z)=(xy z) (xz y);

e) f(x, y)=(x y)(z 1);

f) f(x, y)=(x y) (z y);

g) f(x, y)=(x y) xz;

h) f(x, y, z)=(xy z) (xz y);

i) f(x, y, z)=(xy z) (xz y);

j) f(x, y, z)=(xz (x y)) (y z);

k) f(x, y, z)=(x z) (x y) (y z).

Индивидуальное задание

6. Привести функцию к ДНФ, затем к СДНФ, с помощью законов алгебры логики:

6.1 ;

6.2 ;

6.3 ;

6.4 ;

6.5 ;

6.6 ;

6.7 ;

6.8 ;

6.9 ;

6.10 ;

6.11 ;

6.12 ;

6.13 ;

6.14 ;

6.15 .

7. Найти по таблице истинности СДНФ и СКНФ:

7.1 ;

7.2 ;

7.3 ;

7.4 ;

7.5 ;

7.6 ;

7.7 ;

7.8 ;

7.9 ;

7.10 ;

7.11 ;

7.12 ;

7.13 ;

7.14 ;

7.15 .

8. От ДНФ перейти к КНФ, затем к СКНФ:

8.1 ;

8.2 ;

8.3 ;

8.4 ;

8.5 ;

8.6 ;

8.7 ;

8.8 ;

8.9 ;

8.10 .

8.11 ;

8.12 ;

8.13 ;

8.14 ;

8.15 .

Сокращенная ДНФ

Любую функцию (кроме тождественного нуля) можно представить в виде СДНФ. На практике часто бывает удобно получить (вместо СДНФ) как можно более “короткую” ДНФ. Словам “короткая ДНФ” можно придать разный смысл, а именно ДНФ называется:

– минимальной, если она содержит наименьшее число букв (среди всех ДНФ ей равносильных);

– кратчайшей, если она содержит минимальное количество знаков дизъюнкции;

– тупиковой, если уничтожение одной или нескольких букв в ней приводит к неравной ДНФ;

– сокращенной ДНФ, если ее упрощение проведено с помощью правила Блейка.

На практике наиболее важной представляется нахождение минимальной ДНФ, но алгоритм ее нахождения по существу является вариантом перебора всех равносильных ДНФ. Проще всего находить сокращенную ДНФ по карте Карно.

Алгоритм получения сокращенной ДНФ по карте Карно:

· составляем таблицу истинности;

· построим таблицу – карту Карно;

· объединяем две рядом стоящие единицы (или 4, 8, 16), наборы (10) и (00) считаются рядом стоящими;

· выписываем строки, соответствующие объединенным единицам одну под другой, к i–му столбцу, в котором повторяются все нули, – переменную , к столбцу, в котором стоят все единицы, – переменную , затем переменные объединить знаком конъюнкции;

· все полученные конъюнкции объединяем знаком дизъюнкции, получится сокращенная ДНФ.

Метод Блейка построения сокращенной ДНФ из произвольной ДНФ:

1 этап. Производится операция обобщенного склеивания по формуле до тех пор, пока это возможно: если среди дизъюнктных слагаемых в ДНФ имеются слагаемые , то ко всей дизъюнкции добавляем слагаемое К₁К_2,проделываем эту операцию несколько раз (можно последовательно, можно одновременно) для всех возможных пар слагаемых, а затем применяем обычное поглощение.

2 этап. Производится операция поглощения . Операции применяются слева направо: если добавляемое слагаемое уже содержалось в ДНФ, то его можно отбросить совсем, например, .

Пример 1. Сократить ДНФ по правилу Блейка:

Пример 2. Сократить функцию по карте Карно:

			f

Составляем карту Карно:

Выписываем строки, соответствующие четырем единицам:

Ко второму столбцу выписываем одну переменную – . К следующим четырем единицам выписываем переменную – .

СДНФ функции содержит (по числу единиц) шесть дизъюнктных слагаемых, но ее сокращенная ДНФ содержит (после объединения единиц) всего две буквы: f = x₁x_2.

Упражнения

1. Сократить функцию по карте Карно:

а)

Ответ: .

с)

Ответ: f(x, y, z) = .

2. Составить карту Карно и найти сокращенную ДНФ для функций:

a) f(x, y)=(xy ;

b) f(x, y)=((x );

c) f(x, y)=(x y) 0;

d) f(x, y)=(x y) ;

e) f(x, y)=(x (x y);

f) f(x, y)=(x (x y))(x y).

Индивидуальное задание

9. Сократить ДНФ по правилу Блейка:

9.1 ;

9.2 ;

9.3 ;

9.4 ;

9.5 ;

9.6 ;

9.7 ;

9.8 ;

9.9 ;

9.10 ;

9.11 ;

9.12 ;

9.13 ;

9.14 ;

9.15 .

10. Составить карту Карно и найти сокращенную ДНФ для функций:

10.1 ;

10.2 ;

10.3 ;

10.4 ;

10.5 ;

10.6 ;

10.7 ;

10.8 ;

10.9 ;

10.10 ;

10.11 ;

10.12 ;

10.13 ;

10.14 ;

10.15 .

11. С помощью карт Карно по данной таблице истинности для функции четырех переменных и найти ее сокращенную ДНФ:

11.1	х₁, х₂		11.2	х₁, х₂	11.7	х₁, х₂	11.3	х₁, х₂
x₃, x₄	0 0	0 1	1 1	1 0		x₃, x₄	0 0	0 1	1 1	1 0	x₃, x₄	0 0	0 1	1 1	1 0	x₃, x₄	0 0	0 1	1 1	1 0
0 0						0 0					0 0					0 0
0 1						0 1					0 1					0 1
1 1						1 1					1 1					1 1
1 0						1 0					1 0					1 0
11.4	х₁, х₂		11.5	х₁, х₂	11.6	х₁, х₂	11.7	х₁, х₂
x₃, x₄	0 0	0 1	1 1	1 0		x₃, x₄	0 0	0 1	1 1	1 0	x₃, x₄	0 0	0 1	1 1	1 0	x₃, x₄	0 0	0 1	1 1	1 0
0 0						0 0					0 0					0 0
0 1						0 1					0 1					0 1
1 1						1 1					1 1					1 1
						1 0					1 0					1 0
11.8	х₁, х₂		11.9	х₁, х₂	11.10	х₁, х₂	11.11	х₁, х₂
x₃, x₄	0 0	0 1	1 1	1 0		x₃, x₄	0 0	0 1	1 1	1 0	x₃, x₄	0 0	0 1	1 1	1 0	x₃, x₄	0 0	0 1	1 1	1 0
0 0						0 0					0 0					0 0
0 1						0 1					0 1					0 1
1 1						1 1					1 1					1 1
						1 0					1 0					1 0
11.12	х₁, х₂		11.13	х₁, х₂	11.14	х₁, х₂	11.15	х₁, х₂
x₃, x₄	0 0	0 1	1 1	1 0		x₃, x₄	0 0	0 1	1 1	1 0	x₃, x₄	0 0	0 1	1 1	1 0	x₃, x₄	0 0	0 1	1 1	1 0
0 0						0 0					0 0					0 0
0 1						0 1					0 1					0 1
1 1						1 1					1 1					1 1
						1 0					1 0					1 0

Логические схемы

Логический элемент компьютера – это часть электронной логической схемы, которая реализует элементарную логическую функцию.

Логическими элементами компьютеров являются электронные схемы И, ИЛИ, НЕ, И–НЕ, ИЛИ–НЕ и другие (называемые также вентилями), а также триггер.

С помощью этих схем можно реализовать любую логическую функцию, описывающую работу устройств компьютера. Обычно у вентилей бывает от двух до восьми входов и один или два выхода.

Работу логических элементов описывают с помощью таблиц истинности.

Переключательная схема – это схематическое изображение некоторого устройства, состоящего из переключателей и соединяющих их проводников, а также из входов и выходов, на которые подается и с которых снимается электрический сигнал.

Каждый переключатель имеет только два состояния: замкнутое и разомкнутое. Переключателю Х поставим в соответствие логическую переменную х, которая принимает значение 1 в том и только в том случае, когда переключатель Х замкнут и схема проводит ток; если же переключатель разомкнут, то х равен нулю.

Всей переключательной схеме также можно поставить в соответствие логическую переменную, равную единице, если схема проводит ток, и равную нулю – если не проводит. Эта переменная является функцией от переменных, соответствующих всем переключателям схемы, и называется функцией проводимости.

При рассмотрении переключательных схем возникают две основные задачи: синтез и анализ схемы.

Синтез схемы сводится к следующим трем этапам:

· составление функции проводимости по таблице истинности, отражающей эти условия;

· упрощение этой функции;

· построение соответствующей схемы.

Анализ схемы сводится к:

· определению значений ее функции проводимости при всех возможных наборах входящих в эту функцию переменных;

· получению упрощенной формулы.

Простейшая схема, содержащая один переключатель P, имеет один вход и один выход :

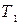
Истинному высказыванию P = «переключатель P замкнут» поставим в соответствие переключатель P. В этом случае схема пропускает ток.

Высказыванию соответствует выражение «переключатель Pразомкнут», схема не проводит ток. Истина («1») интерпретируется как состояние переключателя «ток проходит», «0» (ложь) – «ток не проходит».

Конъюнкциидвух высказываний P& Qсоответствует схема с последовательным соединением контактов:

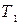
Дизъюнкции двух высказываний P Q соответствует схема с параллельным соединением контактов:

⇐ Предыдущая 123 4 5 6 7 Следующая ⇒