
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Принцип действия асинхронного и синхронного двигателей
Устройство асинхронного двигателя соответствует изображению на рис. 4. Вращающееся магнитное поле, создаваемое расположенными на статоре обмотками с током, взаимодействует с токами ротора, приводя его во вращение. Наибольшее распространение в настоящее время получил асинхронный двигатель с короткозамкнутым ротором ввиду своей простоты и надежности. В пазах ротора такой машины размещены токонесущие медные или алюминиевые стержни. Концы всех стержней с обоих торцов ротора соединены медными или алюминиевыми же кольцами, которые замыкают стержни накоротко. Отсюда и произошло такое название ротора. В короткозамкнутой обмотке ротора под действием ЭДС, вызываемой вращающимся полем статора, возникают вихревые токи. Взаимодействуя с полем, они вовлекают ротор во вращение со скоростью Величина
называется относительным скольжением. Для двигателей нормального исполнения S=0, 02…0, 07. Неравенство скоростей магнитного поля и ротора становится очевидным, если учесть, что при Принципиальное отличие синхронного двигателя от асинхронного заключается в исполнении ротора. Последний у синхронного двигателя представляет собой магнит, выполненный (при относительно небольших мощностях) на базе постоянного магнита или на основе электромагнита. Поскольку разноименные полюсы магнитов притягиваются, то вращающееся магнитное поле статора, которое можно интерпретировать как вращающийся магнит, увлекает за собой магнитный ротор, причем их скорости равны. Это объясняет название двигателя – синхронный. В заключение отметим, что в отличие от асинхронного двигателя,
Литература
Контрольные вопросы
| ||
| Лекция N 22. Линейные электрические цепи при несинусоидальных периодических токах. |
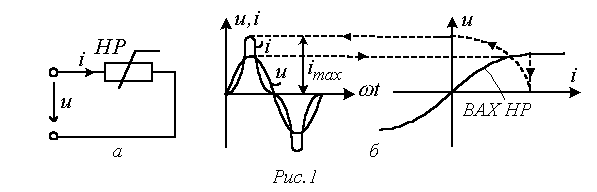
Предыдущие лекции были посвящены анализу электрических цепей при синусоидальных токах и напряжениях. На практике ЭДС и токи в большей или меньшей степени являются несинусоидальными. Это связано с тем, что реальные генераторы не обеспечивают, строго говоря, синусоидальной формы кривых напряжения, а с другой стороны, наличие нелинейных элементов в цепи обусловливает искажение формы токов даже при синусоидальных ЭДС источников.
На практике к несинусоидальности напряжений и токов следует подходить двояко:
 Характеристики несинусоидальных величин
Для характеристики несинусоидальных периодических переменных служат следующие величины и коэффициенты (приведены на примере периодического тока):
Характеристики несинусоидальных величин
Для характеристики несинусоидальных периодических переменных служат следующие величины и коэффициенты (приведены на примере периодического тока):
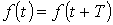 , где Т – период, удовлетворяющая условиям Дирихле, может быть разложена в тригонометрический ряд. Можно отметить, что функции, рассматриваемые в электротехнике, этим условиям удовлетворяют, в связи с чем проверку на их выполнение проводить не нужно.
При разложении в ряд Фурье функция представляется следующим образом: , где Т – период, удовлетворяющая условиям Дирихле, может быть разложена в тригонометрический ряд. Можно отметить, что функции, рассматриваемые в электротехнике, этим условиям удовлетворяют, в связи с чем проверку на их выполнение проводить не нужно.
При разложении в ряд Фурье функция представляется следующим образом:
Здесь В выражении (1)
Популярное:
|
Последнее изменение этой страницы: 2016-04-11; Просмотров: 673; Нарушение авторского права страницы