
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Общая методика расчета переходных процессов классическим методом
В общем случае методика расчета переходных процессов классическим методом включает следующие этапы:
Примеры расчета переходных процессов классическим методом
Рассмотрим два случая: а) б) Согласно рассмотренной методике для тока в цепи на рис. 2 можно записать
Тогда для первого случая принужденная составляющая тока
Характеристическое уравнение
откуда Таким образом,
Подставляя (4) и (5) в соотношение (3), запишем
В соответствии с первым законом коммутации
откуда Таким образом, ток в цепи в переходном процессе описывается уравнением
Качественный вид кривых При втором типе источника принужденная составляющая рассчитывается с использованием символического метода:
где Отсюда
Выражение свободной составляющей не зависит от типа источника напряжения. Следовательно,
Поскольку
Таким образом, окончательно получаем
Анализ полученного выражения (6) показывает:
Если
Таким образом, для линейной цепи максимальное значение тока переходного режима не может превышать удвоенной амплитуды принужденного тока: Аналогично для линейной цепи с конденсатором: если в момент коммутации принужденное напряжение равно своему амплитудному значению и постоянная времени
2. Переходные процессы при отключении катушки индуктивности
Характеристическое уравнение
откуда В соответствии с первым законом коммутации
Таким образом, выражение для тока в переходном режиме
и напряжение на катушке индуктивности
Анализ (7) показывает, что при размыкании цепей, содержащих индуктивные элементы, могут возникать большие перенапряжения, которые без принятия специальных мер могут вывести аппаратуру из строя. Действительно, при
При переводе ключа в положение 1 (см. рис. 6) начинается процесс заряда конденсатора:
Принужденная составляющая напряжения на конденсаторе Из характеристического уравнения
определяется корень Таким образом,
При t=0 напряжение на конденсаторе равно
Соответственно для зарядного тока можно записать
В зависимости от величины
При разряде конденсатора на резистор Тогда, принимая, что к моменту коммутации конденсатор был заряжен до напряжения
Соответственно разрядный ток
Как видно из (8), во избежание значительных бросков разрядного тока величина В заключение отметим, что процессы заряда и разряда конденсатора используются в генераторах пилообразного напряжения, широко применяемых в автоматике. Для этого ключ в схеме на рис. 6 заменяется на электронный. Литература
Контрольные вопросы
Ответ:
Ответ: | ||||||||||||||||
| Лекция N 25. Операторный метод расчета переходных процессов. |
Сущность операторного метода заключается в том, что функции 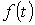 вещественной переменной t, которую называют оригиналом, ставится в соответствие функция вещественной переменной t, которую называют оригиналом, ставится в соответствие функция 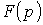 комплексной переменной комплексной переменной 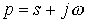 , которую называют изображением.В результате этого производные и интегралы от оригиналов заменяются алгебраическими функциями от соответствующих изображений (дифференцирование заменяется умножением на оператор р, а интегрирование – делением на него), что в свою очередь определяет переход от системы интегро-дифференциальных уравнений к системе алгебраических уравнений относительно изображений искомых переменных. При решении этих уравнений находятся изображения и далее путем обратного перехода – оригиналы. Важнейшим моментом при этом в практическом плане является необходимость определения только независимых начальных условий, что существенно облегчает расчет переходных процессов в цепях высокого порядка по сравнению с классическим методом.
Изображение , которую называют изображением.В результате этого производные и интегралы от оригиналов заменяются алгебраическими функциями от соответствующих изображений (дифференцирование заменяется умножением на оператор р, а интегрирование – делением на него), что в свою очередь определяет переход от системы интегро-дифференциальных уравнений к системе алгебраических уравнений относительно изображений искомых переменных. При решении этих уравнений находятся изображения и далее путем обратного перехода – оригиналы. Важнейшим моментом при этом в практическом плане является необходимость определения только независимых начальных условий, что существенно облегчает расчет переходных процессов в цепях высокого порядка по сравнению с классическим методом.
Изображение 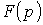 заданной функции заданной функции 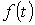 определяется в соответствии с прямым преобразованием Лапласа: определяется в соответствии с прямым преобразованием Лапласа:
В сокращенной записи соответствие между изображением и оригиналом обозначается, как:
Следует отметить, что если оригинал В качестве примера в табл. 1 приведены изображения некоторых характерных функций, часто встречающихся при анализе нестационарных режимов.
Таблица 1. Изображения типовых функций
Популярное:
|
Последнее изменение этой страницы: 2016-04-11; Просмотров: 821; Нарушение авторского права страницы