
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Переходная функция по напряжению
Переходная функция по напряжению наиболее часто используется при анализе четырехполюсников. Если линейную электрическую цепь с нулевыми начальными условиями подключить к источнику постоянного напряжения
где Переходную проводимость
В этой схеме
где Тогда переходная проводимость
Переходная функция по напряжению
Литература
Контрольные вопросы
Ответ:
| |||||
| Лекция N 27. Расчет переходных процессов с использованием интеграла Дюамеля. |
Зная реакцию цепи на единичное возмущающее воздействие, т.е. функцию переходной проводимости 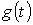 или (и) переходную функцию по напряжению или (и) переходную функцию по напряжению 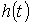 , можно найти реакцию цепи на воздействие произвольной формы. В основе метода – метода расчета с помощью интеграла Дюамеля – лежит принцип наложения.
При использовании интеграла Дюамеля для разделения переменной, по которой производится интегрирование, и переменной, определяющей момент времени, в который определяется ток в цепи, первую принято обозначать как , можно найти реакцию цепи на воздействие произвольной формы. В основе метода – метода расчета с помощью интеграла Дюамеля – лежит принцип наложения.
При использовании интеграла Дюамеля для разделения переменной, по которой производится интегрирование, и переменной, определяющей момент времени, в который определяется ток в цепи, первую принято обозначать как 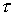 , а вторую - как t. , а вторую - как t.
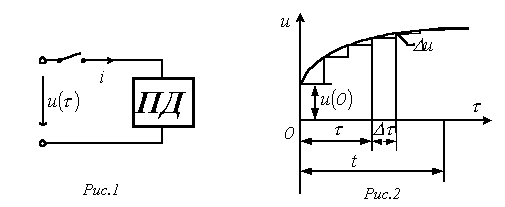 Пусть в момент времени
Пусть в момент времени 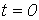 к цепи с нулевыми начальными условиями (пассивному двухполюснику ПДна рис. 1) подключается источник с напряжением к цепи с нулевыми начальными условиями (пассивному двухполюснику ПДна рис. 1) подключается источник с напряжением 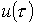 произвольной формы. Для нахождения тока произвольной формы. Для нахождения тока 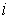 в цепи заменим исходную кривую ступенчатой (см. рис. 2), после чего с учетом, что цепь линейна, просуммируем токи от начального скачка напряжения в цепи заменим исходную кривую ступенчатой (см. рис. 2), после чего с учетом, что цепь линейна, просуммируем токи от начального скачка напряжения 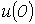 и всех ступенек напряжения до момента t, вступающих в действие с запаздыванием по времени.
В момент времени t составляющая общего тока, определяемая начальным скачком напряжения и всех ступенек напряжения до момента t, вступающих в действие с запаздыванием по времени.
В момент времени t составляющая общего тока, определяемая начальным скачком напряжения 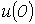 , равна , равна 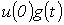 .
В момент времени .
В момент времени 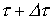 имеет место скачок напряжения имеет место скачок напряжения 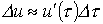 , который с учетом временного интервала от начала скачка до интересующего момента времени t обусловит составляющую тока , который с учетом временного интервала от начала скачка до интересующего момента времени t обусловит составляющую тока 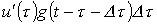 .
Полный ток .
Полный ток 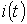 в момент времени t равен, очевидно, сумме всех составляющих тока от отдельных скачков напряжения с учетом в момент времени t равен, очевидно, сумме всех составляющих тока от отдельных скачков напряжения с учетом 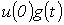 , т.е. , т.е.
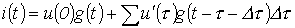 .
Заменяя конечный интервал приращения времени .
Заменяя конечный интервал приращения времени 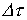 на бесконечно малый, т.е. переходя от суммы к интегралу, запишем на бесконечно малый, т.е. переходя от суммы к интегралу, запишем
Соотношение (1) называется интегралом Дюамеля. Следует отметить, что с использованием интеграла Дюамеля можно определять также напряжение. При этом в (1) вместо переходной проводимости
Последовательность расчета с использованием
Исходные данные для расчета:
Полученный результат аналогичен выражению тока, определенному в предыдущей лекции на основе формулы включения.
Метод переменных состояния Уравнения элекромагнитного состояния – это система уравнений, определяющих режим работы (состояние) электрической цепи. Метод переменных состояния основывается на упорядоченном составлении и решении системы дифференциальных уравнений первого порядка, которые разрешены относительно производных, т.е. записаны в виде, наиболее удобном для применения численных методов интегрирования, реализуемых средствами вычислительной техники. Количество переменных состояния, а следовательно, число уравнений состояния равно числу независимых накопителей энергии. К уравнениям состояния выдвигаются два основных требования: -независимость уравнений; -возможность восстановления на основе переменных состояния (переменных, относительно которых записаны уравнения состояния) любых других переменных. Первое требование удовлетворяется специальной методикой составления уравнений состояния, которая будет рассмотрена далее. Для выполнения второго требования в качестве переменных состояния следует принять потокосцепления (токи в ветвях с индуктивными элементами) и заряды (напряжения) на конденсаторах. Действительно, зная закон изменения этих переменных во времени их всегда можно заменить источниками ЭДС и тока с известными параметрами. Остальная цепь оказывается резистивной, а следовательно, всегда рассчитывается при известных параметрах источников. Кроме того, начальные значения этих переменных относятся к независимым, т.е. в общем случае рассчитываются проще других. При расчете методом переменных состояния, кроме самих уравнений состояния, связывающих первые производные Таким образом, полная система уравнений в матричной форме записи имеет вид
Здесь Начальные условия для уравнения (2) задаются вектором начальных значений В качестве примера составления уравнений состояния рассмотрим цепь на рис. 4, а, в которой требуется определить токи
По законам Кирхгофа для данной цепи запишем
Поскольку
или в матричной форме записи
Матричное уравнение вида (3) вытекает из соотношений (4) и (6):
Вектор начальных значений Непосредственное использование законов Кирхгофа при составлении уравнений состояния для сложных цепей может оказаться затруднительным. В этой связи используют специальную методику упорядоченного составления уравнений состояния.
Популярное:
|
Последнее изменение этой страницы: 2016-04-11; Просмотров: 783; Нарушение авторского права страницы