Аналитические методы расчета

⇐ ПредыдущаяСтр 23 из 29Следующая ⇒

Аналитические методы, в отличие от рассмотренных выше графических, позволяют проводить анализ нелинейной цепи в общем виде, а не для частных значений параметров элементов схемы. В этом заключается их главное преимущество. Однако аппроксимация нелинейной характеристики, лежащая в основе данных методов, изначально обусловливает внесение в расчеты большей или меньшей погрешности. Как и при графическом анализе цепей, при применении аналитических методов используются характеристики нелинейных элементов для мгновенных значений, по первым гармоникам и для действующих значений. При этом для расчета цепей переменного тока наиболее широкое распространение получили следующие аналитические методы:

-метод аналитической аппроксимации;

-метод кусочно-линейной аппроксимации;

-метод гармонического баланса;

-метод эквивалентных синусоид (метод расчета по действующим значениям).

В первых трех случаях обычно используются характеристики нелинейных элементов для мгновенных значений. Характеристики нелинейных элементов по первым гармоникам используются при применении частного варианта метода гармонического баланса - метода расчета по первым гармоникам. В свою очередь, метод эквивалентных синусоид основан на применении характеристик нелинейных элементов для действующих значений.

Метод аналитической аппроксимации

Данный метод основан на аппроксимации характеристик нелинейных элементов аналитическими выражениями с последующим аналитическим решением системы нелинейных уравнений состояния цепи. Точность, а с другой стороны, сложность расчета методом аналитической аппроксимации непосредственно зависят от вида принятой аналитической функции, аппроксимирующей характеристику нелинейного элемента. Поэтому ее выбор является важнейшим этапом при анализе цепи данным методом. Как уже отмечалось, для получения большей точности расчета необходимо выбирать аппроксимирующую функцию, наиболее полно соответствующую исходной нелинейной характеристике, что, однако, может привести в общем случае к появлению в уравнениях состояния сложных математических выражений, часто трудно разрешимых (или вообще неразрешимых) аналитически. С другой стороны, принятие чрезмерно простой функции для аппроксимации позволяет достаточно быстро получить результат, однако погрешность расчета может оказаться недопустимо высокой. Таким образом, выбор аппроксимирующей функции во многом зависит от поставленной задачи расчета и требуемой точности его результатов.

Пусть, например, в цепи состоящей из последовательно соединенных источника тока с и нелинейной катушки индуктивности, заданная графически вебер-амперная характеристика которой может быть аппроксимирована выражением

(3)

требуется найти напряжение на индуктивном элементе.

На первом этапе определяем коэффициенты и аппроксимирующей функции с учетом того, что рабочий участок заданной графически кривой ограничен сверху амплитудой А тока в цепи, что сразу дает одну из двух точек аппроксимации.

После этого подставляем в (3) выражение , в результате чего получаем

или, с учетом соотношения

Тогда искомое напряжение на катушке индуктивности

Литература

Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
Теоретические основы электротехники. Учеб. для вузов. В трех т. Под общ. ред. К.М.Поливанова. Т.2. Жуховицкий Б.Я., Негневицкий И.Б. Линейные электрические цепи (продолжение). Нелинейные цепи. –М.: Энергия- 1972. –200с.
Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.

Контрольные вопросы и задачи

В чем состоит сущность графического метода расчета с использованием характеристик по первым гармоникам?
На чем основан метод эквивалентных синусоид?
В каком случае и как метод эквивалентных синусоид можно применять для анализа цепей с инерционными нелинейными элементами?
Какие цепи относятся к феррорезонансным?
Что называется феррорезонансом напряжений? С помощью чего можно обеспечить данный режим?
Что называется феррорезонансом токов? С помощью чего можно обеспечить данный режим?
В чем заключается эффект опрокидывания фазы?
Как можно экспериментально снять участки 4-6 и 2-5 на рис. 2 и участок 1-3 на рис. 6?
Для заданной на рис. 2 кривой построить зависимость , обеспечивающую скачок тока с увеличением напряжения при заданной величине последнего. При решении принять .
Для заданной на рис. 6 кривой построить зависимость , обеспечивающую триггерный эффект при заданной величине тока.

Лекция N 34. Метод кусочно-линейной аппроксимации.

В соответствии с определением данного метода, расчет нелинейной цепи с его использованием включает в себя в общем случае следующие основные этапы: 1. Исходная характеристика нелинейного элемента заменяется ломаной линией с конечным числом прямолинейных отрезков. 2. Для каждого участка ломаной определяются эквивалентные линейные параметры нелинейного элемента и рисуются соответствующие линейные схемы замещения исходной цепи. 3. Решается линейная задача для каждого отрезка в отдельности.

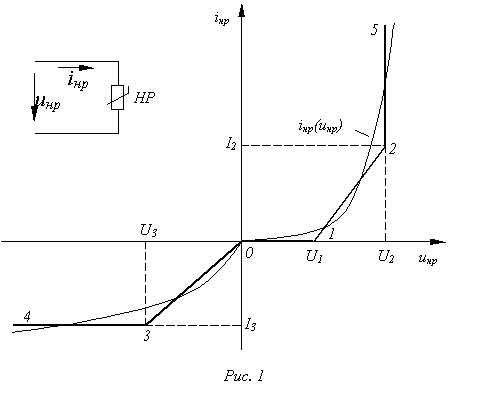
4. На основании граничных условий определяются временные интервалы движения изображающей точки по каждому прямолинейному участку (границы существования отдельных решений). Пусть вольт-амперная харак-теристика (ВАХ) нелинейного резистора имеет форму, представленную на рис. 1. Заменяя ее ломаной линией 4-3-0-1-2-5, получаем приведенные в табл. 1 расчетные эквивалентные схемы замещения и соответ-ствующие им линейные соотношения. Расчет каждой из полученных линейных схем замещения при наличии в цепи одного нелинейного элемента и произвольного числа линейных не представляет труда. В этом случае на основании теоремы об активном двухполюснике исходная нелинейная цепь сначала сводится к схеме, содержащей эквивалентный генератор с некоторым линейным внутренним сопротивлением и последовательно с ним включенный нелинейный элемент, после чего производится ее расчет. При наличии в цепи переменного источника энергии рабочая (изображающая) точка будет постоянно скользить по аппроксимирующей характеристике, переходя через точки излома. Переход через такие точки соответствует мгновенному изменению схемы замещения. Поэтому задача определения искомой переменной сводится не только к расчету схем замещения, но и к определению моментов “переключения” между ними, т.е. нахождению граничных условий по времени. Анализ существенно усложняется, если в цепи имеется несколько нелинейных элементов. Главная трудность в этом случае связана с тем, что заранее не известно сочетание линейных участков, соответствующее заданному входному напряжению (току). Искомое сочетание линейных участков всех нелинейных элементов определяется перебором их возможных сочетаний. Для любого принятого сочетания параметры схемы известны, и, следовательно, могут быть определены напряжения и токи для всех элементов. Если они лежат в пределах соответствующих линейных участков, то принятое сочетание дает верный результат. Если хотя бы у одного нелинейного элемента переменные выходят за границы рассматриваемого линейного участка, то следует перейти Таблица 1. Кусочно-линейная аппроксимация ВАХ нелинейного резистора

Участок аппроксимирующей кривой

Схема замещения

Параметры элементов

Граничные условия

0 - 1

1 - 2

2 - 5

3 - 0

2 - 5

к другому сочетанию. Необходимо отметить, что всегда имеется единственное сочетание линейных участков характеристик нелинейных элементов, соответствующее изменению входного сигнала в некоторых пределах.

В качестве примера определим напряжение в цепи на рис. 2, в которой . ВАХ нелинейного резистора приведена на рис. 3, где .

Решение

1. В соответствии с заданной ВАХ нелинейный резистор на участке 1-2 заменяем линейным резистором с сопротивлением

на участке 2-3-источником тока с током и на участке 4-1-источником тока с током .

2. На основании данной эквивалентной замены для тока на участке 1-2 ВАХ можно записать:

(1)

откуда

При движении изображающей точки по участку 2-3 ВАХ имеем

при движении по участку 1-4 ВАХ-

3. Определяем интервалы движения изображающей точки по отдельным участкам ВАХ. Для точки излома 1 на основании (1) справедливо уравнение

или

Отсюда получаем два значения мгновенной фазы питающего напряжения на одном периоде, соответствующих точке 1: . Первое значение определяет переход изображающей точки с участка 4-1 на участок 1-2, второе – с участка 2-1 на участок 1-4.

Аналогично записываем для точки 2 излома ВАХ

или

откуда (значение, соответствующее переходу с участка 1-2 на участок 2-3) и (значение, соответствующее переходу с участка 3-2 на участок 2-1).

Таким образом, получаем для одного периода питающего напряжения

;

В соответствии с периодичностью синусоидальной функции данные решения повторяются через 360°n.

На рис. 4 представлен график зависимости искомой величины.

⇐ Предыдущая 18 19 20 21 222324 25 26 27 Следующая ⇒