Метод аналитической аппроксимации

⇐ ПредыдущаяСтр 26 из 29Следующая ⇒

Метод основан на аппроксимации характеристики нелинейного элемента аналитической функцией, которая должна, с одной стороны, достаточно точно отображать исходную нелинейную характеристику на участке перемещения рабочей точки, а с другой стороны, обеспечивать возможность достаточно несложного интегрирования полученного дифференциального уравнения (в частности, с использованием табличных интегралов).

Метод применим к нелинейным цепям с одним накопителем энергии, описываемым дифференциальными уравнениями первого порядка, а также к цепям, описываемым уравнениями, сводящимися к уравнениям первого порядка путем замены переменных.

Ценность метода заключается в получении выражения исследуемой величины в общем виде, что позволяет осуществлять требуемый анализ процессов при варьировании параметров схемы.

В качестве примера использования метода определим ток в схеме на рис. 3, полагая, что характеристика нелинейной катушки имеет вид типовой кривой на рис. 2.

1. Для решения задачи выберем выражение аналитической аппроксимации вида . Определяя параметр из условия соответствия данной функции точке установившегося послекоммутационного режима, получим

(4)

где .

2. Подставив в уравнение переходного процесса

аналитическое выражение тока с учетом (4), получим

(5)

Разделяя переменные и решая (5) относительно времени, запишем

(6)

где – начальное значение потокосцепления, соответствующее значению тока в момент коммутации .

Выражение (6) соответствует табличному интегралу; в результате получаем

(7)

Подставив в последнее соотношение выражение потокосцепления в виде

перепишем (7) как

Метод кусочно–линейной аппроксимации

Данный метод основан на замене характеристики нелинейного элемента отрезками прямых, на основании чего осуществляется переход от нелинейного дифференциального уравнения к нескольким (по числу прямолинейных отрезков) линейным, которые отличаются друг от друга только значениями входящих в них коэффициентов. Необходимо помнить, что каждое из линейных уравнений справедливо для того временного интервала, в течение которого рабочая точка перемещается по соответствующему линеаризованному участку. Временные границы для каждого участка определяются исходя из достижения одной (любой) из переменных, определяющих характеристику нелинейного элемента, своих граничных значений для рассматриваемого прямолинейного участка. В соответствии с законами коммутации значения тока в ветви с катушкой индуктивности или напряжения на конденсаторе в эти моменты времени являются начальными значениями соответствующих переменных для соседних прямолинейных участков, на основании чего определяются постоянные интегрирования. Значение параметра линеаризуемого нелинейного элемента для каждого участка ломаной определяется тангенсом угла, образованного рассматриваемым прямолинейным отрезком с соответствующей осью системы координат.

В качестве примера рассмотрим применение данного метода для решения предыдущей задачи.

1. Заменим рабочий участок зависимости (см. рис. 2) двумя прямолинейными отрезками и . Первому из них соответствует уравнение , второму – . При этом начальная точка определяется током , а конечная точка - током .

Соответствующие этим участкам индуктивности

;

2. В соответствии с указанной линеаризацией нелинейное дифференциальное уравнение состояния цепи

заменяется двумя линейными:

;

3. Решением первого уравнения является

и второго -

где ; ; ; .

Время t1, соответствующее моменту перехода с первого участка на второй, определим из уравнения

откуда

Литература

Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
Теоретические основы электротехники. Учеб. для вузов. В трех т. Под общ. ред. К.М.Поливанова. Т.2. Жуховицкий Б.Я., Негневицкий И.Б. Линейные электрические цепи (продолжение). Нелинейные цепи. –М.: Энергия- 1972. –200с.
Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.

Контрольные вопросы и задачи

В чем заключаются особенности расчета переходных процессов в нелинейных цепях?
В чем состоит сущность метода условной линеаризации? С чем связана его невысокая точность?
В чем заключается основное преимущество метода аналитической аппроксимации?
Следует ли применять метод кусочно-линейной аппроксимации для расчета переходных процессов в цепях с питанием от источника переменного напряжения?
Аппроксимируя зависимость выражением , определить ток в цепи на рис. 1 при ее включение на постоянное напряжение .

Ответ: .

Заменив в цепи на рис. 1 нелинейную катушку индуктивности на нелинейный конденсатор с характеристикой , подобной на рис. 2, методом кусочно-линейной аппроксимации определить зависимость .

Лекция N 37. Графические методы анализа переходных процессов в нелинейных цепях.

Графическими называются методы, в основе которых лежат графические построения на плоскости. По сравнению с рассмотренными выше аналитическими методами они обладают следующими основными преимуществами: - отсутствием принципиальной необходимости в аналитическом выражении характеристики нелинейного элемента, что устраняет погрешность, связанную с ее аппроксимацией; - возможностью проведения расчетов при достаточно сложных формах кривых нелинейных характеристик. Главный недостаток графических методов заключается в получении решения для конкретных значений параметров цепи. Основными графическими методами, используемыми при решении электротехнических задач, являются: 1. Метод графического интегрирования Метод графического интегрирования основан на графическом подсчете определенного интеграла и заключается в последовательном нахождении площадей под соответствующей подынтегральной функции кривой. Он применяется для анализа электрических цепей, переходные процессы в которых описываются дифференциальными уравнениями первого порядка с разделяющимися переменными. 2. Метод изоклин Данный метод является одним из наиболее широко используемых графических методов приближенного интегрирования. Он непосредственно используется для решения уравнений первого порядка вида

и при этом включает в себя в общем случае следующие этапы: в плоскости

по уравнениям изоклин

(изоклина - линия равного наклона, вдоль которой функция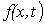

имеет постоянное значение, т.е. геометрическое место точек, для которых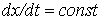

) строятся изоклины для различных значений углового коэффициента

; вдоль каждой изоклины наносятся черточки с наклоном, определяемым соответствующим значением

; от точки

соответствующей начальному условию, строится интегральная кривая так, чтобы она пересекала каждую изоклину параллельно нанесенным на ней черточкам; полученная кривая является графиком искомой зависимости

3. Метод фазовой плоскости Метод позволяет осуществлять качественное исследование динамических процессов в нелинейных цепях, описываемых дифференциальными уравнениями первого и второго порядков. При этом без непосредственного интегрирования нелинейных дифференциальных уравнений данный метод дает возможность получить представление о процессе в целом. В общем случае исследования, проводимые методом фазовой плоскости, позволяют выявить зависимость характера переходного процесса от начальных условий, судить об устойчивости или неустойчивости работы цепи, устанавливать возможность появления в цепи автоколебаний с оценкой их частоты и формы и т. д. Более подробно с графическими методами можно познакомиться в [1, 2, 3]. Численные методы расчета переходных процессов Численные методы анализа динамических процессов в нелинейных электрических цепях базируются на различных численных способах приближенного интегрирования нелинейных дифференциальных уравнений. В их основе лежит общий принцип: исходное дифференциальное уравнение заменяется алгебраическим для приращений зависимой (исследуемой) переменной за соответствующие интервалы изменения независимой переменной (времени). Основным достоинством численных методов является их универсальность, т.е. принципиальная пригодность для анализа любой цепи. Это особенно важно в случае нелинейных цепей, для которых не существует общих аналитических методов расчета. Применительно к анализу динамических процессов в нелинейных цепях наибольшее распространение получили: - метод переменных состояния; - метод дискретных моделей. Метод переменных состояния Метод переменных состояния, как было показано при анализе переходных процессов в линейных цепях, основывается на составлении и интегрировании дифференциальных уравнений, записанных в нормальной форме. Полная система уравнений в матричной форме имеет вид

(1)

Здесь и - матрицы переменных состояния и их первых производных по времени соответственно; w(z ) – матрица нелинейных резистивных элементов; z – матрица аргументов нелинейных резистивных элементов; v – матрица входных воздействий ( ЭДС и токов источников ); y – матрица искомых величин.

При составлении уравнений состояния для относительно несложных цепей они могут быть записаны непосредственно по законам Кирхгофа. В общем же случае для этой цели используется или методика, основанная на составлении по специальному алгоритму таблицы соединений, что было показано при рассмотрении метода переменных состояния применительно к расчету линейных цепей, или методика, базирующаяся на принципе наложения.

⇐ Предыдущая 20 21 22 23 24 252627 28 29 Следующая ⇒