Виды испытания на надежность

В зависимости от цели проведения испытания на надежность делят на определительные(исследовательские)и контрольные.

Цель определительных испытаний – нахождение фактических значений показателей надежности и при необходимости параметров законов распределения таких случайных величин, как время безотказной работы, наработка между отказами, время восстановления, частота отказов и др.

Цель контрольных испытаний – проверка соответствия фактических значений показателей надежности требованиям стандартов (СТРК), технических заданий (ТЗ) и технических условий (ТУ), т.е. принятие решения типа «да - нет» о соответствии или несоответствии надежности системы предъявленным требованиям.

Кроме оценки показателей надежности, целями испытаний обычно являются: изучение причин и закономерностей возникновения отказов; выявление конструктивных, технологических и эксплуатационных факторов, влияющих на надежность; выявление наименее надежных элементов, узлов, блоков, технических средств; разработка мероприятий и рекомендаций по повышению надежности; уточнение продолжительности и объема технического обслуживания, количества запасных частей и другое.

Испытания надежности можно проводить в лабораторных (стендовых) и эксплуатационных условиях. Испытаниям надежности в лабораторных условиях обычно подвергаются технические средства и некоторые локальные системы.

Эти испытания обычно выполняются на заводах – изготовителях или в организациях – разработчиках технических средств, они могут быть как определительными, так и контрольными.

При лабораторных испытаниях можно имитировать воздействия внешней среды на систему, в первую очередь условия эксплуатации.

Для этого служат специальные установки: термокамеры для изменения температуры, барокамеры для изменения давления, вибростенды для создания вибраций и т.д.

Лабораторные испытания могут проходить при тех же воздействиях (температуре, влажности, вибрации и т.д.) и режимах работы, которые имеют место при эксплуатации.

Испытания надежности в условиях эксплуатации заключаются в сборке и обработке информации о поведении автоматизированных систем и их элементов и о воздействии внешней среды при опытной и (или) промышленной эксплуатации совместно с действующим технологическим объектом управления. Эти испытания обычно являются определительными.

Оба вида испытаний – эксплуатационные и лабораторные – дополняют друг друга.

Преимуществами эксплуатационных испытаний являются: естественный учет влияния воздействий внешней среды, например температуры, вибрации, квалификации оперативного и ремонтного персонала; низкая стоимость испытаний, так как их проведение не требует дополнительных затрат на оборудование, имитирующее условия эксплуатации (полигоны при заводах – изготовителях), что позволяет в сравнительно короткие сроки получить статистически достоверную информацию.

Недостатками эксплуатационных испытаний по сравнению с лабораторными являются: невозможность проводить активный эксперимент, изменяя по желанию экспериментатора параметры внешней среды для систем; ниже достоверность информации; меньше оперативность информации, так как начало ее получения может иметь место после изготовления всех технических средств, монтажа и наладки систем.

Исходной информацией для статистического исследования, на основании которого должны быть сделаны выводы о показателях надежности, служат результаты наблюдений.

Эти результаты могут быть разными для одних и тех же систем в зависимости от того, каким образом они были получены.

Перед началом испытаний необходимо выработать правило, согласно которому следует проводить испытания. Выработку такого правила будет называться планированием испытаний. Выбор плана диктуется целями поставленных испытаний.

Кроме расчетных и экспериментальных методов оценки показателей надежности имеет место и расчетно – экспериментальные методы. Такие методы применяют, если по техническим, экономическим и организационным причинам невозможно или нецелесообразно применять экспериментальные методы, например для систем, которые нельзя испытать в полном объеме.

Определительные испытания

Определительным испытаниям могут подвергаться автоматизированные системы управления в целом, их подсистемы, функции, технические средства и любые другие элементы систем.

Перед началом определительных испытаний составляется план испытаний. Планом испытаний называют правила, устанавливающие объем выборки, порядок их проведения испытаний и критерии их прекращения. Рассмотрим наиболее распространенные планы определительных испытаний. Наименование плана принято обозначать тремя буквами (цифрами): первая из них обозначает число испытуемых систем, вторая – наличие R или отсутствие U восстановлений на время испытаний в случае отказа, третья – критерий прекращения испытаний.

План [NUŤ ] соответствует одновременному испытанию систем. Эти системы после отказа не восстанавливаются (или же восстанавливаются, но данные о их поведении после первого отказа в испытаниях не рассматриваются). Испытания прекращают по истечении наработки каждой отказавшей системы. На рисунке 9.1, а знаком «х» обозначено наличие отказа; t_i - наработка до отказа i–ой системы. Этот план обычно применяют для определения вероятности безотказной работы системы за время Ť.

а) б)

в) г)

Рисунок 9.1 – Планы испытаний

Испытания прекращают по истечении наработки каждой отказавшей системы. Этот план обычно применяют для определения вероятности безотказной работы системы за указанное время Ť.

План [NUr]– соответствует испытаниям N таких же невосстанавливаемых систем, однако в отличие от плана[NUT] испытание прекращают, когда число отказавщих систем достигает r. На рисунке 9.1, б, r -ый отказ имеет место у i–ой системы. Если r = N, переходим к плану [NUN], когда испытания прекращаются после отказов всех систем.

План [NUr] обычно применяют для определения средней наработки до отказа в случае экспоненциального распределения, а план [NUN] – в случае нормального распределения. Испытания по плану [NUN] требуют значительных времени и числа испытываемых систем, но дают возможность полностью определить эмпирическую функцию распределения. Планы [NUr], [NUŤ ] позволяют определить эмпирическую функцию распределения только для некоторого интервала времени, дают меньше информации, зато позволяют быстрее закончить испытания.

План [NRŤ ]– описывает испытания N систем причем отказавшие во время испытаний системы заменяют новым или восстанавливают. Испытания прекращают по истечении наработки Ť каждой из позиций (под позицией понимаем определенное место на стенде или объекте, применительно к которому наработка исчисляется независимо от произошедших на данной позиции замен или восстановлений – рисунок 9.1, в)

План [NRr] – соответствует испытанияv N систем, когда отказавшие во время испытаний системы заменяют новыми или восстанавливают. Испытание прекращают, когда суммарное по всем позициям число отказавших систем достигает r (рисунок 9.1, г).

Задачами планирования является определение минимального объема наблюдений – выбор числа испытываемых систем N, а также продолжительности наблюдений Ť для планов [NUŤ ] и [NRŤ ]или числа отказов r для планов [NUr] и [NRr].

Результатами определительных испытаний должны являться точечные и интервальные оценки показателей надежности.

Точечная оценка понятие математической статистики. Пусть имеются результаты k наблюдений t₁, t₂, ….t_kнад некоторой случайной величиной Т с функцией распределения F(t, υ ), причем праметр υ этого распределения неизвестен. Необходимо найти такую функцию ῦ =g(t₁, t₂, ….t_k) результатов наблюдений t₁, ….t_k_, которую можно было рассматривать как оценку параметра υ. При таком выборе финкций g каждой совокупности (t₁, ….t_k) будет соответствовать точка ῦ на числововй оси, которую называют точечной оценкой параметра υ.

Статистические определения показателей надежности, приведенные в лекции 2, являются их точечными оценками. При этом оценка средней наработки до отказа, соответствует плану [NUN], так как здесь рассматриваются завершенные (не прерванные в испытаниях) наработки до отказа каждой из испытуемых систем.

(9.1)

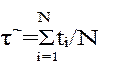
Это соотношение имеет место при любых законах распределения наработки до отказа.

Для экспоненциального распределения, кроме плана [NUN] , точечная оценка средней наработки до отказа:

(9.2)

где S - суммарная наработка всех систем за время испытаний; n_S - суммарное число отказов всех систем на время испытаний.

Например, при плане [NUŤ ]

(9.3)

где L - число систем, отказавших на интервале (0, Ť ); t_i - наработка до отказа i– той системы из числа отказавших (i=1, L).

При плане [NUr]

(9.4)

(9.5)

Для плана [NRT] и простейшего потока

Оценка интенсивности отказов λ ˜ при экспоненциальном распределении согласно (3.6) может быть определена через оценку средней наработки до отказа: . Например, при плане [NUN] .

(9.6)

При плане [NRT] оценка параметра потока отказов

совпадает с оценкой интенсивности отказов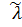

При нормальном распределении и плане [NUN]:

(9.7)

(9.8)

Для рассмотрения точности оценки вводится понятие доверительного интервала. Интервальные оценки заключается в определение доверительного интервала. Примем, что имеются результаты k наблюдений t₁, t_2…, t_k над случайной величиной Т с функцией распределения F(t, V), где параметр V неизвестен. Необходимо найти такую функцию V_н=g_н(t₁, t_2…, t_k) результатов наблюдений, чтобы интервал (V_н, ∞ ) накрывал неизвестный параметр V с заданной вероятностью γ ₁:

Величину V_Нназывают нижней доверительной границей параметра V при односторонней доверительной вероятности γ ₁_.

Для заданной вероятности γ ₂ по той же совокупности наблюдений может быть найдена функция V_вр = g_вр(t₁, t_2…, t_k) такая, что интервал (0, V_вр) накрывает параметр V с вероятностью γ ₂:

(9.9)

Величину V_ВРназывают верхней доверительной границей параметра V при односторонней доверительной вероятности γ _2.

Нижняя и верхняя доверительные границы образуют доверительный интервал, который с вероятностью γ накрывает на числовой оси неизвестное значение параметра V. При γ ₁> 0, 5 и γ ₂> 0, 5 (доверительные вероятности γ ₁ и γ ₂обычно выбираются не менее 0, 8) согласно (9.8) и (9.9):

где γ ₌γ ₁+ γ ₂ -1; Обычно принимают, что γ ₁= γ _2,тогда γ = 2 γ ₁ – 1.

Значение доверительного интервала тем меньше. Чем больше число наблюдений (например, чем больше число отказов при испытаниях) и чем меньше значение γ доверительной вероятности.

Определение границ доверительного интервала заключается в следующем. Так как оценка неизвестного параметра V является случайной величиной, то находим закон ее распределения. Затем определяем интервал (V_Н, V_ВР), в которой случайная величина попадает с вероятностью γ.

Контрольные испытания

Контрольным испытаниям обычно подвергаются подсистемы, технические средства и их элементы. Для технических средств обязательными являются контрольные испытания на безотказность.

Испытания на ремонтопригодность, сохраняемость и долговечность проводят в тех случаях, когда это предусмотрено стандартами, техническими заданиями или техническими условиями на конкретный прибор (средства).

Периодичность контрольных испытаний на безотказность обычно не реже одного раза в три года.

Для проведения контрольных испытаний из совокупности (партия) однородных приборов составляется некоторая выборка и проводятся испытания на надежность попавших в эту партию приборов.

По результатам испытания выборки выносится суждение о соответствии всей партии предъявленным требованиям.

Математический аппарат решения задачи – изучаемые в математической статистике методы проверки статистических гипотез.

В качестве проверяемой (или, как принято говорить, нулевой) гипотезы принимается предположение, что партия соответствует требованиям к надежности, в качестве противоположной (альтернативной) – что партия не удовлетворяет этим требованиям.

По результатам испытаний имеет место одна из следующих четырех ситуаций:

1. Партия удовлетворяет требованиям; по результатам испытаний подтвердилась нулевая гипотеза и принято решение о принятии партии. Это решение правильно.

2. Партия удовлетворяет требованиям, но по результатам испытаний нулевая гипотеза не подтвердилась. Это произошло потому, что случайно составленная выборка содержала повышенное число отказавших приборов по сравнению с совокупностью. Принята альтернативная гипотеза; это решение неправильно и невыгодно для изготовителя приборов. При этом произошла ошибка, вероятность которой называют риском поставщика (изготовителя) α.

3. Партия не удовлетворяет требованиям, по результатам испытаний нулевая гипотеза не подтвердилась. Принята альтернативная гипотеза, т.е. решение о неприятии партии. Это решение правильно.

4. Партия не удовлетворяет требованиям, но по результатам испытаний подтвердилась нулевая гипотеза о соответствии требованиям надежности, так как выборка содержала повышенное число неотказавших приборов по сравнению со всей партией. Принято решение, но оно не выгодно в отличие от п. 2 не изготовителю, а потребителю – заказчику эти приборов. Произошла ошибка, вероятность которой называют риском потребителя (заказчика) β.

Естественно, что желательно снизить значения обеих ошибок, доведя их до нуля. Зависимость вероятности L приемки партии от показателя надежности А ( называемой оперативной характеристикой плана контроля) для такой предельной ситуации дана на рисунке 9.2, а. Пусть А_тр – требуемое значение показателя надежности. В этой ситуации нулевая гипотеза А≥ А_тр. Если она справедлива, то партия принимается с вероятностью равной единице, причем α =0. Альтернативная гипотеза заключается в том, что А£ А_тр. При этом партия бракуется с вероятностью, равной единице, причем β =0.Однако такая идеальная оперативная характеристика недостижима, так как требует бесконечного объема наблюдений.

В реальной ситуации вводятся два уровня контролируемого показателя надежности: приемочный А_α и браковочный А_β(рисунок 9.2, б).

а) б)

Рисунок 9.2 – Идеальная (а) и реальная (б) оперативные характеристики планов контроля

Если А≥ А_α, то приборы должны приниматься с достаточно высокой вероятностью, не ниже L(А_α), если А£ А_β, то приборы должны браковаться с достаточно высокой вероятностью, не ниже 1 – L(А_β). При этом риск поставщика α =1-L(А_α), риск потребителя β =1-L(А_β). Тем самым проверку нулевой гипотезы А≥ А_трпри альтернативе А£ А_тр заменяем другой задачей – проверкой нулевой гипотезы А≥ А_α при альтернативе А£ А_β. Чем ближе А_α к А_β, тем больший объем испытаний необходим для принятия достоверного решения о соответствии партии.

Значение браковочного уровня А_β устанавливается с учетом приемочного уровня А_α, стоимости, продолжительности и условий испытаний и т.п.

Риск поставщика α и потребителя β обычно принимается равным 0, 1-0, 2, но в принципе по согласованию между потребителем и поставщиком возможен выбор и иных значений α и β.

Контрольные испытания на безотказность проводятся обычно одно- или двухступенчатым методом. При применении первого из них испытания выполняют следующим образом. Образцы, вошедшие в выборку объема d, испытывают в течение времени t_и. По окончании испытаний определяют число наступивших отказов n. Если оно равно или меньше приемочного числа с, определенного в зависимости от величины А_α, А_β, α и β, то нулевая гипотеза подтверждается и партию принимают. Если же n> с, то подтверждается альтернативная гипотеза и партию не принимают. Одноступенчатый метод при прочих равных условиях обеспечивает минимальную календарную продолжительность испытаний, двухступенчатый при тех же условиях позволяет обеспечить минимум среднего объема испытаний.

Лекция 10

Цель лекции: Обучение основным методам повышения надежности на этапе проектирования и эксплуатации.

⇐ Предыдущая 1 2 3 4 5 678 9 10 Следующая ⇒