
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Показатели надежности технических систем.Стр 1 из 10Следующая ⇒
ЛЕКЦИЯ 1 Цель лекции: Ознакомление с основными понятиями теории надежности. Введение в теорию надежности. Основные термины и определения теории надежности. 1.1 Введение. Основные понятия и определения теории надежности. Теория надежности – научная дисциплина, в которой изучаются методы обеспечения эффективности работы объектов (устройств, систем)в процессе эксплуатации. Теория надежности (ТН) появилась в середине 40-х годов 20-века и использовалась для необходимых расчетов надежности систем управления и различных видов связи. Постепенно она нашла применение во многих областях человеческой деятельности (машиностроение, транспорт, строительство, энергетика, системы управления). Технические средства и условия их работы становятся все более сложными. Количество элементов в отдельных видах устройств исчисляется сотнями тысяч. Если не принимать специальных мер по обеспечению надежности, то любое современное сложное устройство практически будет неработоспособным. Наука о надежности развивается в тесном взаимодействии с другими науками. Прежде всего, она тесно связана с проектированием информационных систем и вопросами обеспечения их безопасности. Среди математических дисциплин, прежде всего наибольшее применение получили: теория вероятности; некоторые элементы дискретной математики; дифференциальные уравнения и интегральные исчисления. В настоящее время теория надежности является самостоятельной научной дисциплиной. Основные ее задачи: установление видов количественных показателей надежности; выработка методов аналитической оценки надежности; разработка методов оценки надежности по результатам испытаний; оптимизация надежности на стадиях разработки и эксплуатации технических систем. 1.2 Основные термины и определения. Надежность- свойство объекта (системы) сохранять во времени в установленных пределах значения всех параметров, характеризующих способность выполнять требуемые функции в заданных режимах и условиях эксплуатации. Техническая система– совокупность элементов, взаимодействующих между собой в процессе выполнения заданных функций. Элемент системы–составная часть любой системы, которая рассматривается без дальнейшего разделения как единое целое; внутренняя структура элемента не является предметом исследования. Понятия «система» и «элемент системы» выражены одно через другое и часто условны: то, что является системой для решения одних задач, для других принимается элементом в зависимости от целей изучения, требуемой точности, уровня знаний о надежности и т.д. С точки зрения надежности все технические системы делятся на два вида: 1) Невосстанавливаемые элементы и системы, т.е. неремонтируемые в процессе эксплуатации (радиоэлементы, интегральные схемы, часть приборов, аппаратура летательных аппаратов и т.д.) 2) Восстанавливаемые элементы и системы, которые могут быть отремонтированы непосредственно после отказа в заданное время. Само понятие «восстановление» следует понимать не только как корректировку, настройку, пайку или иные ремонтные работы по отношению к тем или иным техническим средствам, но и замену этих средств. Подавляющее большинство систем, применяющихся для автоматизации технологических процессов, как правило, подлежит восстановлению после отказа, после чего они вновь продолжают работу. Работоспособность- такое состояние изделия, при котором оно соответствует всем требованиям, предъявляемым к его основным параметрам. К числу основных параметров технических систем относятся: быстродействие; нагрузочная характеристика; устойчивость и точность выполнения операций. Комплекс других показателей технической системы: масса, габариты, удобство в обслуживании и др. могут изменяться с течением времени. Эти изменения имеют допустимые значения, их превышение может привести к возникновению отказного состояния (частичного или полного). Состояния технической системы могут быть также разделены на: исправное при котором система полностью соответствует всем требованиям нормативно-технической документации и конструкторской документации; неисправное – когда система имеет хотя бы одно несоответствие этим требованиям. Событие, заключающееся в нарушении работоспособности системы, т.е. в переходе ее из работоспособного состояния в неработоспособное состояние, называется отказом. Событие, заключающееся в переходе системы из исправного в неисправное (но работоспособное) состояние, называется повреждением. Предельное состояние – возникает при условии, когда дальнейшее применение технической системы или оборудования невозможно или нецелесообразно. После попадания в предельное состояние может следовать ремонт (капитальный или средний), в результате чего восстанавливается исправное состояние, или же система окончательно прекращает использоваться по назначению (физическое и моральное старение, износ).
Рисунок 1 – Схема основных состояний и событий восстанавливаемой системы
ЛЕКЦИЯ 2 Цель лекции: Ознакомление с основными этапами расчета и показателями надежности невосстанавливаемых систем. Нормальное распределение В отличие от экспоненциального распределения нормальное используется для описания таких систем и особенно их элементов, которые подвержены действию износа. При этом обязательно учитывается функция и плотность распределения наработки до отказа T, t - средняя наработка до отказа. Параметрами нормального распределения являются: m – математическое ожидание случайной величины, T – наработки до отказа (или времени безотказной работы); σ – среднеквадратическое отклонение наработки до отказа T по результатам испытаний систем. Нормальное распределение описывает поведение случайных величин в диапазоне (- ∞, ∞ ), но т.к. наработка до отказа является не отрицательной величиной, чтобы это учесть, то вместо нормального в принципе должно использоваться усеченное нормальное распределение. Область возможных значений случайной величины может быть от 0 до ∞ (0 при t=0). Усеченное нормальное распределение применят, если m < 3σ, в противном случае использование более простого нормального (не усеченного) распределения дает достаточную точность. Показатели надежности нормального распределения:
   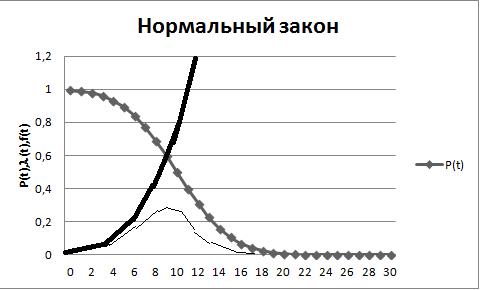
Рисунок 3.2 - Графики изменения показателей надежности при нормальном распределении Лекция 4 Цель лекции: обучение методам расчета показателей надежности восстанавливаемых систем. Лекция 5
Цель лекции: Изучение методов расчета надежности невосстанавливаемых систем при различных сложностях структурной схемы расчета надежности.
5.1 Методы расчета надежности невосстанавливаемых систем
При расчете вероятности безотказной работы, средней наработки до первого отказа элементы системы рассматриваются как невосстанавливаемые. В этом случае при основном (последовательном) соединении элементов (рисунок 5.1) вероятность безотказной работы вычисляется как произведение вероятностей всех элементов: Pс(t) = Р1(t) Р2(t)....Рn-1(t) Рn(t)=
Рисунок 5.1 – Структурная схема расчета надежности, последовательное соединение элементов
При резервном (параллельном) соединении элементов (рисунок 5.2) и при условии, что для работы системы достаточно работы одного из включенных параллельно элементов, отказ системы является совместным событием, имеющим место при отказе всех параллельно включенных элементов. Если параллельно включено элементов и вероятность отказа каждого, то вероятность отказа этой системы: Qc(t) = Q1(t) Q2(t)....Qm-1(t) Qm(t)=
Рисунок 5.2 – Структурная схема расчета надежности, параллельное соединение элементов Если структурная схема надежности состоит из последовательно-параллельного соединения, то расчет надежности использует формулы (5.1) и (5.2). Например, на рисунке 5.3 представлена схема, а уравнение 5.3 демонстрирует расчет функции надежности для этой схемы.
Рисунок 5.3 – Структурная схема расчета надежности, смешанное соединение элементов
Pc(t)= P1(t)*P2(t)*P3456(t) = P1(t)*P2(t)*{1-[1-P3(t)*P4(t)][1-P5(t)*P6(t)]} (5.3) Однако, не все структурные схемы расчета надежности могут быть сведены к последовательно-параллельному соединению. На рисунке 5.4 представлена одинарная мостиковая схема расчета надежности.
Рисунок 5.4 – Мостиковая схема соединения элементов Для всех элементов схемы известны вероятности безотказной работы Р1, Р2, Р3, Р4, Р5 и соответствующие им вероятности отказа типа «обрыв» q1, q2, q3, q4, q5. Необходимо определить вероятность наличия цепи между точками a и b схемы 5.4. Метод перебора состояний Расчету надежности любой системы независимо от используемого метода предшествует определение двух непересекающихся множеств состояний элементов, соответствующих работоспособному и неработоспособному состояниям системы. Каждое из этих состояний характеризуется набором элементов, находящихся в работоспособном и неработоспособном состояниях. Поскольку при независимых отказах вероятность каждого из состояний определяется произведением вероятностей нахождения элементов в соответствующих состояниях, то при числе состояний, равном m, вероятность работоспособного состояния системы определяется выражением:
P =
Вероятность отказа: Q = 1-
где m – общее число работоспособных состояний, в каждом j-м из которых число исправных элементов равно При сравнительно простой структуре системы применение метода перебора состояний сопряжено с громоздкими выкладками. Например, для схемы на рисунке 5.4 составим таблицу состояний, переводя сначала по одному, затем по два, по три элемента в неработоспособное состояние, сохраняя работоспособное состояние системы. Т а б л и ц а 5.1
Если все элементы системы равнонадежны, то вероятность безотказной работы системы при pi=0, 9: Рс= Лекция 6
Цель лекции: Изучение основных способов повышения надежности за счет резервирования. Виды резервирования Для повышения надежности систем и элементов применяют резервирование, основанное на использовании того или иного вида избыточности. Избыточность определяет следующие разновидности резервирования: функциональное, временное, информационное, структурное. В этом случае, если различные системы или устройства выполняют близкие функции, осуществляется функциональное резервирование. Такое резервирование часто применяют для многофункциональных систем. Например, значение температуры пара на выходе котлоагрегата может быть определено по показаниям потенциометра, осуществляющего в комплекте с термоэлектрическим преобразователем индивидуальный контроль ответственного параметра, и с помощью вызова этого параметра на электронное табло информационно-измерительной системы, осуществляющей расчет технико-экономических и других показателей. Временное резервирование заключается в том, что допускается перерыв функционирования системы или устройства из-за отказа элемента. Во многих случаях временное резервирование, обеспечивающее непрерывность технологического процесса, осуществляется за счет введения аккумулирующих емкостей, складов сырья и полуфабрикатов. Например, кратковременный перерыв в подаче топлива не приведет к прекращению генерации пара из-за аккумуляции теплоты поверхностям нагрева котлоагрегата. Информационное резервированиесвязано с возможностью компенсации потери информации по одному каналу информацией по другому каналу. На большинстве технологических объектов, благодаря внутренним связям имеет место информационная избыточность, которая часто используется для оценки достоверности информации. Например, усредненный расход пара на выходе котла соответствует усредненному расходу воды на его выходе, расход газа на котле определяет расход воздуха при фиксированном составе дымовых газов. Для локальных систем наиболее характерно структурное резервирование.При этом виде резервирования повышение надежности достигается путем введения дополнительных элементов в структуру системы.
Структурное резервирование
Структурное резервирование разделяют на общее и поэлементное (раздельное). При общем резервировании система или устройство резервируется в целом, при поэлементном резервируются отдельные элементы или их группы. Если резервные элементы функционируют наравне с основными элементами, то имеет место постоянное резервирование, являющееся пассивным. Если резерв вводится в состав системы после отказа основного элемента и сопровождается переключающимися операциями, то имеет место резервирование замещением – активное резервирование. Схемы общего постоянного (а) и общего резервирования замещением (б) приведены на рисунке 6.1.
а) б)
Рисунок 6.1 - Схемы общего резервирования
При поэлементном способе резервирования (рисунок 6.2 а- постоянном, б - замещением) резервные элементы могут находиться в нагруженном, облегченном и ненагруженном состоянии. При нагруженном (горячем) резерве интенсивность отказов основного При ненагруженном (холодном) резерве вероятностью отказов элементов в состоянии резерва можно пренебречь,
а) б)
Рисунок 6.2 – Схемы поэлементного резервирования
При резервировании замещением один и тот же резерв может быть использован для замены любого из ряда однотипных элементов. Такой способ резервирования называют скользящим или с неоднозначным соответствием. В подсистемах автоматизированных систем управления широко используются все рассмотренные способы резервирования. В локальных системах в основном применяют поэлементное (рисунок 6.2, б) резервирование замещением с ненагруженным резервом. Отказавшие первичные и вторичные приборы, регулирующие блоки и блоки управления, исполнительные механизмы заменяют исправными (со склада). Для характеристики соотношения между общим числом однотипных элементов n и числом r необходимых для функционирования системы работающих элементов вводится понятие кратности резервирования
k = (n - r)/r. (6.1)
Значение k может быть целым, если r =1, и дробным, если r > 1. В этом случае дробь нельзя сокращать. Скользящее резервирование является разновидностью резервирования с дробной кратностью. Структурное резервирование сопряжено с дополнительными затратами на резервные элементы, то они должны окупаться за счет повышения надежности системы и снижения потерь от ее отказов. Наиболее простыми показателями эффективности резервирования является следующее выражение:
Вτ = τ р /τ; Вр = Рр/Р; ВQ = Q/Qр (6.2)
где Вτ – выигрыш за счет повышения средней наработки до отказа резервированной системы τ р по сравнению с наработкой нерезервированной системы τ; Вр и ВQ – аналогичные показатели по повышению вероятности безотказной работы и снижению вероятности отказа. Резервирование эффективно, если значение показателей Вр, ВQ и Вτ больше единицы.
Лекция 7
Цель лекции: обучение методам расчета надежности невосстанавливаемых систем с постоянным резервом
Поэлементное резервирование Надежность системы, содержащей группы элементов или отдельные элементы с поэлементным резервированием (рисунок 7.3, б), рассчитываются с использованием формул общего постоянного резервирования (5.1) и (5.2). Так, если система состоит из n участков с поэлементным резервированием целой кратностью ki, то вероятность безотказной работы системы:
где qij – вероятность отказа j–го элемента, входящего в i–й участок резервирования. Для сопоставления эффективности общего и поэлементного резервирования сравним вероятности отказа двух систем, включающих одинаковое n(k+1) число равнонадежных элементов. Вероятность отказа системы с общим резервированием:
Считая, что вероятность отказа каждого из элементов q< < 1 (1-q)n≈ 1-nq, Qop=nk+1qk+1. Для раздельного резервирования, используя (7.3) и считая q< < 1, получаем: Qпр=1-(1-qk+1)n≈ nqk+1. Эффективность поэлементного резервирования по сравнению с общим Qop/Qпр составит nk. С увеличением глубины n и кратности k резервирования его эффективность растет. Использование поэлементного резервирования сопряжено с введением дополнительных подключающих элементов, имеющих ограниченную надежность. В связи с этим имеется оптимальная глубина резервирования nопт, при n> nопт эффективность резервирования снижается.
Лекция 8 Цель лекции: Обучение основным методам расчета надежности восстанавливаемых систем в процессе эксплуатации. Лекция 9
Цель лекции: Обучение основных практических методов оценки надежности по результатам испытаний. Определительные испытания
Определительным испытаниям могут подвергаться автоматизированные системы управления в целом, их подсистемы, функции, технические средства и любые другие элементы систем. Перед началом определительных испытаний составляется план испытаний. Планом испытаний называют правила, устанавливающие объем выборки, порядок их проведения испытаний и критерии их прекращения. Рассмотрим наиболее распространенные планы определительных испытаний. Наименование плана принято обозначать тремя буквами (цифрами): первая из них обозначает число испытуемых систем, вторая – наличие R или отсутствие U восстановлений на время испытаний в случае отказа, третья – критерий прекращения испытаний. План [NUŤ ] соответствует одновременному испытанию систем. Эти системы после отказа не восстанавливаются (или же восстанавливаются, но данные о их поведении после первого отказа в испытаниях не рассматриваются). Испытания прекращают по истечении наработки каждой отказавшей системы. На рисунке 9.1, а знаком «х» обозначено наличие отказа; ti - наработка до отказа i–ой системы. Этот план обычно применяют для определения вероятности безотказной работы системы за время Ť.
а) б)
в) г) Рисунок 9.1 – Планы испытаний Испытания прекращают по истечении наработки каждой отказавшей системы. Этот план обычно применяют для определения вероятности безотказной работы системы за указанное время Ť. План [NUr]– соответствует испытаниям N таких же невосстанавливаемых систем, однако в отличие от плана[NUT] испытание прекращают, когда число отказавщих систем достигает r. На рисунке 9.1, б, r -ый отказ имеет место у i–ой системы. Если r = N, переходим к плану [NUN], когда испытания прекращаются после отказов всех систем. План [NUr] обычно применяют для определения средней наработки до отказа в случае экспоненциального распределения, а план [NUN] – в случае нормального распределения. Испытания по плану [NUN] требуют значительных времени и числа испытываемых систем, но дают возможность полностью определить эмпирическую функцию распределения. Планы [NUr], [NUŤ ] позволяют определить эмпирическую функцию распределения только для некоторого интервала времени, дают меньше информации, зато позволяют быстрее закончить испытания. План [NRŤ ]– описывает испытания N систем причем отказавшие во время испытаний системы заменяют новым или восстанавливают. Испытания прекращают по истечении наработки Ť каждой из позиций (под позицией понимаем определенное место на стенде или объекте, применительно к которому наработка исчисляется независимо от произошедших на данной позиции замен или восстановлений – рисунок 9.1, в) План [NRr] – соответствует испытанияv N систем, когда отказавшие во время испытаний системы заменяют новыми или восстанавливают. Испытание прекращают, когда суммарное по всем позициям число отказавших систем достигает r (рисунок 9.1, г). Задачами планирования является определение минимального объема наблюдений – выбор числа испытываемых систем N, а также продолжительности наблюдений Ť для планов [NUŤ ] и [NRŤ ]или числа отказов r для планов [NUr] и [NRr]. Результатами определительных испытаний должны являться точечные и интервальные оценки показателей надежности. Точечная оценка понятие математической статистики. Пусть имеются результаты k наблюдений t1, t2, ….tk над некоторой случайной величиной Т с функцией распределения F(t, υ ), причем праметр υ этого распределения неизвестен. Необходимо найти такую функцию ῦ =g(t1, t2, ….tk) результатов наблюдений t1, ….tk, которую можно было рассматривать как оценку параметра υ. При таком выборе финкций g каждой совокупности (t1, ….tk) будет соответствовать точка ῦ на числововй оси, которую называют точечной оценкой параметра υ. Статистические определения показателей надежности, приведенные в лекции 2, являются их точечными оценками. При этом оценка средней наработки до отказа, соответствует плану [NUN], так как здесь рассматриваются завершенные (не прерванные в испытаниях) наработки до отказа каждой из испытуемых систем.
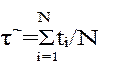
Это соотношение имеет место при любых законах распределения наработки до отказа. Для экспоненциального распределения, кроме плана [NUN] , точечная оценка средней наработки до отказа:

где S - суммарная наработка всех систем за время испытаний; nS - суммарное число отказов всех систем на время испытаний. Например, при плане [NUŤ ]

где L - число систем, отказавших на интервале (0, Ť ); ti - наработка до отказа i– той системы из числа отказавших (i=1, L). При плане [NUr]

Оценка интенсивности отказов λ ˜ при экспоненциальном распределении согласно (3.6) может быть определена через оценку средней наработки до отказа:
 совпадает с оценкой интенсивности отказов совпадает с оценкой интенсивности отказов 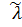 : :
При нормальном распределении и плане [NUN]:

Величину VН называют нижней доверительной границей параметра V при односторонней доверительной вероятности γ 1. Для заданной вероятности γ 2 по той же совокупности наблюдений может быть найдена функция Vвр = gвр(t1, t2…, tk) такая, что интервал (0, Vвр) накрывает параметр V с вероятностью γ 2:

Величину VВР называют верхней доверительной границей параметра V при односторонней доверительной вероятности γ 2. Нижняя и верхняя доверительные границы образуют доверительный интервал, который с вероятностью γ накрывает на числовой оси неизвестное значение параметра V. При γ 1> 0, 5 и γ 2> 0, 5 (доверительные вероятности γ 1 и γ 2 обычно выбираются не менее 0, 8) согласно (9.8) и (9.9):
где γ = γ 1 + γ 2 -1; Обычно принимают, что γ 1 = γ 2, тогда γ = 2 γ 1 – 1. Значение доверительного интервала тем меньше. Чем больше число наблюдений (например, чем больше число отказов при испытаниях) и чем меньше значение γ доверительной вероятности. Определение границ доверительного интервала заключается в следующем. Так как оценка
Контрольные испытания Контрольным испытаниям обычно подвергаются подсистемы, технические средства и их элементы. Для технических средств обязательными являются контрольные испытания на безотказность. Испытания на ремонтопригодность, сохраняемость и долговечность проводят в тех случаях, когда это предусмотрено стандартами, техническими заданиями или техническими условиями на конкретный прибор (средства). Периодичность контрольных испытаний на безотказность обычно не реже одного раза в три года. Для проведения контрольных испытаний из совокупности (партия) однородных приборов составляется некоторая выборка и проводятся испытания на надежность попавших в эту партию приборов. По результатам испытания выборки выносится суждение о соответствии всей партии предъявленным требованиям. Математический аппарат решения задачи – изучаемые в математической статистике методы проверки статистических гипотез. В качестве проверяемой (или, как принято говорить, нулевой) гипотезы принимается предположение, что партия соответствует требованиям к надежности, в качестве противоположной (альтернативной) – что партия не удовлетворяет этим требованиям. По результатам испытаний имеет место одна из следующих четырех ситуаций: 1. Партия удовлетворяет требованиям; по результатам испытаний подтвердилась нулевая гипотеза и принято решение о принятии партии. Это решение правильно. 2. Партия удовлетворяет требованиям, но по результатам испытаний нулевая гипотеза не подтвердилась. Это произошло потому, что случайно составленная выборка содержала повышенное число отказавших приборов по сравнению с совокупностью. Принята альтернативная гипотеза; это решение неправильно и невыгодно для изготовителя приборов. При этом произошла ошибка, вероятность которой называют риском поставщика (изготовителя) α. 3. Партия не удовлетворяет требованиям, по результатам испытаний нулевая гипотеза не подтвердилась. Принята альтернативная гипотеза, т.е. решение о неприятии партии. Это решение правильно. 4. Партия не удовлетворяет требованиям, но по результатам испытаний подтвердилась нулевая гипотеза о соответствии требованиям надежности, так как выборка содержала повышенное число неотказавших приборов по сравнению со всей партией. Принято решение, но оно не выгодно в отличие от п. 2 не изготовителю, а потребителю – заказчику эти приборов. Произошла ошибка, вероятность которой называют риском потребителя (заказчика) β. Естественно, что желательно снизить значения обеих ошибок, доведя их до нуля. Зависимость вероятности L приемки партии от показателя надежности А ( называемой оперативной характеристикой плана контроля) для такой предельной ситуации дана на рисунке 9.2, а. Пусть Атр – требуемое значение показателя надежности. В этой ситуации нулевая гипотеза А≥ Атр. Если она справедлива, то партия принимается с вероятностью равной единице, причем α =0. Альтернативная гипотеза заключается в том, что А£ Атр. При этом партия бракуется с вероятностью, равной единице, причем β =0.Однако такая идеальная оперативная характеристика недостижима, так как требует бесконечного объема наблюдений. В реальной ситуации вводятся два уровня контролируемого показателя надежности: приемочный Аα и браковочный Аβ (рисунок 9.2, б).
а) б) Рисунок 9.2 – Идеальная (а) и реальная (б) оперативные характеристики планов контроля Если А≥ Аα , то приборы должны приниматься с достаточно высокой вероятностью, не ниже L(Аα ), если А£ Аβ , то приборы должны браковаться с достаточно высокой вероятностью, не ниже 1 – L(Аβ ). При этом риск поставщика α =1-L(Аα ), риск потребителя β =1-L(Аβ ). Тем самым проверку нулевой гипотезы А≥ Атр при альтернативе А£ Атр заменяем другой задачей – проверкой нулевой гипотезы А≥ Аα при альтернативе А£ Аβ . Чем ближе Аα к Аβ , тем больший объем испытаний необходим для принятия достоверного решения о соответствии партии. Значение браковочного уровня Аβ устанавливается с учетом приемочного уровня Аα , стоимости, продолжительности и условий испытаний и т.п. Риск поставщика α и потребителя β обычно принимается равным 0, 1-0, 2, но в принципе по согласованию между потребителем и поставщиком возможен выбор и иных значений α и β. Контрольные испытания на безотказность проводятся обычно одно- или двухступенчатым методом. При применении первого из них испытания выполняют следующим образом. Образцы, вошедшие в выборку объема d, испытывают в течение времени tи. По окончании испытаний определяют число наступивших отказов n. Если оно равно или меньше приемочного числа с, определенного в зависимости от величины Аα , Аβ , α и β, то нулевая гипотеза подтверждается и партию принимают. Если же n> с, то подтверждается альтернативная гипотеза и партию не принимают. Одноступенчатый метод при прочих равных условиях обеспечивает минимальную календарную продолжительность испытаний, двухступенчатый при тех же условиях позволяет обеспечить минимум среднего объема испытаний.
Лекция 10 Цель лекции: Обучение основным методам повышения надежности на этапе проектирования и эксплуатации. Лекция 11 Популярное:
|
Последнее изменение этой страницы: 2016-04-11; Просмотров: 1225; Нарушение авторского права страницы