|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
|
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Несколько независимых переменныхСтр 1 из 5Следующая ⇒
К лабораторной работе № 6
”Многомерный регрессионный анализ в Minitab for Windows и
по дисциплине “ Прогнозирование деятельности предприятия ” для студентов всех форм обучения
Севастополь СОДЕРЖАНИЕ
1 Цель работы.. 3 2 Теоретические сведения. 3 2.1 Несколько независимых переменных. 3 2.2 Корреляционная матрица. 3 2.3 Многомерная регрессионная модель. 4 2.4 Статистический анализ модели многомерной регрессии. 5 2.5 Фиктивные переменные. 9 2.6 Мультиколлинеарность. 9 2.7 Выбор «наилучшего» уравнения регрессии. 10 2.8 Регрессионная диагностика и анализ остатков. 14 3 Практическая часть. 16 3.1 Постановка задачи. 16 3.2 Пример использования Minitab for Windows для построения уравнения регрессии 16 4 Порядок выполнения работы.. 23 5 Контрольные вопросы.. 23 Библиографический список. 24 Приложение А Исходные данные. 25
Цель работы Ознакомиться с основными возможностями применения многомерного регрессионного анализа для прогнозирования данных с использованием Minitab for Windows.
Теоретические сведения Несколько независимых переменных Для точного прогнозирования зависимой переменной часто требуется знать значения более чем одной независимой переменной. Регрессионные модели с более чем одной независимой переменной называются моделями многомерной регрессии. Большинство понятий, введенных для простой линейной регрессии, распространяется и на многомерную регрессию. Новая независимая переменная не должна быть тесно связана с уже использованной независимой переменной. Если две независимые переменные тесно связаны, то они будут объяснять одну и ту же изменчивость, и поэтому добавление второй переменной не позволит улучшить прогнозирование. В таких областях, как эконометрика и прикладная статистика, значительная часть возникающих проблем связана как раз с взаимной корреляцией между независимыми переменными. Подобное состояние обычно называют мультиколлинеарностью. Простое решение проблемы наличия двух тесно связанных независимых переменных состоит в том, чтобы не использовать их вместе. Проблема мультиколлинеарности будет рассмотрена ниже. Таким образом, выделяют следующие признаки независимой переменной: - связана с зависимой переменной; - не имеет тесной связи с любой другой независимой переменной.
Корреляционная матрица Для оценки переменных используют корреляционную матрицу. Корреляционная матрица составляется из коэффициентов корреляции, вычисленных для каждой возможной пары переменных. Пример корреляционной матрицы приведен в табл. 1.
Таблица 1 – Пример корреляционной матрицы
В табл. 1 через r12 обозначен коэффициент корреляции, показывающий взаимосвязь между переменными 1 и 2. Отметим, что первый индекс задает номер строки, а второй – номер столбца таблицы. Такой подход позволяет проанализировать взаимозависимость, существующую между двумя любыми переменными. Безусловно, корреляция, например, между переменными 1 и 2 точно такая же, как и между переменными 2 и 1, а значит r12 = r21. Следовательно, для анализа достаточно рассмотреть только половину корреляционной матрицы. Кроме того, корреляция каждой переменной с самой собой всегда равна 1. Анализ корреляционной матрицы – это первый шаг при решении любой задачи, в которой имеется несколько независимых переменных.
Статистический анализ модели многомерной регрессии Разложение дисперсии Статистический анализ модели многомерной регрессии проводится аналогично анализу простой линейной регрессии. Стандартные пакеты статистических программ позволяют изучить оценки по методу наименьших квадратов для параметров модели, оценки их стандартных ошибок, а также значение t-статистики, используемой для проверки значимости отдельных слагаемых регрессионной модели, и величину F-статистики, служащей для проверки значимости регрессионной зависимости. Вычисление указанных значений вручную при многомерном регрессионном анализе крайне непрактично - подобные вычисления следует проводить только с помощью компьютера.
является прогнозом, вычисленным по найденному уравнению регрессии. Форма разбиения суммы квадратов и соответствующие степени свободы здесь следующие:
Общая вариация зависимой переменной, SST, состоит из двух компонент: SSR, вариации, объясненной независимыми переменными через функцию регрессии, и SSE, необъясненной вариации. Информация из уравнения может быть получена в таблице анализа дисперсии ANOVA.
Значимость регрессии Таблица анализа дисперсии ANOVA строится на разложении общей вариации Y (SST) на объясненную (SSR) и необъясненную (SSE) части. Общий ее вид приведен в табл. 2.
Таблица 2 - Таблица анализа дисперсии ANOVA
Рассмотрим гипотезу В простой линейной регрессии имеется лишь одна независимая переменная. Поэтому для нее проверка значимости регрессии, использующая величину отношения F из таблицы ANOVA, эквивалентна двухстороннему t-критерию проверки гипотезы о равенстве нулю углового коэффициента. Для многомерной регрессии t-критерий проверяет значимость каждой отдельной переменной X в функции регрессии, а F-критерий — значимость всех переменных X вместе. При уровне значимости Коэффициент детерминации
Коэффициент детерминации Значение Величина Для многомерной регрессии:
поэтому, при прочих равных показателях, значимые регрессионные зависимости соответствуют сравнительно большим значениям
Фиктивные переменные Иногда требуется определить, как зависимая переменная связана с независимой, когда на ситуацию дополнительно влияет некоторый качественный фактор. Эта зависимость отображается в создании фиктивной переменной. Существует много способов связать классы качественной переменной с количественными величинами. Фиктивные, или индикаторные, переменные используются для определения взаимосвязи между качественными независимыми переменными и зависимой переменной.
Мультиколлинеарность Во многих случаях применения методов регрессии в качестве данных просто используются все доступные значения предварительно назначенных независимых переменных. В подобных ситуациях независимые переменные часто оказываются линейно зависимыми. Если линейная зависимость не точная, для оценки коэффициентов регрессии может по-прежнему применяться метод наименьших квадратов. Однако в этом случае полученные оценки часто характеризуются неустойчивостью (значения коэффициентов могут существенно изменяться даже при относительно небольших изменениях данных) и определенной избыточностью (рассчитанные величины, как правило, оказываются больше ожидаемых). В частности, отдельные коэффициенты могут иметь неверный знак, а значения t-статистики для отдельных слагаемых могут все оказаться незначимыми, в то время как F-тест демонстрирует значимость регрессии. К тому же вычисления по методу наименьших квадратов могут оказаться чувствительными к ошибкам округления. Линейная зависимость между двумя или более независимыми переменными называется мультиколлинеарностью. Степень мультиколлинеарности измеряется фактором роста дисперсии (VIF):
где Если j-я независимая переменная не связана с остальными X, то Для оценки эффекта одной, отдельно взятой независимой переменной при наличии в модели мультиколлинеарности существует несколько способов, ни один из которых не является универсальным для всех возможных случаев. 1 Создать новые переменные X, которые обозначим как
Все новые переменные будут иметь нулевое среднее значение и одно и то же выборочное среднеквадратическое отклонение. Вычисления коэффициентов регрессии для этих новых независимых переменных будут менее чувствительны к ошибкам округления при наличии мультиколлинеарности. 2 Найти и удалить из набора данных одну или более независимых переменных, являющихся избыточными. 3 Воспользоваться методом оценки, отличным от метода наименьших квадратов. 4 Представить зависимую переменную Y как линейную комбинацию некоррелирующих между собой независимых переменных Х. 5 Отобрать независимые переменные на начальном этапе исследования (сразу отказываться от переменных, " говорящих об одном и том же" ).
Пошаговая регрессия Процедура пошаговой регрессии предусматривает поэтапное добавление в уравнение отдельных независимых переменных, по одной переменной на каждом этапе. При использовании этой процедуры компьютер позволяет обработать большое количество независимых переменных за одно выполнение программы. Пошаговая регрессия наилучшим образом может быть описана посредством перечисления основных этапов проводимых вычислений (алгоритмом): 1 Рассматриваются все возможные простые регрессии. Независимая переменная, объясняющая наибольшую значимую долю вариации Y (имеет наибольшую корреляцию с зависимой переменной), - это первая переменная, включаемая в уравнение регрессии. 2 Следующая переменная, вводимая в уравнение, - это та (из еще не включенных в уравнение), которая привносит наибольший значимый вклад в регрессионную сумму квадратов. Является ли этот вклад значимым, определяется с помощью F-теста. Значение F-статистики, которое должно быть превышено для признания значимости некоторой переменной, часто называется значением F для включения. 3 После включения дополнительной переменной в уравнение, отдельный вклад в регрессионную сумму квадратов каждой из переменных, уже включенных в уравнение, проверяется на значимость с помощью F-теста. Если полученное значение F-статистики окажется меньше, чем величина, называемая F для исключения, данная переменная исключается из уравнения регрессии. 4 Этапы 2 и 3 повторяются, пока все возможные добавления не окажутся незначимыми, а все возможные удаления - значимыми. В этот момент процедура выбора заканчивается. Пошаговая регрессия позволяет включать или исключать независимые переменные из уравнения регрессии на разных этапах исследования. Независимая переменная удаляется из модели, если она перестает давать значимый вклад при добавлении новой переменной. Пользователь программы пошаговой регрессии сам указывает значения, определяющие, остается ли переменная в уравнении или удаляется. Поскольку F-статистика, используемая в пошаговой регрессии, такова, что F=t2, где t – t-статистика для проверки значимости независимой переменной, F = 4 (соответствующее |t|=2) - это обычный выбор значения F для включения и F для исключения. Значение F для включения, равное 4, по существу, эквивалентно проверке на значимость независимой переменной на уровне 5%. Программа пошаговой регрессии в приложении Minitab предусматривает, что пользователь выбирает уровень Результат пошаговой процедуры - это регрессионная модель, содержащая только независимые переменные с величинами t, значимыми на указанном уровне. Однако поскольку процедура проводилась шаг за шагом, у нас нет гарантии, что в данную регрессию включены, к примеру, три наилучшие для составления прогноза переменные. Кроме того, метод автоматического отбора не позволяет указать на необходимость преобразования переменных и исключить проблему мультиколлинеарности. Наконец, пошаговая регрессия не может создать важные переменные, не указанные пользователем. В любом случае необходимо тщательно продумать набор независимых переменных, предлагаемых для исследования с помощью программы пошаговой регрессии. Метод пошаговой регрессии очень прост и удобен в использовании. К несчастью, этот метод можно очень легко употребить неправильно. Зачастую, изучая модель регрессии, исследователь создает большое количество возможных независимых переменных, а затем с помощью пошаговой процедуры определяет, какие из них являются значимыми. Проблема заключается в том, что при анализе большого количества независимых переменных проводится очень много t-тестов и становится вполне возможным допустить ошибку I рода (добавить незначимую переменную). В этом случае окончательная модель будет содержать переменную, не связанную с зависимой переменной линейно и включенную в модель только по случайности. Как было отмечено выше, еще одна проблема связана с исходным выбором возможных независимых переменных. Когда эти переменные отобраны, слагаемые высших порядков (криволинейные, нелинейные и произведения) часто пропускаются с тем, чтобы сохранить лишь переменные, удобные для исследования. Таким образом, несколько важных переменных могут быть исключены из модели изначально. Становится очевидным, что интуитивный выбор исследователем начального множества независимых переменных – весьма критический момент в получении удачной регрессионной модели.
Практическая часть Постановка задачи Осуществить прогнозирование данных с использованием регрессионного анализа в системе Minitab for Windows и приложении MS Excel.
Таблица 3 Исходные данные для проведения анализа
Пример использования Minitab for Windows для построения уравнения регрессии 1 Ввести данные в Minitab for Windows 2 Для проведения корреляционного анализа выбрать команду Startà Basic Statisticà Correlation 3 На экране раскроется диалоговое окно Correlation (Корреляция), представленное на рис. 1
Рис. 1. Диалоговое окно Correlation приложения Minitab
а) в поле Variables ввести значения Y, X1, X2, X3, X4, X5. б) щелкнуть на кнопке ОК, и на экран будут выведены результаты, представленные в листинге (рис. 2).
Рис.2 Листинг результата корреляционного анализа в системе Minitab
Корреляционная матрица показывает наличие достаточно тесной связи между зависимой переменной Y и независимыми переменными. 4 Для запуска процедуры анализа регрессии выбрать команду Startà Regressionà Regression 3 На экране раскроется диалоговое окно Regression (регрессия) а) в поле Response в качестве зависимой переменной выбрать величину Y б) в поле Predictors в качестве независимых переменных выбрать величины X1, X2, X3, X4, X5 в) для продолжения работы щелкнуть на кнопке Options. В появившемся окне выбрать Variance inflation factor для расчета степени мультиколлинеарности (фактор роста дисперсии (VIF)). г) щелкнуть на кнопке ОК, и на экран будут выведены результаты, представленные в листинге (рис. 3).
Рис.3. Листинг результатов регрессионного анализа
Ниже объясняется используемая в приложении Minitab терминология, даются необходимые определения и описываются выполняемые вычисления. Все эти пояснения относятся к содержимому листинга, представленного на рис. 3. - Coef - коэффициенты регрессии. Найденное уравнение регрессии является следующим:
Y = - 89, 7 + 0, 202 X1 + 6, 12 X2 + 0, 113 X3 - 0, 005 X4 - 0, 50 X5
- R-Sq - уравнение регрессии объясняет 89, 5% вариации объема продаж. - s - стандартная ошибка оценки равна 3, 97 ед.. Эта величина является мерой отклонения полученных значений от величин прогноза. - Т – значение t-статистики. В этом случае большое значение статистики для переменных X1, X2, и малое значение р указывают, что коэффициент при этих переменных значимо отличаются от нуля. Таким образом, коэффициенты при обеих независимых переменных значимо отличаются от нуля. - Р - значение р = 0, 000 равно вероятности получить значение t с абсолютной величиной, не меньшей 7, 20, если гипотеза - SS - разложение суммы квадратов, SST=SSR + SSE (общая сумма квадратов = сумма квадратов регрессии + сумма квадратов ошибок). - F - вычисленное значение F (41, 10) используется для проверки значимости регрессии. Табличное значение F-статистики с числом степеней свободы df=5, 24 при уровне значимости 5% равно 2, 62. Следовательно, регрессия значима. Функция регрессии объясняет значительную часть изменчивости Y. - R-Sq(adj) - скорректированный коэффициент детерминации. - Значение VIF для переменных Х2 и Х5 говорит о наличии мультиколлинеарности. Последовательно избавляясь от незначимых переменных в уравнении регрессии (повторяя шаг 3 для оставшихся переменных) получим итоговое уравнение (листинг представлен на рис. 4)
Рис.4 Листинг результатов регрессионного анализа (итоговый)
Таким образом, полученное уравнение регрессии объясняет 89, 5% вариации параметра Y. Мультиколлинеарность переменных отсутствует. По t-статистике коэффициенты уравнения регрессии значимы, по F-статистике уравнение также значимо. 5 Чтобы получить графики остатков, выбрать команду Stats à Regression à Residual plots. Графики остатков представлены на рисунке 5.
    
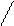
Рис.5 Графики остатков
Анализ графиков также свидетельствует, что уравнение регрессии адекватно описывает взаимосвязь между объемами продаж за месяц (Y), результатами теста способностей (X1) и возрастом продавцов (X2). Рост результатов теста способностей на единицу приводит к росту объема продаж на 0, 2 единицы, увеличение возраста исполнителя на единицу (внутри исследуемого интервала значений Х2) приводит к росту объема продаж на 5, 93 единицы. 6 Результат автокорреляционного анализа остатков представлен на рис. 6 Так как все значения автокорреляции близки к нулю и находятся в доверительном интервале, можно сделать вывод о случайности (независимости) остатков. Следовательно, уравнение регрессии можно использовать для интерпретации имеющихся данных. 7 Для определения прогнозного объема продаж необходимо подставить требуемые значения в уравнение регрессии:
Y = - 86, 8 + 0, 200 X1 + 5, 93 X2 =-86, 8+0, 200*83+5, 93*25 = 78, 05 ед.
Рис.6 Автокорреляционный анализ остатков
Т.е. при найме на работу сотрудника прошедшего тест на способности на 83 балла возрастом 25 лет, можно ожидать, что ежемесячный объем продаж составит 78, 05 ед. Интервальный прогноз можно получить, воспользовавшись теоретическими положениями, изложенными в п. 2.4.5. 7 Для запуска процедуры пошаговой регрессии выбрать команду Statà Regressionà Stepwise. 8 На экране появится диалоговое окно Stepwise Regression, показанное на рис. 7
Puc. 7 Диалоговое окно Stepwise Regression приложения Minitab
а) зависимая переменная (Response) содержится в столбце С1, озаглавленном Y; б) независимые переменные содержатся в столбцах С2-С6, озаглавленных X1, X2, X3, X4, X5 в) чтобы ввести значение уровня значимости, щелкнуть на кнопке Methods 9 На экране раскроется диалоговое окно Stepwise-Methods, показанное на рис. 8.
Рис. 8. Диалоговое окно Stepwise-Method приложения Minitab
а) поскольку в расчетах используется уровень значимости 0, 05, изменить значения в полях Alpha to enter и Alpha to remove с 0, 15 на 0, 05 б) щелкнуть на кнопке ОК, а затем еще раз на кнопке ОК в диалоговом окне Stepwise Regression. На экран будут выведены результаты, представленные на рис. 9.
Рис. 9 Листинг результатов пошаговой регрессии в приложении Minitab
По рис. 9 видно, что переменная возраста вводится в уравнение регрессии первой и объясняет 63, 7% дисперсии значений объема продаж. Поскольку значение р, равное 0, 0000, меньше величины Следовательно, уравнение регрессии примет вид:
Y = - 86, 8 + 5, 93 X2 + 0, 200 X1
Порядок выполнения работы 1 Изучить методические указания к выполнению работы. 2 Провести анализ данных с использованием Minitab for Windows. Исходные данные представлены в приложении А. 3 Подготовить отчет по лабораторной работе. 4Ответить на контрольные вопросы. 5 Защитить лабораторную работу. 5 Контрольные вопросы 1. Каковы характеристики хорошей независимой переменной? 2. Какие предположения связаны с моделью многомерной регрессии? 3. Что измеряет в многомерной регрессии частный или чистый коэффициент? 4. Что измеряет в многомерной регрессии стандартная ошибка оценки? 5. Объясните каждое из следующих понятий: корреляционная матрица, мультиколлинеарность, фиктивная переменная, остатки, пошаговая регрессия? 6. Как рассчитывается коэффициент детерминации и что он характеризует? 7. В чем заключается анализ всех возможных регрессий? В чем его сложность? 8. Какие существуют критерии для выбора уравнения регрессии? Библиографический список
1 Вишнев С.М. Основы комплексного прогнозирования. - М.: Наука, 1997, -287с. 2 Економічний словник-довідник / За ред. д. економ, наук, проф. С.В.Мочерного. - К.: Феміна, 1995.- 368 с. 3 Емельянов А.С.Эконометрия и прогнозирование.- М.: Экономика, 1985.-208с. 4 Тейл Г. Прикладное экономическое прогнозирование: Пер. с англ.-М.: Прогресс, 1970.-504 с. 5 Тейл Г. Экономические прогнозы и принятие решений. Пер. с англ.- М.: Статистика. 1971.- 485 с. 6 Ханк Д.Э. Бизнес прогнозирование // Д.Э. Ханк, Д.У. Уичерн, А.Дж. Райтс. – М.: Издательский дом «Вильямс», 2003. – 656 с.
Приложение А
Популярное:
|
Последнее изменение этой страницы: 2016-05-03; Просмотров: 2197; Нарушение авторского права страницы
. Справедливость этой гипотезы означает, что величина Y не связана ни с какой из переменных X (коэффициент при каждой переменной X, равен нулю). Проверка гипотезы 
фактически является проверкой значимости регрессии. Если регрессионная модель справедлива и гипотеза 
гипотеза 
(расчетное значение F больше значения F-распределения при уровне значимости 
).
вычисляется по формуле: 
для простой линейной регрессии. Он представляет собой долю вариации зависимой переменной Y, которая объясняется взаимосвязью Y с переменными X.
, а это означает, что SSR = 0, и никакая часть вариации величины Y не объясняется регрессией. На практике значение 
называется многомерным коэффициентом корреляции и характеризует корреляцию между зависимой переменной Y и прогнозом. Поскольку 
прогнозирует значение зависимой переменной, значение R всегда неотрицательно и лежит в диапазоне 0 < R < 1.
- коэффициент детерминации из регрессии j-й независимой переменной по оставшимся (k-1) независимым переменным. Для k=2 независимых переменных это значение равно 
(квадрату их выборочного коэффициента корреляции).
и 
. Если зависимость имеет место, то 
. Значение 
, близкое к 1, говорит о том, что для этой переменной проблемы мультиколлинеарности не существует. Оценка ее коэффициента и значение t-статистики не изменятся значительно, если другие независимые переменные будут добавлены в уравнение регрессии или удалены из него. Значение 
, посредством масштабирования всех независимых переменных по следующей формуле: 
справедлива. Поскольку эта вероятность весьма мала, то гипотеза 
отклоняется. Коэффициент при переменных X1, X2 значимо отличны от нуля. Коэффициенты же при переменных X3, X4, X5 незначимы
, переменная возраста добавляется в модель. На втором этапе в уравнение регрессии вводится переменная, характеризующая результаты теста способностей. В этом случае уравнение регрессии объясняет 89, 48% вариации продаж. Коэффициенты регрессий при переменных значительно отличаются от нуля, и вероятность того, что это происходит лишь в результате случайного отклонения почти нулевая.