|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
|
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Регрессионная диагностика и анализ остатков ⇐ ПредыдущаяСтр 5 из 5
Регрессионный анализ будет неполон, пока мы не убедимся, что выбранная модель адекватно представляет данные. Непременно следует проверить адекватность найденной модели до того, как она станет частью методики принятия решений. Исследование остатков - это важный момент в определении адекватности модели. Несколько графиков остатков, строящихся для проверки предположений о модели регрессии, были предложены в Методических указаниях к проведению лабораторной работы №5. Кроме того, если модели регрессии используются с данными временных рядов, важно вычислить автокорреляции остатков для проверки условия их независимости. Выводы (и решения), сделанные по моделям, не соответствующим основным регрессионным предположениям, могут оказаться совершенно ошибочными. Например, можно заключить, что какие-то изменения независимой переменной приведут к нужным изменениям зависимой переменной, что на самом деле окажется не так. Может быть сделан вывод, что прогноз с большой надежностью (с доверительной вероятностью 0, 95) будет не более чем на 2% отличаться от будущего значения зависимой переменной, тогда как фактически доверительная вероятность окажется намного меньше, и т.д. Рассмотрим некоторые дополнительные способы оценки регрессионной модели. Эти способы направлены на выделение наблюдений, крайних в наборе или представляющих собой выбросы (т.е. наблюдений, заметно отличающихся по значению от остальных данных). Выбросы часто скрываются процессом подгонки и не могут быть достаточно просто определены при исследовании графика остатков. Тем не менее, они могут оказывать существенное влияние на выбор подходящей регрессионной функции. Необходимо тщательно изучать выбросы для того, чтобы принять обоснованное решение, следует ли их оставить в наборе данных или удалить из него. И если их оставлять, то следует определить, как лучше поступить - или влияние выбросов на функцию регрессии должно быть уменьшено, или функция регрессии должна быть подправлена. Мера влияния i-й точки данных на положение функции регрессии измеряется значением рычага
Для k независимых переменных выражение для i-го рычага сложнее; однако, можно показать, что 0 < Если i-я точка данных имеет большое значение рычага ( Определение выбросов или крайних значений Y основывается на размерах остатков Пакеты программ, подобные приложению Minitab, отмечают флажком точки данных с крайними значениями Y, вычисляя " стандартизованные" остатки и выделяя точки с большими значениями стандартизованных остатков. Один метод стандартизации основан на том, что оценки стандартных отклонений остатков равны:
где
Все стандартизованные остатки имеют дисперсию 1. Стандартизованный остаток считается большим (а значение соответствующей зависимой переменной - крайним), если
Значения Y, соответствующие точкам данных с большими стандартизованными остатками, могут очень сильно повлиять на расположение прямой регрессии.
Практическая часть Постановка задачи Осуществить прогнозирование данных с использованием регрессионного анализа в системе Minitab for Windows и приложении MS Excel.
Таблица 3 Исходные данные для проведения анализа
Пример использования Minitab for Windows для построения уравнения регрессии 1 Ввести данные в Minitab for Windows 2 Для проведения корреляционного анализа выбрать команду Startà Basic Statisticà Correlation 3 На экране раскроется диалоговое окно Correlation (Корреляция), представленное на рис. 1
Рис. 1. Диалоговое окно Correlation приложения Minitab
а) в поле Variables ввести значения Y, X1, X2, X3, X4, X5. б) щелкнуть на кнопке ОК, и на экран будут выведены результаты, представленные в листинге (рис. 2).
Рис.2 Листинг результата корреляционного анализа в системе Minitab
Корреляционная матрица показывает наличие достаточно тесной связи между зависимой переменной Y и независимыми переменными. 4 Для запуска процедуры анализа регрессии выбрать команду Startà Regressionà Regression 3 На экране раскроется диалоговое окно Regression (регрессия) а) в поле Response в качестве зависимой переменной выбрать величину Y б) в поле Predictors в качестве независимых переменных выбрать величины X1, X2, X3, X4, X5 в) для продолжения работы щелкнуть на кнопке Options. В появившемся окне выбрать Variance inflation factor для расчета степени мультиколлинеарности (фактор роста дисперсии (VIF)). г) щелкнуть на кнопке ОК, и на экран будут выведены результаты, представленные в листинге (рис. 3).
Рис.3. Листинг результатов регрессионного анализа
Ниже объясняется используемая в приложении Minitab терминология, даются необходимые определения и описываются выполняемые вычисления. Все эти пояснения относятся к содержимому листинга, представленного на рис. 3. - Coef - коэффициенты регрессии. Найденное уравнение регрессии является следующим:
Y = - 89, 7 + 0, 202 X1 + 6, 12 X2 + 0, 113 X3 - 0, 005 X4 - 0, 50 X5
- R-Sq - уравнение регрессии объясняет 89, 5% вариации объема продаж. - s - стандартная ошибка оценки равна 3, 97 ед.. Эта величина является мерой отклонения полученных значений от величин прогноза. - Т – значение t-статистики. В этом случае большое значение статистики для переменных X1, X2, и малое значение р указывают, что коэффициент при этих переменных значимо отличаются от нуля. Таким образом, коэффициенты при обеих независимых переменных значимо отличаются от нуля. - Р - значение р = 0, 000 равно вероятности получить значение t с абсолютной величиной, не меньшей 7, 20, если гипотеза - SS - разложение суммы квадратов, SST=SSR + SSE (общая сумма квадратов = сумма квадратов регрессии + сумма квадратов ошибок). - F - вычисленное значение F (41, 10) используется для проверки значимости регрессии. Табличное значение F-статистики с числом степеней свободы df=5, 24 при уровне значимости 5% равно 2, 62. Следовательно, регрессия значима. Функция регрессии объясняет значительную часть изменчивости Y. - R-Sq(adj) - скорректированный коэффициент детерминации. - Значение VIF для переменных Х2 и Х5 говорит о наличии мультиколлинеарности. Последовательно избавляясь от незначимых переменных в уравнении регрессии (повторяя шаг 3 для оставшихся переменных) получим итоговое уравнение (листинг представлен на рис. 4)
Рис.4 Листинг результатов регрессионного анализа (итоговый)
Таким образом, полученное уравнение регрессии объясняет 89, 5% вариации параметра Y. Мультиколлинеарность переменных отсутствует. По t-статистике коэффициенты уравнения регрессии значимы, по F-статистике уравнение также значимо. 5 Чтобы получить графики остатков, выбрать команду Stats à Regression à Residual plots. Графики остатков представлены на рисунке 5.
    
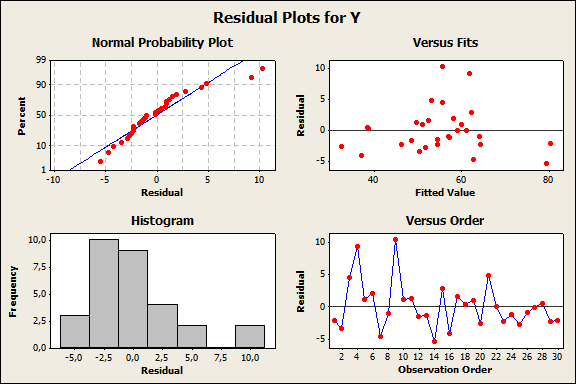
Рис.5 Графики остатков
Анализ графиков также свидетельствует, что уравнение регрессии адекватно описывает взаимосвязь между объемами продаж за месяц (Y), результатами теста способностей (X1) и возрастом продавцов (X2). Рост результатов теста способностей на единицу приводит к росту объема продаж на 0, 2 единицы, увеличение возраста исполнителя на единицу (внутри исследуемого интервала значений Х2) приводит к росту объема продаж на 5, 93 единицы. 6 Результат автокорреляционного анализа остатков представлен на рис. 6 Так как все значения автокорреляции близки к нулю и находятся в доверительном интервале, можно сделать вывод о случайности (независимости) остатков. Следовательно, уравнение регрессии можно использовать для интерпретации имеющихся данных. 7 Для определения прогнозного объема продаж необходимо подставить требуемые значения в уравнение регрессии:
Y = - 86, 8 + 0, 200 X1 + 5, 93 X2 =-86, 8+0, 200*83+5, 93*25 = 78, 05 ед.
Рис.6 Автокорреляционный анализ остатков
Т.е. при найме на работу сотрудника прошедшего тест на способности на 83 балла возрастом 25 лет, можно ожидать, что ежемесячный объем продаж составит 78, 05 ед. Интервальный прогноз можно получить, воспользовавшись теоретическими положениями, изложенными в п. 2.4.5. 7 Для запуска процедуры пошаговой регрессии выбрать команду Statà Regressionà Stepwise. 8 На экране появится диалоговое окно Stepwise Regression, показанное на рис. 7
Puc. 7 Диалоговое окно Stepwise Regression приложения Minitab
а) зависимая переменная (Response) содержится в столбце С1, озаглавленном Y; б) независимые переменные содержатся в столбцах С2-С6, озаглавленных X1, X2, X3, X4, X5 в) чтобы ввести значение уровня значимости, щелкнуть на кнопке Methods 9 На экране раскроется диалоговое окно Stepwise-Methods, показанное на рис. 8.
Рис. 8. Диалоговое окно Stepwise-Method приложения Minitab
а) поскольку в расчетах используется уровень значимости 0, 05, изменить значения в полях Alpha to enter и Alpha to remove с 0, 15 на 0, 05 б) щелкнуть на кнопке ОК, а затем еще раз на кнопке ОК в диалоговом окне Stepwise Regression. На экран будут выведены результаты, представленные на рис. 9.
Рис. 9 Листинг результатов пошаговой регрессии в приложении Minitab
По рис. 9 видно, что переменная возраста вводится в уравнение регрессии первой и объясняет 63, 7% дисперсии значений объема продаж. Поскольку значение р, равное 0, 0000, меньше величины Следовательно, уравнение регрессии примет вид:
Y = - 86, 8 + 5, 93 X2 + 0, 200 X1
Порядок выполнения работы 1 Изучить методические указания к выполнению работы. 2 Провести анализ данных с использованием Minitab for Windows. Исходные данные представлены в приложении А. 3 Подготовить отчет по лабораторной работе. 4Ответить на контрольные вопросы. 5 Защитить лабораторную работу. 5 Контрольные вопросы 1. Каковы характеристики хорошей независимой переменной? 2. Какие предположения связаны с моделью многомерной регрессии? 3. Что измеряет в многомерной регрессии частный или чистый коэффициент? 4. Что измеряет в многомерной регрессии стандартная ошибка оценки? 5. Объясните каждое из следующих понятий: корреляционная матрица, мультиколлинеарность, фиктивная переменная, остатки, пошаговая регрессия? 6. Как рассчитывается коэффициент детерминации и что он характеризует? 7. В чем заключается анализ всех возможных регрессий? В чем его сложность? 8. Какие существуют критерии для выбора уравнения регрессии? Библиографический список
1 Вишнев С.М. Основы комплексного прогнозирования. - М.: Наука, 1997, -287с. 2 Економічний словник-довідник / За ред. д. економ, наук, проф. С.В.Мочерного. - К.: Феміна, 1995.- 368 с. 3 Емельянов А.С.Эконометрия и прогнозирование.- М.: Экономика, 1985.-208с. 4 Тейл Г. Прикладное экономическое прогнозирование: Пер. с англ.-М.: Прогресс, 1970.-504 с. 5 Тейл Г. Экономические прогнозы и принятие решений. Пер. с англ.- М.: Статистика. 1971.- 485 с. 6 Ханк Д.Э. Бизнес прогнозирование // Д.Э. Ханк, Д.У. Уичерн, А.Дж. Райтс. – М.: Издательский дом «Вильямс», 2003. – 656 с.
Приложение А
Популярное:
|
Последнее изменение этой страницы: 2016-05-03; Просмотров: 953; Нарушение авторского права страницы
. Значение рычага зависит только от независимых переменных и не зависит от зависимой переменной Y. Для простой линейной регрессии с одной независимой переменной X: 
.
.
. Большие остатки показывают, что значение Y находится далеко от его прогноза, вычисленного по уравнению регрессии. Большая величина остатка будет выделяться на гистограмме остатков как значение, удаленное от нуля (в любом направлении). На графике зависимости остатков от значений прогноза большой остаток будет выделяться как точка, удаленная вверх или вниз от горизонтальной оси.
- стандартная ошибка оценки, a 
справедлива. Поскольку эта вероятность весьма мала, то гипотеза 
отклоняется. Коэффициент при переменных X1, X2 значимо отличны от нуля. Коэффициенты же при переменных X3, X4, X5 незначимы
, переменная возраста добавляется в модель. На втором этапе в уравнение регрессии вводится переменная, характеризующая результаты теста способностей. В этом случае уравнение регрессии объясняет 89, 48% вариации продаж. Коэффициенты регрессий при переменных значительно отличаются от нуля, и вероятность того, что это происходит лишь в результате случайного отклонения почти нулевая.