Абсолютно и условно сходящиеся несобственные интегралы.

Несобственный интеграл I= 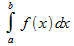называется: а)абсолютно сходящимся, если сходится интеграл = , в этом случае говорят, что ф-ция f абс. интегрируема на промежутке [a; b); б)условно сходящимся, если интеграл I сходится, а расходится.

 

Теорема. Если несобственный интеграл сходится, то интеграл I также сходится и выполняется неравенство: .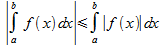

Док-во: 1)Из сходимости следует, что для него выполняется условие Коши, то есть: 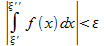. По определению несобственного интеграла I ф-ция f(x) интегрируема по Риману на отрезке с концами и поэтому ф-ция также интегрируема по Риману на этом отрезке. Далее применим правило оценки интегралов и получим: , отсюда следует что f удовлетворяет условию Коши, и по достаточному признаку сходимости сходится интеграл I. 2) - это нер-во справедливо 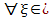[a; b). В силу сходимости I и сущ-ют пределы при 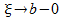левой и правой частей этого нер-ва, равные соответственно I и . Переходим к пределу, получаем .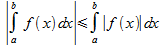

Вопрос 9.

Дифференциа́ льное уравне́ ние — уравнение, связывающее значение производной функции с самой функцией, значениями независимой переменной, числами (параметрами). Порядок входящих в уравнение производных может быть различен (формально он ничем не ограничен). Производные, функции, независимые переменные и параметры могут входить в уравнение в различных комбинациях или все, кроме хотя бы одной производной, отсутствовать вовсе. Дифференциальное уравнение порядка выше первого можно преобразовать в систему уравнений первого порядка, в которой число уравнений равно порядку исходного уравнения.

Теорема существования единственного решения -??

Вопрос 10.

Уравнением с разделенными переменными называется дифференциальное уравнение вида

f(x)dx + g(y)dy = 0

с непрерывными функциями f(х) и g(y).

Равенство

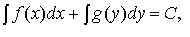
где C — произвольная постоянная, определяет общий интеграл уравнения с разделёнными переменными.

Начальное условие для уравнения f(x)dx + g(y)dy = 0 можно задавать в виде y(x₀) = y₀ или в виде x(y₀) = x₀.

 

Уравнением с разделяющимися переменными называется дифференциальное уравнение вида

f₁(x)g₁ (y)dx + f₂(x) g₂(y)dy =0.

Функции f₁(x), g₁(y), f₂(x), g₂(y) непрерывны в cвоих областях определения и g₁(y)f₂(x) ≠ 0.

 

Разделив обе части уравнения на отличное от нуля произведение g₁(y)f₂(x), получим уравнение с разделенными переменными

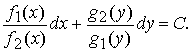
Общий интеграл этого уравнения имеет вид

Вопрос 11.

Линейные дифференциальные уравнения первого порядка

Определение линейного уравнения первого порядка Дифференциальное уравнение вида 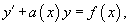где a(x) и b(x) − непрерывные функции x, называтся линейным неоднородным дифференциальным уравнением первого порядка. Мы рассмотрим два метода решения указанных уравнений: Использование интегрирующего множителя; Метод вариации постоянной. Использование интегрирующего множителя Если линейное дифференциальное уравнение записано в стандартной форме: 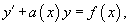то интегрирующий множитель определяется формулой: Умножение левой части уравнения на интегрирующий множитель u(x) преобразует ее в производную произведения y(x)u(x). Общее решение дифференциального уравнения выражается в виде: где C − произвольная постоянная.

Решить уравнение y' − y − xe^x = 0.

Решение.

Запишем данное уравнение в стандартной форме:

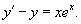
Будем решать это уравнение, используя интегрирующий множитель:

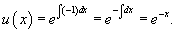
Тогда общее решение линейного дифференциального уравнения определяется выражением:

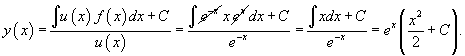
Уравнение Бернулли

Уравнение Бернулли является одним из наиболее известных нелинейных дифференциальных уравнений первого порядка. Оно записывается в виде где a(x) и b(x) − непрерывные функции. Если m = 0, то уравнение Бернулли становится линейным дифференциальным уравнением. В случае когдаm = 1, уравнение преобразуется в уравнение с разделяющимися переменными. В общем случае, когда m ≠ 0, 1, уравнение Бернулли сводится к линейному дифференциальному уравнению с помощью подстановки Новое дифференциальное уравнение для функции z(x) имеет вид и может быть решено способами, описанными на странице Линейные дифференциальные уравнения первого порядка.

Пример 1

Найти общее решение уравнения y' − y = y2ex. Решение. Для заданного уравнения Бернулли m = 2, поэтому сделаем подстановку Дифференцируя обе части уравнения (переменная y при этом рассматривается как сложная функция x), можно записать: Разделим обе части исходного дифференциального уравнения на y2: 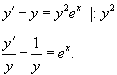Подставляя z и z', находим: 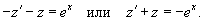Мы получили линейное уравнение для функции z(x). Решим его с помощью интегрирующего множителя: 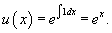Общее решение линейного уравнения выражается формулой Возвращаясь к функции y(x), получаем ответ в неявной форме: который можно записать также в виде: Заметим, что при делении уравнения на y2 мы потеряли решение y = 0. В результате, полный ответ записывается в виде:

Вопрос 13.

	Однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
	Рассмотрим линейное дифференциальное уравнение вида где p, q − постоянные коэффициенты. Для каждого такого дифференциального уравнения можно записать так называемое характеристическое уравнение: Обшее решение однородного дифференциального уравнения зависит от корней характеристического уравнения, которое в данном случае будет являться квадратным уравнением. Возможны следующие случаи: 1. Дискриминант характеристического квадратного уравнения положителен: D > 0. Тогда корни характеристического уравнения k1 и k2 действительны и различны. В этом случае общее решение описывается функцией где C1 и C2 − произвольные действительные числа. 2. Дискриминант характеристического квадратного уравнения равен нулю: D = 0. Тогда корни действительны и равны. В этом случае говорят, что существует один корень k1 второго порядка. Общее решение однородного дифференциального уравнения имеет вид: 3. Дискриминант характеристического квадратного уравнения отрицателен: D < 0. Такое уравнение имеет комплексно-сопряженные корни k1 = α + β i, k1 = α − β i. Общее решение записывается в виде Рассмотренные три случая удобно представить в виде таблицы:
	Пример 1
	Решить дифференциальное уравнение y'' − 6y' + 5y = 0. Решение. Запишем сначала соответствующее характеристическое уравнение: Корни данного уравнения равны k1 = 1, k2 = 5. Поскольку корни действительны и различны, общее решение будет иметь вид: где C1 и C2 − произвольные постоянные.

Вопрос 12. -??

Вопрос 14.

Неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами

Структура общего решения Линейное неоднородное уравнение данного типа имеет вид: 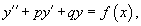где p, q − постоянные числа (которые могут быть как действительными, так и комплексными). Для каждого такого уравнения можно записать соответствующее однородное уравнение: Теорема: Общее решение неоднородного уравнения является суммой общего решения y0(x) соответствуюшего однородного уравнения и частного решения y1(x) неоднородного уравнения: Ниже мы рассмотрим два способа решения неоднородных дифференциальных уравнений. Метод вариации постоянных Если общее решение y0 ассоциированного однородного уравнения известно, то общее решение неоднородного уравнения можно найти, используя метод вариации постоянных. Пусть общее решение однородного дифференциального уравнения второго порядка имеет вид: Вместо постоянных C1 и C2 будем рассматривать вспомогательные функции C1(x) и C2(x). Будем искать эти функции такими, чтобы решение 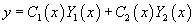удовлетворяло неоднородному уравнению с правой частью f(x). Неизвестные функции C1(x) и C2(x) определяются из системы двух уравнений: Метод неопределенных коэффициентов Правая часть f(x) неоднородного дифференциального уравнения часто представляет собой многочлен, экспоненциальную или тригонометрическую функцию, или некоторую комбинацию указанных функций. В этом случае решение удобнее искать с помощью метода неопределенных коэффициентов. Подчеркнем, что данный метод работает лишь для ограниченного класса функций в правой части, таких как   где Pn(x) и Qm(x) − многочлены степени n и m, соответственно. В обоих случаях выбор частного решения должен соответствовать структуре правой части неоднородного дифференциального уравнения. В случае 1, если число α в экспоненциальной функции совпадает с корнем характеристического уравнения, то частное решение будет содержать дополнительный множитель xs, где s − кратность корня α в характеристическом уравнении. В случае 2, если число α + β i совпадает с корнем характеристического уравнения, то выражение для частного решения будет содержать дополнительный множитель x. Неизвестные коэффициенты можно определить подстановкой найденного выражения для частного решения в исходное неоднородное дифференциальное уравнение. Принцип суперпозиции Если правая часть неоднородного уравнения представляет собой сумму нескольких функций вида то частное решение дифференциального уравнения также будет являться суммой частных решений, построенных отдельно для каждого слагаемого в правой части.

Вопрос 15.

http: //www.bez-dvoek.ru/matem/dif3/dz12.htm

Вопрос 16.

http: //mathhelpplanet.com/static.php? p=sistemy-differentsialnyh-uravnenii

Вопрос 17.

http: //www.pm298.ru/diffur7.php

⇐ Предыдущая123

Поделиться:

Популярное:

1. IV. Прочитайте и перепишите следующие предложения. Определите, к какому типу условного предложения относится каждое из них. Переведите письменно предложение.
2. Абсолютно твердое тело - система материальных точек, расстояние между которыми не изменяются в данной задаче. Абсолютно твердое тело обладает только поступательными и вращательными степенями свободы.
3. Абсолютное движение - движение тела относительно условно неподвижной системы отсчета.
4. Абсолютное равнодушие в голосе, ни смотря на вопросительный тон - ни малейшей заинтересованности в судьбе пациента. Что-то меня это настораживает.
5. Альтернативная модель: условное единство
6. Анализ условного консультанта
7. Безумная, ужасная и абсолютно восхитительная
8. Будущее и загробная жизнь – абсолютно разные вещи
9. В каких случаях не применяется условно-досрочное освобождение от отбывания от наказания?
10. Вопрос 3. Условно-досрочное освобождение и замена неотбытой части наказания более мягким видом наказания.
11. Входите в РАдость, РАй –Радостное Абсолютное Осознание Единства Целостного присутствия Вселенской Любви и Гармонии.