Определение первообразной и её свойства
Вопрос 1.
Определение первообразной и её свойства
Пусть функция  задана на некотором интервале
задана на некотором интервале 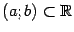 . Если найдётся такая функция
. Если найдётся такая функция  , что при всех
, что при всех  имеет место равенство
имеет место равенство
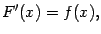
то функция  называется первообразной для функции
называется первообразной для функции  .
.
Пример 1.1 Рассмотрим функцию  на всей числовой оси
на всей числовой оси  -- на интервале
-- на интервале  . Тогда функция
. Тогда функция  -- это первообразная для
-- это первообразная для  на
на 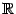 .
.
Для доказательства найдём производную от  :
:
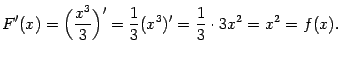
Поскольку равенство верно при всех 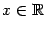 , то
, то  -- первообразная для
-- первообразная для  на
на 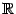 .
.
Аналогичное определение дадим и для случая, когда функция  задана не на одном интервале, а на объединении нескольких непересекающихся интервалов:
задана не на одном интервале, а на объединении нескольких непересекающихся интервалов:
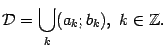
Назовём функцию  первообразной для
первообразной для  , если при всех
, если при всех  выполнено равенство
выполнено равенство  .
.
Правило ингрирования:
Основные правила интегрирования.
1. Вынесение функции из-под знака дифференциала.

Пример:
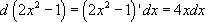
2. Внесение функции под знак дифференциала.
 , где
, где  , т.е. является первообразной
, т.е. является первообразной  .
.
Пример:

[ Найдем первообразную функции 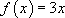
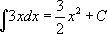 ]
]
 Итог:
Итог: 

Вопрос 2.
Интегрирование путем подведения под знак дифференциала
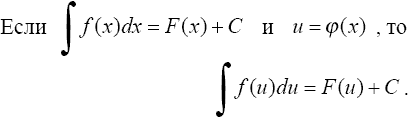
Необходимо иметь в виду простейшие преобразования дифференциала
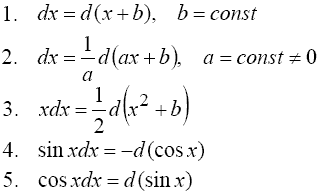
В общем случае:
j'(x)dx=dj(x)
Вопрос 3.
| Интегрирование по частям
|
|
|
Пусть u(x) и v(x) являются дифференцируемыми функциями. Дифференциал произведения функций u и vопределяется формулой
 Проинтегрировав обе части этого выражения, получим
Проинтегрировав обе части этого выражения, получим
 или, переставляя члены,
или, переставляя члены,
 Это и есть формула интегрирования по частям.
Это и есть формула интегрирования по частям.
|
| Пример 1
|
|
|
Вычислить интеграл  .
Решение.
Используем формулу интегрирования по частям .
Решение.
Используем формулу интегрирования по частям 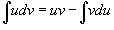 . Пусть . Пусть 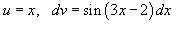 . Тогда . Тогда
 Следовательно,
Следовательно,

|
Интегрирование тригонометрических функций
Рассмотрим интегралы вида
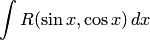 , где
, где  — рациональная функция.
— рациональная функция.
Такие интегралы всегда рационализируются подстановкой 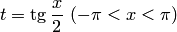 . В самом деле,
. В самом деле,
Выразим далее переменную  через переменную
через переменную 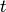 . Так как
. Так как
 , то
, то  , а поэтому
, а поэтому  .
.
Значит
Таким образом, задача свелась к вычислению интеграла от рациональной функции. Поскольку подстановка  — позволяет рационализировать любой интеграл вида
— позволяет рационализировать любой интеграл вида 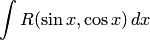 , то её называют универсальной подстановкой. Любой интеграл этого вида выражается через элементарные функции.
, то её называют универсальной подстановкой. Любой интеграл этого вида выражается через элементарные функции.
Вопрос 4.
| Интегрирование рациональных функций
|
|
|
Для интегрирования рациональной функции  , где P(x) и Q(x) - полиномы, используется следующая последовательность шагов: , где P(x) и Q(x) - полиномы, используется следующая последовательность шагов:
- Если дробь неправильная (т.е. степень P(x) больше степени Q(x)), преобразовать ее в правильную, выделив целое выражение;
- Разложить знаменатель Q(x) на произведение одночленов и/или несократимых квадратичных выражений;
- Разложить рациональную дробь на простейшие дроби, используя метод неопределенных коэффициентов;
- Вычислить интегралы от простейших дробей.
|
| Пример 1
|
|
|
Вычислить интеграл 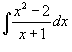 .
Решение.
Сначала выделим правильную рациональную дробь, разделив числитель на знаменатель. .
Решение.
Сначала выделим правильную рациональную дробь, разделив числитель на знаменатель.
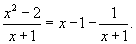 Получаем
Получаем

|
| Интегрирование иррациональных функций
|
|
|
Для интегрирования иррациональной функции, содержащей 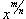 используется подстановка используется подстановка 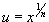 . Чтобы проинтегрировать иррациональную функцию, содержащую несколько рациональных степеней x, применяется подстановка в форме . Чтобы проинтегрировать иррациональную функцию, содержащую несколько рациональных степеней x, применяется подстановка в форме 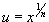 , где n полагается равным наименьшему общему кратному знаменателей всех дробных степеней, входящих в данную функцию. Рациональная функция x под знаком корня n-ой степени, т.е. выражение вида , где n полагается равным наименьшему общему кратному знаменателей всех дробных степеней, входящих в данную функцию. Рациональная функция x под знаком корня n-ой степени, т.е. выражение вида 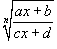 , интегрируется с помощью подстановки , интегрируется с помощью подстановки  . .
|
Найти интеграл  .
.
Решение.
Сделаем подстановку:
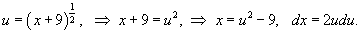
Вычислим интеграл
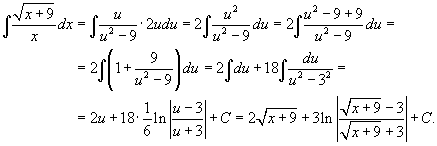
Вопрос 5.
Физический смысл:
1) если задана скорость как функция от времени, то путь за время Т равен интегралу от скорости по времени;
2) если задано ускорение как функция от времени, то изменение скорости равно интегралу от ускорения по времени;
Геометрический смысл: если функция y(x) больше нуля на промежутке [a; b], то площадь криволинейной трапеции, ограниченной графиком функции, осью ОХ и двумя прямыми х=а и х=b, равна интегралу от этой функции по переменной х на данном промежутке.
Вопрос 6.
Формула Ньютона – Лейбница
 Если функция f (x) интегрируема на [a; b], то для любого
Если функция f (x) интегрируема на [a; b], то для любого  существует интеграл
существует интеграл
который называется интегралом с переменным верхним пределом.
Если функция f интегрируема на [a; b], то функция F (x) непрерывна на этом отрезке.
Если функция f интегрируема на [a; b] и непрерывна в  то функция F (x) дифференцируема в
то функция F (x) дифференцируема в  причем
причем
Если функция f непрерывна на [a; b], то на этом отрезке она имеет первообразную F вида
где C – постоянная. Всякая первообразная функции f на отрезке [a; b] удовлетворяет этой формуле.
Одним из основных результатов математического анализа является теорема Ньютона – Лейбница:
 Пусть функция f (x) непрерывна на [a; b], а F (x) – какая-либо первообразная функции f на этом отрезке. Тогда
Пусть функция f (x) непрерывна на [a; b], а F (x) – какая-либо первообразная функции f на этом отрезке. Тогда
Таким образом, для вычисления определенного интеграла нужно найти какую-либо первообразную F функции f, вычислить ее значения в точках a и b и найти разность F (b) – F (a).
Пусть f (x) непрерывна на [a; b], g (t) имеет непрерывную производную на [α; β ],  Тогда если a = g (α ), b = g (β ), то справедлива формула замены переменной в определенном интеграле:
Тогда если a = g (α ), b = g (β ), то справедлива формула замены переменной в определенном интеграле:
Если функции u (x) и v (x) имеют на [a; b] непрерывные производные, то справедлива формула интегрирования по частям:
Вопрос 7.
Вопрос 8.
Определенный интеграл  называется несобственным интегралом, если выполняется, по крайней мере, одно из следующих условий:
называется несобственным интегралом, если выполняется, по крайней мере, одно из следующих условий:
- Предел a или b (или оба предела) являются бесконечными;
- Функция f (x) имеет одну или несколько точек разрыва внутри интервала [a, b].
так, по определению,  . Если этот предел существует и конечен, интеграл
. Если этот предел существует и конечен, интеграл 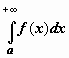 называется сходящимся; если предел не существует или бесконечен, интеграл называется расходящимся.
называется сходящимся; если предел не существует или бесконечен, интеграл называется расходящимся.
Свойства -??
Вопрос 9.
Дифференциа́ льное уравне́ ние — уравнение, связывающее значение производной функции с самой функцией, значениями независимой переменной, числами (параметрами). Порядок входящих в уравнение производных может быть различен (формально он ничем не ограничен). Производные, функции, независимые переменные и параметры могут входить в уравнение в различных комбинациях или все, кроме хотя бы одной производной, отсутствовать вовсе. Дифференциальное уравнение порядка выше первого можно преобразовать в систему уравнений первого порядка, в которой число уравнений равно порядку исходного уравнения.
Вопрос 10.
Уравнением с разделенными переменными называется дифференциальное уравнение вида
f(x)dx + g(y)dy = 0
с непрерывными функциями f(х) и g(y).
Равенство
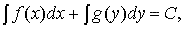
где C — произвольная постоянная, определяет общий интеграл уравнения с разделёнными переменными.
Начальное условие для уравнения f(x)dx + g(y)dy = 0 можно задавать в виде y(x0) = y0 или в виде x(y0) = x0.
Уравнением с разделяющимися переменными называется дифференциальное уравнение вида
f1(x)g1 (y)dx + f2(x) g2(y)dy =0.
Функции f1(x), g1(y), f2(x), g2(y) непрерывны в cвоих областях определения и g1(y)f2(x) ≠ 0.
Разделив обе части уравнения на отличное от нуля произведение g1(y)f2(x), получим уравнение с разделенными переменными
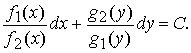
Общий интеграл этого уравнения имеет вид
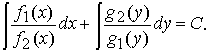
Вопрос 11.
| Линейные дифференциальные уравнения первого порядка
|
|
|
Определение линейного уравнения первого порядка
Дифференциальное уравнение вида
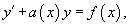 где a(x) и b(x) − непрерывные функции x, называтся линейным неоднородным дифференциальным уравнением первого порядка. Мы рассмотрим два метода решения указанных уравнений:
где a(x) и b(x) − непрерывные функции x, называтся линейным неоднородным дифференциальным уравнением первого порядка. Мы рассмотрим два метода решения указанных уравнений:
- Использование интегрирующего множителя;
- Метод вариации постоянной.
Использование интегрирующего множителя
Если линейное дифференциальное уравнение записано в стандартной форме:
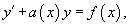 то интегрирующий множитель определяется формулой:
то интегрирующий множитель определяется формулой:
 Умножение левой части уравнения на интегрирующий множитель u(x) преобразует ее в производную произведения y(x)u(x). Общее решение дифференциального уравнения выражается в виде:
Умножение левой части уравнения на интегрирующий множитель u(x) преобразует ее в производную произведения y(x)u(x). Общее решение дифференциального уравнения выражается в виде:
 где C − произвольная постоянная.
где C − произвольная постоянная.
|
Решить уравнение y' − y − xex = 0.
Решение.
Запишем данное уравнение в стандартной форме:
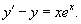
Будем решать это уравнение, используя интегрирующий множитель:
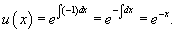
Тогда общее решение линейного дифференциального уравнения определяется выражением:
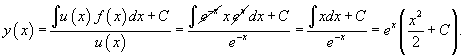
| Уравнение Бернулли
|
|
|
Уравнение Бернулли является одним из наиболее известных нелинейных дифференциальных уравнений первого порядка. Оно записывается в виде
 где a(x) и b(x) − непрерывные функции. Если m = 0, то уравнение Бернулли становится линейным дифференциальным уравнением. В случае когдаm = 1, уравнение преобразуется в уравнение с разделяющимися переменными. В общем случае, когда m ≠ 0, 1, уравнение Бернулли сводится к линейному дифференциальному уравнению с помощью подстановки
где a(x) и b(x) − непрерывные функции. Если m = 0, то уравнение Бернулли становится линейным дифференциальным уравнением. В случае когдаm = 1, уравнение преобразуется в уравнение с разделяющимися переменными. В общем случае, когда m ≠ 0, 1, уравнение Бернулли сводится к линейному дифференциальному уравнению с помощью подстановки
 Новое дифференциальное уравнение для функции z(x) имеет вид
Новое дифференциальное уравнение для функции z(x) имеет вид
 и может быть решено способами, описанными на странице Линейные дифференциальные уравнения первого порядка.
и может быть решено способами, описанными на странице Линейные дифференциальные уравнения первого порядка.
|
| Пример 1
|
|
|
Найти общее решение уравнения y' − y = y2ex.
Решение.
Для заданного уравнения Бернулли m = 2, поэтому сделаем подстановку
 Дифференцируя обе части уравнения (переменная y при этом рассматривается как сложная функция x), можно записать:
Дифференцируя обе части уравнения (переменная y при этом рассматривается как сложная функция x), можно записать:
 Разделим обе части исходного дифференциального уравнения на y2:
Разделим обе части исходного дифференциального уравнения на y2:
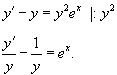 Подставляя z и z', находим:
Подставляя z и z', находим:
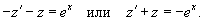 Мы получили линейное уравнение для функции z(x). Решим его с помощью интегрирующего множителя:
Мы получили линейное уравнение для функции z(x). Решим его с помощью интегрирующего множителя:
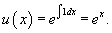 Общее решение линейного уравнения выражается формулой
Общее решение линейного уравнения выражается формулой
 Возвращаясь к функции y(x), получаем ответ в неявной форме:
Возвращаясь к функции y(x), получаем ответ в неявной форме:
 который можно записать также в виде:
который можно записать также в виде:
 Заметим, что при делении уравнения на y2 мы потеряли решение y = 0. В результате, полный ответ записывается в виде:
Заметим, что при делении уравнения на y2 мы потеряли решение y = 0. В результате, полный ответ записывается в виде:

|
Вопрос 13.
Вопрос 12. -??
Вопрос 14.
| Неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами
|
|
|
Структура общего решения
Линейное неоднородное уравнение данного типа имеет вид:
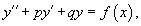 где p, q − постоянные числа (которые могут быть как действительными, так и комплексными). Для каждого такого уравнения можно записать соответствующее однородное уравнение:
где p, q − постоянные числа (которые могут быть как действительными, так и комплексными). Для каждого такого уравнения можно записать соответствующее однородное уравнение:
 Теорема: Общее решение неоднородного уравнения является суммой общего решения y0(x) соответствуюшего однородного уравнения и частного решения y1(x) неоднородного уравнения:
Теорема: Общее решение неоднородного уравнения является суммой общего решения y0(x) соответствуюшего однородного уравнения и частного решения y1(x) неоднородного уравнения:
 Ниже мы рассмотрим два способа решения неоднородных дифференциальных уравнений.
Метод вариации постоянных
Если общее решение y0 ассоциированного однородного уравнения известно, то общее решение неоднородного уравнения можно найти, используя метод вариации постоянных. Пусть общее решение однородного дифференциального уравнения второго порядка имеет вид:
Ниже мы рассмотрим два способа решения неоднородных дифференциальных уравнений.
Метод вариации постоянных
Если общее решение y0 ассоциированного однородного уравнения известно, то общее решение неоднородного уравнения можно найти, используя метод вариации постоянных. Пусть общее решение однородного дифференциального уравнения второго порядка имеет вид:
 Вместо постоянных C1 и C2 будем рассматривать вспомогательные функции C1(x) и C2(x). Будем искать эти функции такими, чтобы решение
Вместо постоянных C1 и C2 будем рассматривать вспомогательные функции C1(x) и C2(x). Будем искать эти функции такими, чтобы решение
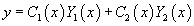 удовлетворяло неоднородному уравнению с правой частью f(x). Неизвестные функции C1(x) и C2(x) определяются из системы двух уравнений:
удовлетворяло неоднородному уравнению с правой частью f(x). Неизвестные функции C1(x) и C2(x) определяются из системы двух уравнений:
 Метод неопределенных коэффициентов
Правая часть f(x) неоднородного дифференциального уравнения часто представляет собой многочлен, экспоненциальную или тригонометрическую функцию, или некоторую комбинацию указанных функций. В этом случае решение удобнее искать с помощью метода неопределенных коэффициентов. Подчеркнем, что данный метод работает лишь для ограниченного класса функций в правой части, таких как
Метод неопределенных коэффициентов
Правая часть f(x) неоднородного дифференциального уравнения часто представляет собой многочлен, экспоненциальную или тригонометрическую функцию, или некоторую комбинацию указанных функций. В этом случае решение удобнее искать с помощью метода неопределенных коэффициентов. Подчеркнем, что данный метод работает лишь для ограниченного класса функций в правой части, таких как
-

-
 где Pn(x) и Qm(x) − многочлены степени n и m, соответственно. где Pn(x) и Qm(x) − многочлены степени n и m, соответственно. В обоих случаях выбор частного решения должен соответствовать структуре правой части неоднородного дифференциального уравнения. В случае 1, если число α в экспоненциальной функции совпадает с корнем характеристического уравнения, то частное решение будет содержать дополнительный множитель xs, где s − кратность корня α в характеристическом уравнении. В случае 2, если число α + β i совпадает с корнем характеристического уравнения, то выражение для частного решения будет содержать дополнительный множитель x. Неизвестные коэффициенты можно определить подстановкой найденного выражения для частного решения в исходное неоднородное дифференциальное уравнение.
Принцип суперпозиции
Если правая часть неоднородного уравнения представляет собой сумму нескольких функций вида
 то частное решение дифференциального уравнения также будет являться суммой частных решений, построенных отдельно для каждого слагаемого в правой части.
то частное решение дифференциального уравнения также будет являться суммой частных решений, построенных отдельно для каждого слагаемого в правой части.
|
Вопрос 15.
http: //www.bez-dvoek.ru/matem/dif3/dz12.htm
Вопрос 16.
http: //mathhelpplanet.com/static.php? p=sistemy-differentsialnyh-uravnenii
Вопрос 17.
http: //www.pm298.ru/diffur7.php
Вопрос 1.
Определение первообразной и её свойства
Пусть функция  задана на некотором интервале
задана на некотором интервале 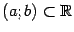 . Если найдётся такая функция
. Если найдётся такая функция  , что при всех
, что при всех  имеет место равенство
имеет место равенство
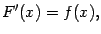
то функция  называется первообразной для функции
называется первообразной для функции  .
.
Пример 1.1 Рассмотрим функцию  на всей числовой оси
на всей числовой оси 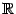 -- на интервале
-- на интервале 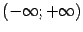 . Тогда функция
. Тогда функция  -- это первообразная для
-- это первообразная для  на
на 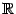 .
.
Для доказательства найдём производную от  :
:
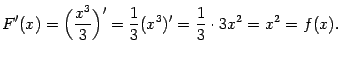
Поскольку равенство верно при всех 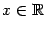 , то
, то  -- первообразная для
-- первообразная для  на
на 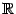 .
.
Аналогичное определение дадим и для случая, когда функция  задана не на одном интервале, а на объединении нескольких непересекающихся интервалов:
задана не на одном интервале, а на объединении нескольких непересекающихся интервалов:
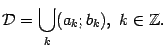
Назовём функцию  первообразной для
первообразной для  , если при всех
, если при всех  выполнено равенство
выполнено равенство  .
.
Правило ингрирования:
Основные правила интегрирования.
1. Вынесение функции из-под знака дифференциала.

Пример:
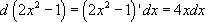
2. Внесение функции под знак дифференциала.
 , где
, где  , т.е. является первообразной
, т.е. является первообразной  .
.
Пример:

[ Найдем первообразную функции 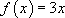
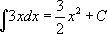 ]
]
 Итог:
Итог: 

Вопрос 2.
Популярное:

