Интерпретация значения величины.

1) Если отношение шансов =1, то шанс для первой группы равен шансу для второй группы

2) Если отношение шансов > 1, то шанс для первой группы больше шанса для второй группы

3) Если отношение шансов < 1, то шанс для первой группы меньше шанса для второй группы

Результаты расчета описательной статистики называются оценками, если они используются по отношению к популяции, из которой отбирались участники исследования. Популяционными характеристиками, парными для оценок, являются параметры. Оценки одного и того же параметра можно получить с помощью различных статистических методов. Оценка должна быть одновременно значимой и точной.
Стратегия отбора объектов из популяции подразумевает, что значимость можно обеспечить методом отбора. Обычно применяется стратегия случайной или вероятностной выборки: если каждый член популяции имеет равные шансы для участия в исследовании, то, в среднем, выбранная группа представительна для населения в целом и, более того, любое отклонение от ожидаемого можно объяснять случайностью. Можно вычислить вероятность отклонения из ожидаемого значения при условии, что соблюдался случайный принцип отбора. Те же самые рассуждения можно использовать для оценки параметров населения в целом, вычисленных на основе исследуемой группы. Например, в качестве оценки среднего значения какой-либо характеристики населения в целом берется арифметическое среднее в исследуемой группе. Любое существующее отличие между средним в исследуемой группе и в целой популяции относят к случайным колебаниям процесса отбора участников исследуемой группы. Если исследуемая группа была отобрана по случайному принципу, то можно вычислить вероятность любой величины этого отличия. Если отличие между оценкой, сделанной при анализе исследуемой группы, и параметром населения в целом нельзя объяснить случайностью, оценка считается смещенной. Схема наблюдений или эксперимента должна обеспечивать значимость оценок, и случайная выборка является одним из фундаментальных принципов статистической стратегии.
В медицине при проведении исследований для сравнения различных групп применяется вторая стратегия статистики. Типичным примером является клиническое исследование с контрольной группой: отбор пациентов с похожими характеристиками осуществляется на основе заранее определенных критериев. На этой стадии не обращают никакого внимания на представительность выборки. Каждый участвующий в исследовании пациент в соответствии с процедурой рандомизации зачисляется либо в исследуемую группу, участники которой получают стандартное лечение и дополнительно новое исследуемое лекарство, либо в контрольную группу, участники которой получают стандартное лечение и плацебо. В этой схеме случайное распределение пациентов по группам заменяет случайный отбор участников. Различие между двумя группами можно оценить статистически, так как, согласно гипотезе об отсутствии эффективности нового лекарства, можно вычислить вероятность любого ненулевого различия.
В эпидемиологии обычно невозможно подобрать группы людей, подвергавшихся и не подвергавшихся вредному воздействию, используя стратегию случайной выборки. Тем не менее, можно применять статистические методы так, как если бы анализируемые группы были отобраны или распределены случайным образом. Правильность такого допущения в большой степени зависит от схемы исследования. Это особенно важно в биологической медицине, где планирование эпидемиологического исследования имеет превалирующее значение над статистическими методами.

" Сигнал" и " шум"
Термин случайная величина относится к такой переменной, для каждого значения которой существует определенная вероятность принятия этого значения. Теоретической схемой распределения значений случайной величины является модель популяции. Исследуемая группа соответствует распределению частоты принятия значений. Это полезный метод графического изображения данных; он заключается в составлении гистограммы распределения со значениями интересующей переменной вдоль горизонтальной оси и частотой ее появления, то есть относительной частотой, вдоль вертикальной оси. Построение графика позволяет сразу увидеть, какие значения принимаются чаще всего, и как выборка распределена вокруг некоторого центрального значения, например, арифметического среднего.
Для случайных величин и их распределений вероятности используются термины параметры, среднее ожидаемое значение (вместо арифметического среднего) и дисперсия. Такие теоретические модели описывают изменчивость явления. В теории информации " сигнал" представлен тенденцией к схождению (например, средней величиной), а " шум" отражает разброс (дисперсию).
Для пояснения статистических заключений мы будем использовать биномиальную модель. В следующих разделах рассматриваются понятия точечной оценки и доверительных интервалов, тестов гипотез, вероятности принятия ошибки, а также статистической мощности исследования.

Пример: биномиальное распределение
В биологической медицине и эпидемиологии наиболее важной моделью случайных переменных является биномиальное распределение. Это связано с тем, что большинство явлений описываются номинальными переменными, имеющими только два состояния, например, наличие или отсутствие болезни, живой или мертвый, выздоровевший или заболевший. В подобных случаях предметом исследования является вероятность осуществления (успеха) представляющего интерес события (например, наличие заболевания, жизнь или выздоровление участника) и факторы или переменные, которые могут повлиять на эту вероятность. Рассмотрим трех рабочих (n = 3) и предположим, что нужно определить вероятность ухудшения зрения (да или нет). Результат исследования соответствует положительным наблюдениям, представленным в таблице 28.10.

Таблица 28.10 Возможные результаты бимодального эксперимента (ДА= 1, НЕТ = 0) и их вероятности (при n = 3)

Рабочий	Вероятность
A	B	C

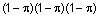
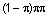
Вероятность любой комбинации событий можно легко вывести из предположения, что индивидуальные вероятности получения положительных результатов для каждого рабочего одинаковы и независимы друг от друга. Поскольку интерес представляет общее число успехов вне зависимости от их последовательности, можно реорганизовать таблицу соответствующим образом (см. таблицу 28.11) и определить общую формулу вероятности x (положительный результат), то есть P(x) как:

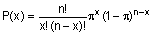
где x - количество положительных результатов, а x! обозначает факториал x, то есть x! = x(x-1)(x-2)…1.

Таблица 28.11 Возможные результаты бимодального эксперимента (ДА= 1, НЕТ = 0) и их вероятности (при n = 3)

Количество успешных результатов	Вероятность

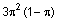
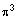
В ситуации " больной или не больной" индивидуальная вероятность успеха относится к состоянию исследуемого объекта; в эпидемиологии эта вероятность называется " распространенностью". Для ее оценки используют долю выборки:
p = x/n
с дисперсией

В гипотетическом бесконечном ряду повторяющихся выборок одного и того же n мы будем получать различные соотношения p = x/n с вероятностями, определяемыми формулой биномиального распределения. " Истинное" значение оценивают для каждой доли выборки, а доверительный интервал, то есть набор вероятных значений для полученных данных и заранее определенного уровня достоверности (например, 95%), определяют из биномиального распределения как набор значений , при котором вероятность x превышает заранее установленное значение (например, 2, 5 %). Для гипотетического эксперимента, в котором наблюдаются 15 положительных результатов (x = 15) в 30 испытаниях (n = 30), оцениваемая вероятность успеха равна:

p = x/n = 15/30 = 0, 5

Доверительный интервал 95% вероятности для, полученный из таблицы 28.12, составляет 0, 334 - 0, 666. Каждая ячейка таблицы показывает вероятность 15 положительных результатов (х = 15) в 30 испытаниях (n = 30), вычисленных по формуле биномиального распределения; например, для = 0, 30 мы имеем

Для больших n и p - близком к 0, 5, можно использовать приближение, основанное на распределении Гаусса

где 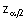- значение стандартного распределения Гаусса для вероятности:

- выбранный уровень доверительности. Для рассматриваемого примера p = 15/30 = 0, 5; n = 30, и из таблицы стандартных распределений можно получить 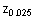= 1, 96. Подставляя p = 0, 5, n = 30, и 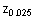= 1, 96 в вышеприведенную формулу распределения Гаусса, получаем доверительный интервал 95% вероятности, равный 0, 321 - 0, 679. Заметим, что полученная величина близка к точному значению, вычисленному ранее.
При изучении изменений какого-либо явления во времени составляется динамический ряд.
Динамическим рядом изучается совокупность однородных статистических величин, показывающего изменение какого-либо явления на протяжении определенного промежутка времени.

Величины, составляющие динамический ряд, называются уровнями ряда.
Уровни динамического ряда могут быть представлены:

— абсолютными величинами;

— относительными величинами (в том числе показателями интенсивными, экстенсивными, соотношения);

— средними величинами.

Динамические ряды бывают двух видов:
— Моментный динамический ряд состоит из величин, характеризующих явление на какой-то определенный момент (дату). Например, каждый уровень может характеризовать численность населения, численность врачей и т.д. на конец какого-то года.
— Интервальный динамический ряд состоит из величин, характеризующих явление за определенный промежуток времени (интервал). Например, каждый уровень такого ряда может характеризовать смертность, рождаемость, заболеваемость, среднегодовую занятость койки за какой-то год.

Примеры

Интервальный динамический ряд, состоящий из интервальных величин.

Динамика рождаемости в Санкт-Петербурге (на 1000 жителей): 1990 - 10, 8 1993 - 6, 6 1991- 9, 3 1994 - 7, 1

1992 - 7, 6

Моментный динамический ряд, состоящий из абсолютных величин. Динамика среднегодовой численности населения Санкт-Петербурга (в тыс.):

1990 - 5035, 0 1993 - 4917, 5

1991 - 5019, 3 1994 - 4860, 7

1992 - 4978, 1

Динамический ряд можно подвергнуть преобразованиям, целью которых является выявление особенностей изучаемого процесса, а также достижение наглядности в характеристике того или иного явления.
Для определения тенденции изучаемого явления рассчитывают показатели динамического ряда:

— абсолютный прирост;

— показатель наглядности;

— показатель роста (снижения);

— темп прироста (снижения).

Абсолютный прирост представляет собой разность между последующим и предыдущим уровнем. Измеряется в тех же единицах, в которых представлены уровни ряда.

Показатель наглядности показывает отношение каждого уровня ряда к одному из них (чаще начального), принятому за 100%.
Показатель роста (убыли) показывает отношение каждого последующего уровня к предыдущему, принятому за 100%.
Темп прироста (убыли) показывает отношение абсолютного прироста (снижения) каждого последующего уровня к предыдущему уровню, принятому за 100%.
Если показатель роста (убыли) показывает сколько процентов от предыдущего уровня составляет последующий уровень, то темп прироста показывает на сколько процентов увеличился (снизился) последующий уровень по сравнению с предыдущим. Поэтому, темп прироста можно рассчитать и по следующей формуле:

темп прироста = показатель роста—100%
Динамический ряд и его показатели могут быть представлены в виде таблицы (табл. 5.4).

Расчет показателей динамического ряда.

1) Абсолютный прирост (снижение):

1991г. 53, 9 - 58, 5 =-4, 6 тыс.

1992 г. 51, 1 - 58, 9 =-2, 8 тыс.

Таблица 5.4
Динамика численности больничных коек в стационарах системы МЗ РФ Санкт-Петербурга
Годы Число больничных коек (тыс.) Абсолютный прирост (убыль) (тыс.) Показатель наглядности, % Показатель роста (убыли), % Темп прироста (убыли), %
1990 58, 5 - 100, 0 - -
1991 53, 9 -4, 6 92, 1 92, 1 -7, 9
1992 51, 1 -2, 8 87, 4 94, 8 -5, 2
1993 49, 3 -1, 8 84, 3 96, 5 -3, 5
1994 47, 8 -1, 5 81.7 96, 9 -3, 1

Рассчитанные показатели динамического ряда свидетельствуют об убыли числа больничных коек в Санкт-Петербурге, однако темп их убыли снижается.

Выравнивание динамического ряда

Иногда динамика изученного явления представлена не в виде непрерывно меняющегося в одном направлении явления, а скачкообразными изменениями.

В таких случаях используют различные методы выравнивания динамического ряда:

— укрупнение интервалов;

— расчет скользящей средней;

— метод наименьших квадратов.

Укрупнение материала можно производить за определенные промежутки времени (за квартал, за один, два, три года и т.д.).

Пример выравнивания динамического ряда с помощью укрупнения интервалов приведены в таблице 5.5.
Таблица 5.5
Годы Средняя длительность пребывания больного на терапевтической койке (в днях) Укрупненный интервал (годы) Средняя длительность пребывания больного на терапевтической койке (в днях)
1987 19, 9
1987-1988 19, 5
1988 19, 0
1989 19, 2
1989-1990 19, 3
1990 19, 3
1991 18, 5
1991-1992 17, 8
1992 17, 0

Произведено укрупнение интервала за два года и рассчитана средняя длительность пребывания больного на койке для каждого интервала. 1987-1988 (19, 9 + 19, 9)/2 = 19, 5

1989-1990 (19, 2 + 19, 3)/2 = 19, 3

1991-1992 (18, 5 + 17, 0)/2 = 17, 8

Показатели преобразованного динамического ряда рассчитываются по общепринятой методике.

Влияние случайных колебаний на уровни динамического ряда можно устранить и с помощью скользящей средней. При ее расчете лучше использовать интервалы, включающие три хронологические периода.

Пример выравнивания динамического ряда методом скользящей средней в таблице 5.6.

Таблица 5.6

Динамика средней длительности пребывания больного на терапевтической койке до— и при переходе стационаров Санкт-Петербурга на новые условия хозяйствования
Годы Средняя длительность пребывания больного на терапевтической койке (в днях) Скользящая средняя Скользящая средняя по Урбаху
1987 19, 9-у, - 19, 7
1988 19, 0 -у2 19, 4 19, 4
1989 19, 2-уд 19, 2 19, 2
1990 19, 3--у4 19, 0 19, 0
1991 18, 5-у5 18, 3 18, 3
1992 17, 0 — у6 - 17, 2

Динамика средней длительности пребывания больного на терапевтической койке до— и при переходе больниц Санкт-Петербурга на новые условия хозяйствования

Для выравнивания динамического ряда произведено вычисление скользящей средней с использованием интервала в три года:

1988г. (19.9+ 19, 0+ 19, 2)/3= 19, 4

1989 г. (19, 0 + 19, 2 + 19.3)/3 = 19, 2

1990 г. (19, 2 + 19.3 + IB, 5)/3 = 19, 0

1991г. (19, 3 + 18, 5 + 17, 0) / 3 = 18, 3

Однако этот метод исключает из анализа средние величины первого и последнего уровня.

Поэтому для более точного определения тенденции изучаемого явления можно рассчитать скользящие средние крайних уровней по формуле Урба-ха:

1987 г. (7у, + 4у2 - 2Уо) /9= (7 • 19, 9 + 4 • 19 - 2 • 19, 2) / 9 = 19, 7

1992 г. (7у6 + 4у5 — 2у4) / 9 = (7 • 17, 0 + 4 • 18, 5 - 2 • 19, 3) / 9 = 17, 2

Метод наименьших квадратов дозволяет наиболее точно выравнивать тенденции изучаемого явления.

Он позволяет рассчитать точки прохождения такой прямой линии, от которой имеющаяся эмпирическая находится на расстоянии наименьших квадратов от других возможных линий.
Динамический ряд в случае применения данного метода должен иметь не менее 5 хронологических дат, количество их должно быть нечетным, а интервалы между ними — одинаковыми.
Пример выравнивания динамического ряда методов наименьших квадратов приведен в таблице 5.7.
Таблица 5.7
Динамика младенческой смертности в Санкт-Петербурге (на 1000 родившихся живыми) за 1988—1992 гг.
Хронологические даты (годы) Младенческая смертность, У Порядковый номер хронологической даты от центральной, X х • у X2 Выравненные уровни младенческой смертности
1988 19, 1 -2 -38, 2 4 19, 0
1989 17, 4 -1 -17, 4 1 18, 3
1990 18, 2 0 0 0 17, 5-0, 0
1991 17, 1 1 17, 1 1 16, 8
1992 15, 5 2 31, 0 4 16, 0
1у = 87, 3 I = -7, 5 ху ' 1х2 = 10

Дата искомой прямой линии округляются по следующей формуле:

У, = а0 + а, -х, где а0 — это хронологическая средняя (значение центральной хронологической даты), которая вычисляется по формуле:

ао = ~Y> гДе

S — сумма хронологических дат (периодов); Еу— сумма всех значений изучаемого явления.

87, 3

а0=^ = 17, 5

а| — это коэффициент поправки искомого расстояния, который определяется по формуле:

I*2

х — порядковый номер (расстояние) хронологических дат от центральной, принятой за 0.

Сумма произведений х-у определяется с учетом алгебраических знаков.

-7, 5

- ТГ " - °'75

Зная величины а0 и a j, подставляем их в уравнение:

у, = а0 + ai -х и, придавая последовательные значения чисел ряда х, получим выравненный динамический ряд младенческой смертности.
1988….у.=17, 5+(-0, 75)-(-2)=19
1969….у2=17, 5+(-0, 75)-(-1)=18, 3
1991у, =17, 5+(-0, 75)-(1)=16, 8

1992 У5= 17, 5 + (-0, 75)-(2) = 16, 0

Содержание.

Введение
Основные понятия медицинской статистики.
Статистические оценки параметров распределения.
Динамические ряды.
Заключение
Список литературы

Введение.

Проблема использования статистики в медицине и биологии связана с более общими проблемами развития науки, которые особенно четко стали проявляться в последние 20—30 лет. Прогресс информационных технологий привел к тому, что общение исследователей стало глобальным, более интенсивным, а информационная насыщенность научных сообщений значительно возросла. Для того чтобы убедиться в этом, достаточно сравнить современную биомедицинскую статью с аналогичной журнальной статьей 20—30-летней давности. Подобный " информационный взрыв" привел к возникновению информационного кризиса, одна из составляющих которого в биомедицине — анализируемая нами проблема некачественного использования статистики в экспериментальных биомедицинских исследованиях.

Заключение.

Медико-статистические показатели периодически пересматриваются в соответствии с новыми задачами здравоохранения, развитием медицинской науки и практики, технической оснащенности служб здравоохранения.

Федеральное агенство по образованию

Ульяновский государственный университет

Институт медицины, экологии и физической культуры

Медицинский факультет

Реферат на тему:

«Статистический анализ результатов исследований»

Выполнил:

Студент группы ЛД-О-11/1

Казаков Евгений

Ульяновск, 2012 г.

Список литературы

http: //www.statsoft.ru/statportal/tabID__50/MId__449/ModeID__0/PageID__305/DesktopDefault.aspx

http: //lib.rus.ec/b/165766/read

http: //download-book.ru/organizatsija-zdravoohranenija/nagljadnaja-statistika-v-meditsine

http: //www.mediasphera.aha.ru/mjmp/99/12/r12-99-1.htm

⇐ Предыдущая 1 2 34