
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Девиации, порождаемые СМС, креновая и электромагнитные девиацииСтр 1 из 26Следующая ⇒
КОНСПЕКТ ЛЕКЦИЙ ПО ДИСЦИПЛИНЕ «ТЕХНИЧЕСКИЕ СРЕДСТВА СУДОВОЖДЕНИЯ Раздел 1. Магнитные компасы Раздел 1.1. Судовое магнитное поле (6 часов). Раздел 1.2. Судовые магнитные компасы (6 часов) Раздел 1.3. Уничтожение составляющих девиации МК (5 часов) Раздел 2. Гидроакустические приборы и индукционные лаги. Гироскопические приборы и устройства. Раздел 2.1. Гидроакустические методы измерений (4 часа) Раздел 2.2. Основы теории и работы гидроакустических приборов (6 часов) Раздел 2.3. Индукционные лаги (2 часа) Раздел 2.4. Перспективная структура ИСОН (1 час). Раздел 2.5. Основы прикладной теории гироскопов и акселерометров (11 часов) Раздел 2.6. Основы прикладной теории гирокомпасов (14 часов) Раздел 2.7. Передача и обмен данными между приборами (2 часа) Раздел 2.8. Гиротахометры (2 часа) Раздел 2.9. Автоматическое управление движением судна(2 часа)
Раздел 1. Магнитные компасы 1.1. Судовое магнитное поле (6 часов). Основные характеристики земного и судового магнитных полей. Уравнения Пуассона и А. Смитта. Судовые магнитные силы (СМС) Общая характеристика земного магнитного поля
 . .
 . .
Наряду с указанным, рассматривают проекции Н и Z вектора Т на плоскость горизонта и на местную вертикаль, соответственно. Эти составляющие определяются следующими равенствами:
Земное магнитное поле претерпевает медленное годовое изменение, а также достаточно быстрые вариации, обусловленные, например, активизацией процессов на Солнце. Кроме того, на равномерность магнитного поля Земли существенное влияние оказывают местные магнитные аномалии. магнитомягкие материалы намагничиваются компонентами магнитного поля Земли. Будем представлять судовое и земное магнитные поля в виде соответствующих составляющих X¢, Y¢, Z¢ и X, Y, Z (рис. 4.1) векторов напряженности (или индукции) этих полей по осям системы координат охуz, жёстко связанной с судном. Особенности намагничивания магнитомягких материалов земным магнитным полем заключается в том, что они будучи намагниченными од
 ставляющие аХ, dХ и gХ, направленные по осям ох, оу и oz, соответственно (Рис. 4.1). Здесь а, d и g – коэффициенты пропорциональности, определяющие величину указанных составляющих в долях намагничивающего поля. Аналогично, материал, намагниченный составляющей Y земного поля, будет создавать собственное поле с компонентами bY, eY и hY, а намагниченный составляющей Z – с компонентами cZ, fZ и kZ. ставляющие аХ, dХ и gХ, направленные по осям ох, оу и oz, соответственно (Рис. 4.1). Здесь а, d и g – коэффициенты пропорциональности, определяющие величину указанных составляющих в долях намагничивающего поля. Аналогично, материал, намагниченный составляющей Y земного поля, будет создавать собственное поле с компонентами bY, eY и hY, а намагниченный составляющей Z – с компонентами cZ, fZ и kZ.
Учитывая сказанное, результирующие напряженности судового магнитного поля вдоль осей, связанных с судном, можно представить в виде следующих равенств (рис. 1.33): X¢ = X + aX + bY + cZ + P, Y¢ = Y + dX + eY +fZ + Q, (4.1) Z¢ = Z + gX + hY + kZ + R, где H, Q и R – компоненты магнитного поля, порождаемые постоянным судовым магнетизмом. Уравнения (4.1) получили название уравнений Пуассона, а коэффициенты а…к – коэффициентов Пуассона. Полученные уравнения характеризуют структуру судового магнитного поля и являются исходными для проведения различных оценок на практике. Однако для процесса судовождения основной интерес представляет связь параметров судового поля с ошибками МК, т.е. с той девиацией, которая возникает у компаса, установленного в заданном месте на судне. Эта девиация определяется отклонением от плоскости магнитного меридиана горизонтальнойсоставляющей Н¢ (рис. 4.1) судового магнитного поля, образуемой геометрической суммой векторов X¢ и Y¢ , в направлении которой устанавливаются оси магнитов картушки компаса. Найдём соотношения, определяющие указанную связь. Уравнение девиации
может быть определена следующим равенством:
В свою очередь, из рисунка следует, что H¢ sin Подставляя в полученные равенства значения X¢ и Y¢ из уравнений Пуассона (4.1), найдём: H¢ sin H¢ cos (4.5) В последних равенствах учтём, что Х=Н cosMK, Y= - H sinMK. (4.6) Тогда получим:
Раскрывая квадратные скобки равенств (4.7), найдём:
Обозначим
Введём следующие обозначения:
и подставим их в равенства (4.10). В результате будем иметь:
(4.12) Поделив первое равенство (4.12) на второе, получим искомое выражение для тангенса девиации магнитного компаса:
(4.13) Это выражение получило название формулы Арчибальда Смита по имени английского учёного Х1Х века. Оно определяет зависимость девиации МК от параметров А¢ …E¢ и магнитных курсов судна. Параметры A¢ …E¢ получили название коэффициентов девиации. На практике чаще представляют девиацию МК в функции компасных курсов судна [5]. Для того чтобы получить указанное выражение умножим равенство (4.13) на его знаменатель. В результате будем иметь:
Раскрывая скобки и перенося все члены кроме первого в правую часть равенства, найдём:
Учитывая, что КК=МК -
Судовые магнитные силы
Результирующий вектор горизонтальной составляющей напряженности судового магнитного поля в районе картушки магнитного компаса удобно представлять его отдельными компонентами, которые получили название судовых магнитных сил (СМС). Состав этих сил и их взаимную ориентацию можно определить, используя равенства (4.12), в которых левые и правые их части следует умножить на
 , входящие в полученное уравнение. Анализируя указанные коэффициенты, обратим внимание на то обстоятельство (см. равенства (4.9)), что СМС , входящие в полученное уравнение. Анализируя указанные коэффициенты, обратим внимание на то обстоятельство (см. равенства (4.9)), что СМС   зависят от параметров и расположения на судне магнитомягких материалов, а СМС зависят от параметров и расположения на судне магнитомягких материалов, а СМС 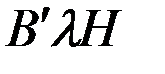 и и  - как магнитомягких, так и магнитотвёрдых. Также нетрудно заметить, что первая группа СМС зависит от величины горизонтальной составляющей Н напряженности магнитного поля Земли, в то время как вторая группа – от вертикальной составляющей Z. Все СМС не зависят от курса судна. Поскольку СМС представляют собой компоненты вектора напряжённости судового магнитного поля, они также являются векторными величинами. - как магнитомягких, так и магнитотвёрдых. Также нетрудно заметить, что первая группа СМС зависит от величины горизонтальной составляющей Н напряженности магнитного поля Земли, в то время как вторая группа – от вертикальной составляющей Z. Все СМС не зависят от курса судна. Поскольку СМС представляют собой компоненты вектора напряжённости судового магнитного поля, они также являются векторными величинами.
Для определения ориентации СМС обратимся к равенствам (4.17). Будем условно полагать, что все СМС, кроме В этом случае указанные равенства примут вид:
Для того чтобы определить направление СМС
Этим равенствам соответствует схема векторов, показанная на рис. 4.4. Из рисунка следует, что СМС Поступая аналогично, определим направление СМС С¢ lН. Для этого будем полагать неравными нулю только силы lН и С¢ lН. Тогда получим:
Схема векторов, соответствующая равенствам (4.20), имеет вид, показанный на рис. 4.5. Из рисунка следует, что СМС С¢ lН направлена под углом 900+МК по отношению к магнитному меридиану и, следовательно, перпендикулярно СМС В¢ lН.
Таким образом, в общем случае ориентация векторов судовых магнитных сил будет иметь вид, показанный на рис. 4.6. На этом рисунке Nk соответствует направлению компасного меридиана, в плоскости которого находится результирующий вектор Н¢ напряжённости судового магнитного поля. Проектируя векторы СМС на направление компасного меридиана, найдём выражение, определяющее значение вектора Н¢:
Индукционные МК Принцип действия эхолота Основной задачей навигационного эхолота является определение расстояния от излучающей поверхности его антенны до дна. Решение этой задачи осуществляется путем измерения времени прохождения гидроакустической посылкой, формируемой эхолотом, до дна и обратно. Посылка, как правило, представляет собой короткий импульс, промодулированный сигналом несущей частоты. Импульсное излучение характеризуется формой импульса, его длительностью Ти (рис. 1.1), частотой или периодом Т следования импульсов. Чаще всего используются импульсы прямоугольной формы (рис.1.1.а), которые являются наиболее энергонасыщенными. В недавнем прошлом достаточно широко применялась экспоненциальная форма (рис. 1.1, б) в силу того, что ее было проще реализовать технически.
Импульс, выработанный антенной А1, достигнет дна в точке О и отразившись вернется обратно, спустя некоторое время
Исходя из сказанного, типовой состав эхолота должен включать в себя: § антенные устройства; § устройство, формирующее сигнал посылки (передающее устройство) ПРД; § приемное устройство ПРМ, осуществляющее усиление выходного сигнала антенны А2 и преобразование его к виду, удобному для дальнейшего использования; § командное устройство КУ, управляющее работой эхолота; § устройства И отображения и регистрации информации. В том случае, если эхолот имеет одну приемно-передающую антенну, он должен включать в себя устройство для переключения антенны с приема на передачу. Рассмотрим особенности устройства и работы каждого из перечисленных блоков.
Передающее устройство Как уже указывалось ранее, для измерения глубины под килем судна, как правило, используется импульсный зондирующий сигнал. Это обусловлено, прежде всего, тем, что импульсное излучение, позволяет достаточно просто избавиться от помехи, обусловленной сигналом объемной реверберации. Этот помеха возникает в результате отражения сигнала посылки от всяких неоднородностей, встречающихся на его пути. Этими неоднородностями могут быть пузырьки воздуха, распределенные в воде, косяки рыб, мусор, зоны высоких температурных градиентов и тому подобное. Рассматриваемый сигнал возвращается к антенне раньше сигнала, отраженного от дна, и практически затухает к моменту приема основного (полезного) сигнала. По понятным причинам в случае непрерывного излучения сигнал объемной реверберации существовал бы постоянно. Наряду с указанным, использование импульсного излучения позволяет применять как для излучения, так и для приема сигналов одну антенну, получить несколько более простые структуры преобразования принятого зондирующего излучения, что, в свою очередь, позволяет упростить и удешевить само изделие. Учитывая это, рассмотрим лишь те вопросы, которые связаны с формированием импульсного сигнала посылки. Параметры посылки должны удовлетворять определенным требованиям, так как от них в значительной мере зависит качество работы эхолота. Прежде всего, должна быть задана несущая частота посылки. От нее в значительной степени зависят затухание сигнала, параметры, характеризующие его отражение от границ раздела сред и различных объектов, а также траектория движения фронта волны. Снижение несущей частоты, как правило, требует увеличения размеров антенных устройств, но способствует увеличению дальности зондирования. Как правило, несущие частоты лежат в ультразвуковом диапазоне, причем их верхние значения обычно не превышают 300 кГц. Длительность импульса Ти (рис. 1.1) также имеет большое значение, так как она совместно с его амплитудой определяет энергию, заключенную в нем, и, следовательно, влияет на предельную глубину, которая может быть измерена. Кроме того, от длительности импульса зависит разрешающая способность эхолота, т.е. та минимальная разность глубин, которая может быть измерена системой. Действительно, в связи с тем, что импульс является носителем единичной информации о текущей глубине, все ее изменения в рамках пространственной протяженности импульса системой зарегистрированы не будут. Учитывая, что импульс проходит удвоенное расстояние - до отражателя и обратно, разрешающая способность системы
На практике длительность импульсов чаще всего лежит в диапазоне от 10-5 с до 10-3 с, что соответствует разности глубин от 10 см до 1, 5 м. Частота следования импульсов обычно выбирается из тех соображений, чтобы в любом рабочем диапазоне последующий импульс излучался только после того, как будет принят отраженный. Иными словами, период Т (рис. 1.1) следования импульсов должен удовлетворять неравенству:
В качестве задающих генераторов в эхолотах, как правило, используют обычные высокочастотные автогенераторы синусоидальных колебаний с трансформаторной, автотрансформаторной или емкостной обратной связью. Модуляторы могут применяться как амплитудные, воздействующие непосредственно на колебания, вырабатываемые генератором сигнала, так и ключевые, обеспечивающие прохождение напряжения задающего генератора только в те промежутки времени, когда они открыты импульсом, поступившим с ГИ. Усиление сигналов по напряжению и мощности осуществляется по классическим схемам. Конкретные схемы усилителей определяются той элементной базой, на которой они построены. В современных эхолотах с целью оптимизации параметров излучения предусматривается возможность изменения в определенных пределах несущей частоты, мощности излучаемого сигнала, а также длительности импульсов и частоты их следования.
Информации Как было указано в первой главе, экономический критерий, определяющий целесообразность производства того или иного вида гироскопической техники, обусловил интерес к новым образцам инерциальных датчиков информации – микромеханическим гироскопам (ММГ) и акселерометрам (ММА). Разработка ММГ началась с середины 80 годов [34] и в настоящее время многие фирмы в России и за рубежом уже освоили их производство. В качестве примеров таких изделий можно назвать [34, 45]: кремниевые ММГ и ММА фирмы " Rockwell International", разработанные в лаборатории им. Ч. Дрейпера (США); кварцевые ММГ и ММА фирмы " Systran Donner" (США); пьезокерамические ММГ фирмы " Murata" (Япония). Среди отечественных фирм, занимающихся разработкой подобных датчиков, следует выделить: ЦНИИ машиностроения, НИИ прикладной механики им. академика В.И.Кузнецова, НПК " Вектор" (все - г. Москва); НИИ командных приборов, Центр микротехники и диагностики России, ГУАП, АОЗТ “Гирооптика” (все г. С. – Петербург) НПП “Темп-Авиа” (г. Арзамас). Принципиальной особенностью этих датчиков является использование при их производстве материалов и технологий современной твердотельной микроэлектроники. Микромеханические инерциальные датчики имеют встроенную электронику управления и обработки информации, малую массу и габариты (доли миллиграммов и единицы миллиметров [8]), малое энергопотребление (доли милливатт), высокую устойчивость к внешним воздействиям. Используемая технология обеспечивает массовое производство и, как следствие этого, уникально низкую стоимость (единицы и десятки долларов) микромеханических датчиков.
На рис. 3.19 в двух проекциях представлена конструктивная схема ММГ камертонного типа. В плане размеры этого датчика составляют, примерно, 2х4 мм, а его толщина – 20 мкм [7].
При наличии вращения основания с угловой скоростью Ω вокруг оси oz, возникают силы F1 и F2 кориолиса, вынуждающие перемещаться инерционные массы. Это приводит к повороту ЧЭ вокруг оси oz на угол φ и смещению масс относительно его плоскости на величину у. В связи с тем, что смещение х инерционных масс носит периодический характер, закон изменения угла φ и смещения у также будет периодическим. Частота указанных колебаний будет определяться частотой питания электростатических двигателей, а их амплитуда, как и у камертонного гироскопа, рассмотренного в параграфе 2.4, будет зависеть от угловой скорости Ω . При исследовании работы прибора в первом приближении можно считать, что параметры колебаний чувствительного элемента в основном определяются моментами сил кориолиса, что позволяет записать уравнение, этих колебаний в следующем виде [8]:
Морской гирокомпас Проблема создания ГК практически неподверженного влиянию качки судна потребовала использования в качестве его чувствительного элемента гироскопа с тремя степенями свободы. Очевидно, что только такой гироскоп, имеющий совершенную систему подвеса ротора, может изолировать последний от влияния углового движения основания, на котором он установлен. Однако, указанный прибор, лишенный всяких корректирующих воздействий, не способен автоматически совмещать свою главную ось с плоскостью меридиана и, тем самым, не может быть гирокомпасом. Очевидно, необходимо создать такую систему коррекции гироскопа, которая бы заставляла его главную ось устанавливаться в меридиан но, по возможности, не порождала бы зависимости ее движения от параметров качки судна. Простейшим образом эта задача решается путем смещения центра массы чувствительного элемента прибора вдоль наружной оси его подвеса. Рассмотрим закон движения главной оси гироскопа при наличии указанного смещения [10]. Будем считать, что гироскоп с тремя степенями свободы, к гирокамере ВК (рис. 1.3) которого с целью смещения его центра масс прикреплен груз Q , установлен на земной поверхности в каком-либо пункте а. Будем также полагать, что в начальный момент времени его главная ось ОА совпадает с плоскостью горизонта и направлена с запада на восток. В этих условиях сила G веса гироскопа, несмотря на наличие расстояния l между его центром тяжести и точкой подвеса О, не будет создавать относительно последней Начальная ориентация гироскопа относительно земной поверхности не будет оставаться неизменной. С течением времени вследствие суточного вращения Земли место установки гироскопа будет перемещаться в пространстве. Если за вращением Земли наблюдать извне со стороны северного полюса, будет видно, что это перемещение совершается против часовой стрелки. Таким образом, по прошествии некоторого времени место установки гироскопа, совершив вместе с Землей поворот вокруг ее оси, переместится в пространстве на некоторый угол и займет новое положение, обозначенное на схеме точкой б. В процессе описываемого перемещения гироскоп, стремящийся сохранить направление своей главной оси неизменным в пространстве, начнет приобретать все увеличивающийся наклон к горизонту. При этом восточный конец главной оси ОА будет непрерывно подниматься над горизонтом, а западный — опускаться. Вместе с гироскопом вокруг оси 0В будет поворачиваться и груз Q. При наличии угла β между главной осью и плоскостью горизонта вектор G уже не будет проходить через точку О подвеса гироскопа, обусловливая тем самым возникновение момента MВ, действующего на гироскоп относительно его внутренней оси подвеса ОВ. Нетрудно заметить, что величина момента MВ определяется произведением Как только момент МВ начнет действовать на гироскоп, возникнет прецессионное движение вокруг наружной оси ОС. В результате главная ось ОА гироскопа, поворачиваясь вокруг оси ОС с угловой скоростью Поскольку, стремясь к меридиану, гироскоп одновременно движется по двум углам α и β , представляет интерес выяснить траекторию движения его главной оси. Для этого обратимся к уравнениям (2.20 [16]), описывающим поведение гироскопа с тремя степенями свободы, основание которого вращается в пространстве с угловыми скоростями ω хо, ω уо и ω zo. Если учесть, что в рассматриваемом случае
Так как в качестве базовой системы координат нами была выбрана горизонтальная система с географической ориентацией осей (рис. 2.20 [16]), указанные угловые скорости будут определяться равенствами (2.38 [16]), в которых относительные скорости
Подставляя равенства (1.3) в уравнения (1.2) и принимая во внимание, что на практике
Популярное:
|
Последнее изменение этой страницы: 2017-03-08; Просмотров: 949; Нарушение авторского права страницы