Проверка гипотезы о равномерном распределении

⇐ ПредыдущаяСтр 4 из 4

Загрузим пакет stats и подпакеты transform, describe.

> restart: with(stats): with(transform): with(describe):

Вводим реализацию выборки (см. данные своего варианта):

> Y: =[10.63, 26.04, 6.09, 23.42, 5.25, 24.87, 3.24, 6.24, 4.96, 13.74,

13.25, 21.71, 20.96, 34.72, 8.71, 9.06, 19.12, 20.02, 8.58, 34.52,

14.29, 32.13, 13.40, 26.62, 20.13, 6.48, 30.30, 9.16, 12.39, 21.48,

5.28, 13.82, 21.77, 32.26, 21.70, 7.87, 29.74, 21.11, 17.79, 17.67,

27.76, 27.34, 5.87, 5.02, 12.32, 25.43, 31.07, 24.85, 15.14, 25.85,

7.14, 12.78, 24.99, 27.51, 22.59, 29.00, 34.62, 17.65, 9.02, 21.51,

11.24, 22.13, 10.48, 13.20, 12.34, 25.25, 31.73, 28.72, 14.11, 9.62,

17.54, 12.87, 27.15, 18.08, 19.94, 29.86, 30.53, 10.30, 33.13, 23.41];

Определим объём выборки (подсчитаем количество значений в выборке) и рассчитаем количество интервалов разбиения k:

> n: =count(Y); k: =round(1+1.4*ln(n));

Проведём сортировку выборки (варианты расположим в порядке возрастания):

> Y1: =statsort(Y);

Находим минимальное и максимальное значения выборки и дли-ну интервала разбиения:

> ymin: =Y1[1]; ymax: =Y1[n]; h: =(ymax-ymin)/k;

Вычислим границы интервалов разбиения:

> Y2: =[seq(ymin+(i-1)*(h+0.0001)..ymin+i*(h+0.0001), i=1..k)];

Находим вектор точек разбиения:

> Z: =[seq(ymin+(i-1)*(h+0.0001), i=1..k+1)];

Составляем интервальный ряд частот Y3 (каждому интервалу поставим в соответствие частоту n_i, т.е. число элементов выборки, попадающих в данный интервал) и вектор частот Y3f:

> Y3: =statsort(transform[tallyinto](Y1, Y2));

> Y3f: =transform[frequency](Y3);

Получим интервальный ряд относительных частот (каждому интервалу поставим в соответствие относительную частоту, т.е. частоту, делённую на объём выборки):

> Y4: =transform[scaleweight[1/n]](Y3);

Строим гистограмму относительных частот:

> Hist: =statplots[histogram](Y4, color=green):

> plots[display](Hist);

По виду гистограммы выдвигаем гипотезу о равномерном распределении генеральной совокупности.

Находим накопленные частоты Y5 (накопленная частота показывает, сколько наблюдалось значений, меньших заданного x) и относительные накопленные частоты Y6:

> Y5: =transform[cumulativefrequency](Y3);

> Y6: =transform[cumulativefrequency](Y4);

Строим график эмпирической функции распределения:

> p: =[seq(plot(Y6[i], Y2[i], color=blue), i=1..k)]: plots[display](p);

Находим точечные оценки математического ожидания m (выборочное среднее значение), дисперсии S и среднего квадратического отклонения s:

> m: =mean(Y);

> S: =variance(Y);

> s: =standarddeviation(Y1);

Находим исправленные оценки дисперсии (несмещённая оценка дисперсии) и среднего квадратического отклонения:

> S1: =S*n/(n-1);

> s1: =sqrt(S1);

Находим точечные оценки параметров равномерного распределения: , где

> a: = m-sqrt(3.0)*s1; b: = m+sqrt(3.0)*s1;

Вычислим вероятности попадания значения случайной величины в первый и последний ( k- ый) интервалы:

> p[1]: =(Z[2]-a)/(b-a);

> p[k]: =(b-Z[k])/(b-a);

Вычислим вероятности попадания значения случайной величины во 2, 3, …, k -1 интервалы по формулам :

> for j from 2 to 6 do p[j]: =(Z[j+1]-Z[j])/(b-a) od;

Находим теоретические частоты np_i:

> for j from 1 to k do n*p[j] od;

Так как все np_i > 5, то пересчёт не делаем, число интервалов остаётся прежним: k = 7.

Сравним эмпирические n_i и теоретические np_i частоты, для этого находим наблюдаемое значение по формуле .

> chi2: =sum((Y3f[i]-n*p[i])^2/(n*p[i]), i=1..7);

По таблице критических точек распределения , по заданномууровню значимости aи числу степеней свободы ν = s-l-1 (s – число интервалов после пересчёта, l – число параметров в гипотетической функции распределения) находят критическую точку . В нашем случае a = 0, 01(см. задание), s = k = 7, l = 2, т.е. ν = 7-2-1=4, тогда .

Так как , то гипотеза о равномерном распределении генеральной совокупности принимается.

Запишем гипотетическую функцию плотности распределения

и построим на одном рисунке гистограмму относительных частот и график плотности гипотетического распределения.

> f: =piecewise(x< a, 0, x> =a and x< =b, 1/(b-a), x> b, 0);

> f1: =plot(f, x=ymin-1..ymax+1):

> plots[display](Hist, f1);

Запишем гипотетическую функцию распределения

и построим её график.

> F: =piecewise(x< a, 0, x> =a and x< =b, (x-a)/(b-a), x> b, 1);

> F1: =plot(F, x=0..ymax+10):

> plots[display](F1);

Проверка гипотезы о показательном распределении

Загрузим пакет stats и подпакеты transform, describe.

> restart: with(stats): with(transform): with(describe):

Вводим реализацию выборки (см. данные своего варианта):

> Y: =[0.63, 16.04, 6.09, 3.42, 9.25, 2.87, 1.34, 11.24, 4.96, 3.74,

9.25, 1.71, 20.96, 6.72, 8.71, 1.06, 19.12, 0.02, 8.58, 31.52,

0.29, 8.13, 17.40, 1.62, 3.13, 18.48, 30.30, 9.16, 2.39, 1.48,

5.28, 13.82, 1.77, 2.26, 1.70, 7.87, 9.74, 21.21, 7.79,.67,

18.76, 8.34, 1.87, 7.02, 2.32, 2.43, 3.07, 4.85, 5.14, 5.85,

1.14, 2.78, 4.99, 7.51, 2.59, 2.00, 11.62, 1.65, 9.02, 1.51,

11.21, 22.13, 0.48, 13.20, 12.34, 5.25, 5.73, 0.72, 14.11, 9.62,

13.54, 12.87, 27.11, 1.08, 5.94, 1.86, 30.53, 6.30, 20.13, 3.41];

> n: =count(Y); k: =round(1+1.4*ln(n));

Проведём сортировку выборки (варианты расположим в порядке возрастания):

> Y1: =statsort(Y);

Находим минимальное и максимальное значения выборки и длину интервала разбиения:

> ymin: =Y1[1]; ymax: =Y1[n]; h: =(ymax-ymin)/k;

Вычислим границы интервалов разбиения:

> Y2: =[seq(ymin+(i-1)*(h+0.0001)..ymin+i*(h+0.0001), i=1..k)];

Находим вектор точек разбиения:

> Z: =[seq(ymin+(i-1)*(h+0.0001), i=1..k+1)];

> Y3: =statsort(transform[tallyinto](Y1, Y2));

> Y3f: =transform[frequency](Y3);

> Y4: =transform[scaleweight[1/n]](Y3);

Строим гистограмму относительных частот:

> Hist: =statplots[histogram](Y4, color=green):

> plots[display](Hist);

По виду гистограммы выдвигаем гипотезу о показательном распределении генеральной совокупности.

> Y5: =transform[cumulativefrequency](Y3);

> Y6: =transform[cumulativefrequency](Y4);

Строим график эмпирической функции распределения:

> p: =[seq(plot(Y6[i], Y2[i], color=blue), i=1..k)]: plots[display](p);

Находим точечные оценки математического ожидания a (выборочное среднее значение), дисперсии S и среднего квадратического отклонения s:

> a: =mean(Y);

> S: =variance(Y);

> s: =standarddeviation(Y1);

> S1: =S*n/(n-1);

> s1: =sqrt(S1);

Находим точечную оценку параметра показательного распределения:

> lambda: =1/a;

Вычислим вероятности попадания значения случайной величины в первый и последний ( k- ый) интервалы:

> p[1]: =int(lambda*exp(-lambda*t), t=0..Z[2]);

p[k]: =int(lambda*exp(-lambda*t), t=Z[k]..infinity);

Вычислим вероятности попадания значения случайной величины во 2, 3, …, k -1 интервалы по формулам :

> for j from 2 to k-1 do p[j]: =int(lambda*exp(-lambda*t), t=Z[j]..Z[j+1]) od;

Находим теоретические частоты np_i:

> for j from 1 to k do n*p[j] od;

Так как на трёх последних интервалах np_i < 5, то объединим эти интервалы и пересчитаем соответствующие вероятности и частоты, при этом число интервалов будет 5:

> p[5]: = p[5]+p[6]+p[7]; Y3f[5]: =Y3f[5]+Y3f[6]+Y3f[7];

Сравним эмпирические n_i и теоретические np_i частоты, для этого находим наблюдаемое значение по формуле , где i = = 1, 2, …, 5, так как три последних интервала объединили.

> chi2: =sum((Y3f[i]-n*p[i])^2/(n*p[i]), i=1..5);

Так как , то гипотеза о показательном распределении генеральной совокупности принимается.

Запишем гипотетическую функцию плотности распределения и построим на одном рисунке гистограмму относительных частот и график плотности гипотетического распределения.

> f: =piecewise(x< 0, 0, x> =0, evalf(lambda*exp(-lambda*x)));

> f1: =plot(f, x=-10..ymax+10):

> plots[display](Hist, f1);

Запишем гипотетическую функцию распределения

и построим её график.

> F: =piecewise(x< 0, 0, x> =0, 1-exp(-lambda*x));

> F1: =plot(F, x=-10..ymax+10):

> plots[display](F1);

Контрольные вопросы к лабораторным работам 4 и 5

1. Что называется генеральной совокупностью, выборкой, реализацией выборки? Привести примеры.

2. Как построить сгруппированный и интервальный статистические ряды?

3. В чём заключается выборочный метод построения математической модели эксперимента?

4. Что называется эмпирической функцией распределения? Какими свойствами она обладает?

5. В чём состоит отличие эмпирической функции распределения от теоретической?

6. Как построить гистограмму частот, относительных частот?

Что называется статистикой, оценкой неизвестного параметра?

7. Какая оценка называется состоятельной, несмещённой, эффективной?

8. Какие оценки математического ожидания и дисперсии генеральной совокупности вы знаете?

9. Что такое интервальная оценка и чем она отличается от точечной?

10.Что такое статистическая, нулевая и альтернативная гипотезы? Какую гипотезу называют простой, сложной, параметрической, непараметрической?

11. Дайте определение статистического критерия. Что такое ошибки первого и второго рода?

12. Какую гипотезу вы проверяете в этой работе? На какой статистике строится соответствующий критерий? Как найти число степеней свободы?

13. Какой смысл имеет уровень значимости критерия?

14. Опишите подробно критерий Пирсона.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Бородин, А.Н. Элементарный курс теории вероятностей и математической статистики / А.Н. Бородин. – Серия «Учебники для вузов. Специальная литература». – СПб.: Лань, 1999. – 224 с.

2. Гмурман, В.Е. Руководство к решению задач по теории вероятностей и математической статистике: учеб. пособие для студентов вузов / В.Е. Гмурман. –11-е изд., перераб. и доп. – М.: Юрайт, 2011. – 405 с.

3. Доугерти, К. Введение в эконометрику: учебник / К. Доугерти; пер. с англ. – М.: ИНФРА-М, 2009. – 465 с.

4. Дьяконов, В.П. Maple 9.5/10 в математике, физике и образовании / В.П. Дьяконов. – М.: СОЛОН-Пресс, 2006. – 720 с.

5. Кремер, Н.Ш. Теория вероятностей и математическая статистика: учебник для вузов / Н.Ш. Кремер. – 2-е изд., перераб. и доп. – М.: ЮНИТИ-ДАНА, 2004. – 573 с.

6. Михайлов, А.Б. Математика. Лаборатор. практикум для самостоят. работы студентов очной, заочной и дистанционной форм обучения всех напр. и спец.: в 2 ч. / А.Б. Михайлов, И.Д. Михайлова, О.В. Саакян, К.А. Михайлов. – Шахты: ФГБОУ ВПО «ЮРГУЭС», 2011. – Ч. 1. – 53 с.

7. Васильев, А.Н. Maple 8: самоучитель / А.Н. Васильев. – М.; СПб; Киев: Диалектика, 2003. – 352 с.

8. Син, Л.И. Методические указания к самостоятельной работе по курсу «Прикладные математические пакеты: Maple»: в 2 ч. / Л.И. Син. – Шахты: ЮРГУЭС, 2003. – Ч. 1 – 19 с.

9.Кельберт, М.Я. Вероятность и статистика в примерах и задачах. Том 1. Основные понятия теории вероятностей и математической статистики / М.Я. Кельберт, Ю.М. Сухов. – М.: МЦНМО, 2010. – 486 с. – URL: http: //www.biblioclub.ru/69109_Veroyatnost_i_ statistika_v_primerakh_i_ zadachakh_Tom_1_Osnovnye_ponyatiya_teorii_veroyatnostei_i_matematicheskoi_statistiki.html

10. Балдин, К.В. Основы теории вероятностей и математической статистики: учебник / К.В. Балдин, В.Н. Башлыков, А.В. Рокосуев; под ред. Балдина К.В. − М.: Флинта, 2010. – 245 с. – URL: http: //www.biblioclub.ru/79333_Osnovy_teorii_veroyatnostei_i_matematicheskoi_statistiki_Uchebnik.html

11. Большакова, Л.В. Теория вероятностей для экономистов / Л.В. Большакова. – М.: Финансы и статистика, 2009. – 105 с. – URL: http: //www.biblioclub.ru/59589_Teoriya_veroyatnostei_dlya_ekonomistov.html

12. Плис, А.И. Mathcad. Математический практикум для инженеров и экономистов / А.И. Плис, Н.А. Сливина. – М.: Финансы и статистика, 2003. – 657 с. – URL: http: //www.biblioclub.ru/ 68904_Mathcad_ Matematicheskii_praktikum_dlya_inzhenerov_i_ekonomistov.html

Приложение 1

(справочное)

Таблица значений функции

Приложение 2

(справочное)

Таблица значений функции Лапласа

Примечание. Для отрицательных

значения функции Лапласа вычисляют, используя свойство

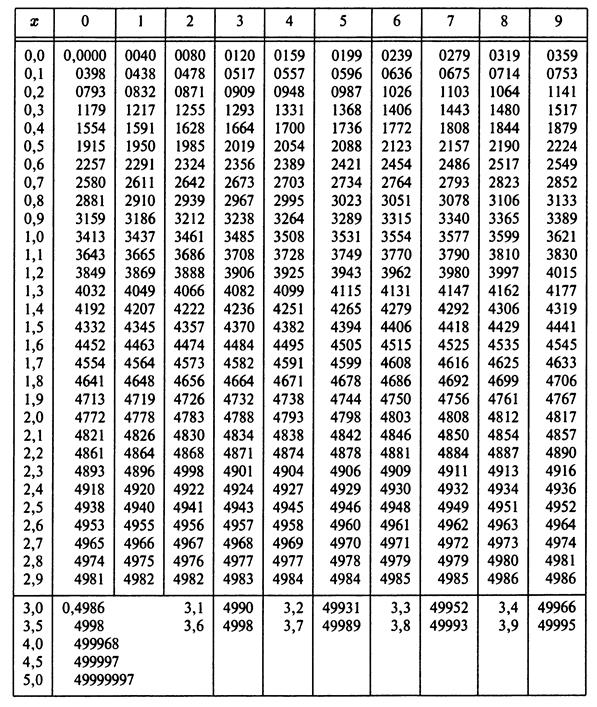
Приложение 3

(справочное)

Таблица значений функции

Продолжение табл.

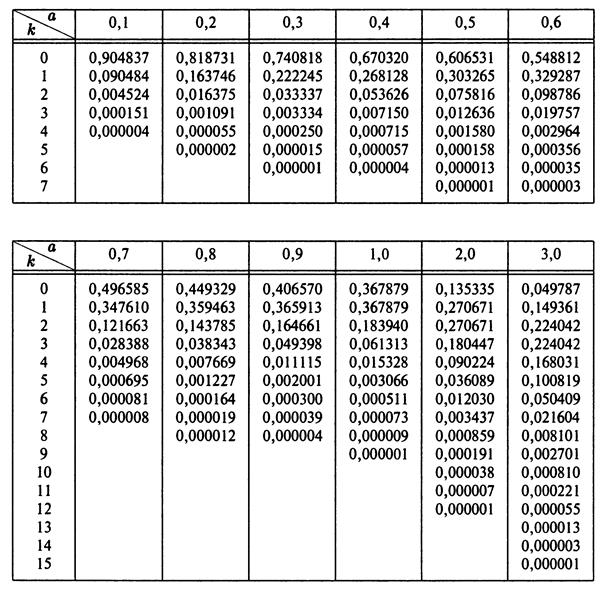
Окончание табл.

Приложение 4

(справочное)

Критические точки распределения χ ²

Число степеней свободы k	Уровень значимости α
0, 01	0, 025	0, 05	0, 95	0, 975	0, 99
	6, 6	5, 0	3, 8	0, 0039	0, 00098	0, 00016
	9, 2	7, 4	6, 0	0, 103	0, 051	0, 020
	11, 3	9, 4	7, 8	0, 352	0, 216	0, 115
	13, 3	11, 1	9, 5	0, 711	0, 484	0, 297
	15, 1	12, 8	11, 1	1, 15	0, 831	0, 554
	16, 8	14, 4	12, 6	1, 64	1, 24	0, 872
	18, 5	16, 0	14, 1	2, 17	1, 69	1, 24
	20, 1	17, 5	15, 5	2, 73	2, 18	1, 65
	21, 7	19, 0	16, 9	3, 33	2, 70	2, 09
	23, 2	20, 5	18, 3	3, 94	3, 25	2, 56
	24, 7	21, 9	19, 7	4, 57	3, 82	3, 05
	26, 2	23, 3	21, 0	5, 23	4, 40	3, 57
	27, 7	24, 7	22, 4	5, 89	5, 01	4, 11
	29, 1	26, 1	23, 7	6, 57	5, 63	4, 66
	30, 6	27, 5	25, 0	7, 26	6, 26	5, 23
	32, 0	28, 8	26, 3	7, 96	6, 91	5, 81
	33, 4	30, 2	27, 6	8, 67	7, 56	6, 41
	34, 8	31, 5	28, 9	9, 39	8, 23	7, 01
	36, 2	32, 9	30, 1	10, 1	8, 91	7, 63
	37, 6	34, 2	31, 4	10, 9	9, 59	8, 26
	38, 9	35, 5	32, 7	11, 6	10, 3	8, 90
	40, 3	36, 8	33, 9	12, 3	11, 0	9, 54
	41, 6	38, 1	35, 2	13, 1	11, 7	10, 2
	43, 0	39, 4	36, 4	13, 8	12, 4	10, 9
	44, 3	40, 6	37, 7	14, 6	13, 1	11, 5
	45, 6	41, 9	38, 9	15, 4	13, 8	12, 2
	47, 0	43, 2	40, 1	16, 2	14, 6	12, 9
	48, 3	44, 5	41, 3	16, 9	15, 3	13, 6
	49, 6	45, 7	42, 6	17, 7	16, 0	14, 3
	50, 9	47, 0	43, 8	18, 5	16, 8	15, 0

Приложение 5

(справочное)

⇐ Предыдущая 1 2 34