Оборотная сторона титульного листа РПУД

РАБОЧАЯ ПРОГРАММА УЧЕБНОЙ ДИСЦИПЛИНЫ

Геометрия и топология

Направление подготовки – 02.03.03 «Математическое обеспечение и администрирование информационных систем» профиль «Технология программирования» Форма подготовки (очная)

курс

семестр

3, 4

лекции

час

практические занятия

час.

лабораторные работы

час.

в том числе с использованием МАО лек.

пр.

лаб.

час.

всего часов аудиторной нагрузки

час.

в том числе с использованием МАО

час.

самостоятельная работа

час

в том числе на подготовку к экзамену

час

контрольные работы (количество)

курсовая работа / курсовой проект

семестр

зачет

семестр

экзамен

3, 4

семестр

Рабочая программа составлена в соответствии с требованиями федерального государственного образовательного стандарта высшего образования, утвержденного приказом Министерства образования и науки РФ от 15 марта 2015 г. № 222

Рабочая программа обсуждена на заседании кафедры

протокол №

от

сентября

2015 г.

Заведующая кафедрой

к.ф.-м.н., профессор Шепелева Р.П.

Составитель (ли):

д.ф.-м.н. Скурихин Е. Е.

Оборотная сторона титульного листа РПУД

I. Рабочая программа пересмотрена на заседании кафедры:

Протокол от «_____» _________________ 20___ г. № ______

Заведующий кафедрой _______________________ __________________

(подпись) (И.О. Фамилия)

II. Рабочая программа пересмотрена на заседании кафедры:

Протокол от «_____» _________________ 20___ г. № ______

Заведующий кафедрой _______________________ __________________

(подпись) (И.О. Фамилия)

ABSTRACT

Bachelor’s degree in 02.03.03 – Software and Administration of Information Systems

Study profile/ Specialization/ Master’s Program “Title” Programming technology

Course title: Geometry and topology

Basic part of Block, credits.

Instructor: Skurikhin E. E.

At the beginning of the course a student should be able to: sustainable use theoretical knowledge practical skills in all areas of mandatory minimum content of the secondary (full) education in mathematics

Learning outcomes:

The ability to use the basic laws of natural sciences in professional activities (СРС-3).

Course description: the basic concepts and tools of geometry, topology, algebra; the basic laws of natural science (math) disciplines.

Main course literature

1. A.G. Kurosh. The course of higher algebra. - St. Petersburg, " Lan", 2011 - 462 p.http: //lib.dvfu.ru: 8080/lib/item? id=chamo: 410558& theme=FEFU

2. A.I.Kostrikin, Y.I. Manin. Linear algebra and geometry. - St. Petersburg, " Lan", 2008 – 303р.

http: //lib.dvfu.ru: 8080/lib/item? id=chamo: 281458& theme=FEFU.

3. AI Maltsev. Fundamentals of linear algebra. - St. Petersburg, " Lan", 2005, - 470р.

http: //lib.dvfu.ru: 8080/lib/item? id=chamo: 239638& theme=FEFU

4. MM Postnikov. Linear algebra. - St. Petersburg, " Lan", 2009, - 400p. http: //e.lanbook.com/view/book/319/

5. DV Beklemishev. Course of analytical geometry and linear algebra. - M.: Nauka, 2005, 308 c.

http: //lib.dvfu.ru: 8080/lib/item? id=chamo: 275482& theme=FEFU

6. D.K.Faddeev, I.S.Sominskii. Problems in higher algebra. - St. Petersburg, " Lan", 2008 - 288 p.

http: //lib.dvfu.ru: 8080/lib/item? id=chamo: 251141& theme=FEFU.

10. Lyubarskii M.G. Vector algebra and its application. Web, 2010 (pdf), 166 р. http: //eqworld.ipmnet.ru/ru/library/books/Lyubarskij2010ru.pdf

Form of final knowledge control: Exam

Аннотация

Рабочая программа учебной дисциплины «Геометрия и топология» разработана для студентов 2 курса по направлению, обучающихся по направлению 02.03.03 «Математическое обеспечение и администрирование информационных систем», профиль «Технология программирования». Общая трудоемкость освоения дисциплины составляет 7 зачетных единиц (252 часа). Дисциплина реализуется на 2 курсе в 3, 4 семестре. В 3 семестре дисциплина содержит 54 часа лекций, 36 часов практических занятий, 0 часов лабораторных работ, из них 0 часов лекций, 0 часов практических занятий, 0 часов лабораторных работ с использованием методов активного обучения. В 4 семестре дисциплина содержит 18 часов лекций, 36 часов практических занятий, 0 часов лабораторных работ, из них 0 часов лекций, 0 часов практических занятий, 0 часов лабораторных работ с использованием методов активного обучения. На самостоятельную работу студентов отводится 108 часов, из них 72 на подготовку к экзамену.

Преподавание геометрии и топологии связано с курсами математического анализа, дифференциальных уравнений, информатики, прикладными дисциплинами. Опирается на школьный курс математики; для усвоения материала необходимо знать факты и формулы и уметь производить алгебраические преобразования в рамках школьного курса математики. Для изучения данной дисциплины необходимо усвоение курса математического анализа в объеме двух семестров, а также разделов курса алгебры, относящихся к линейной алгебре.

Целями освоения дисциплины являются введение в такие современные разделы математики, как алгебраическая и дифференциальная топология, тензорный анализ, а также знакомство с методами, применяющимися в дальнейшем при изучении физики, механики, дифференциальных уравнений, математического анализа.

Задачами изучения дисциплины являются:

- овладение векторной алгеброй в многомерных пространствах и её применениями к геометрическим задачам,

- изучение дифференцируемых кривых и поверхностей,

- овладение методом дифференциальных форм, основными понятиями общей топологии и их связями с математическим анализом и дискретной математикой,

- знакомство с теорией гомологий, либо с теорией гладких многообразий.

В результате освоения дисциплины обучающийся должен знать:

• фундаментальные понятия геометрии и топологии;

• основные методы геометрии и топологии, из связь с алгебраическими и аналитическими методами и их место в других областях науки и техники;

• а также:

• уметь применять свои геометрические знания при решении теоретических и прикладных задач.

• решать основные типы геометрических задач, уметь использовать уравнения линий и поверхностей.

В результате изучения дисциплины у студентов формируются следующие компетенции:

Код и формулировка компетенции	Этапы формирования компетенции
Способность применять в профессиональной деятельности знания математических основ информатики (ОПК-2)	Знает	основные понятия и инструменты геометрии и топологии, роль и место их в математической науке, в приложения к естественным наукам.
Умеет	применять полученные знания для решения математических задач, использовать геометрический язык и символику при построении моделей; применять методы геометрии и топологии.
Владеет	Геометрическими и топологическими методами решения научных, в том числе прикладных задач.

Для формирования вышеуказанных компетенций в рамках дисциплины «Геометрия и топология» применяются следующие методы активного обучения:

Проблемная лекция - опирается на логику последовательно моделируемых проблемных ситуаций путем постановки проблемных вопросов или предъявления проблемных задач

Уровень сложности, характер проблем зависят от подготовленности обучающихся, изучаемой темы и других обстоятельств.

Лекция-консультация. Эта форма занятий предпочтительна при изучении тем с четко выраженной практической направленностью. Варианты проведения подобных лекций:

Вариант 1. Занятия начинаются со вступительной лекции, где преподаватель акцентирует внимание обучающихся на ряде проблем, связанных с практикой применения рассматриваемого положения. Затем слушатели задают вопросы.

Основная часть занятия (до 50% учебного времени) уделяется ответам на вопросы. В конце занятия проводится небольшая дискуссия, свободный обмен мнениями, завершающийся заключительным словом лектора.

Вариант 2. За несколько дней до объявленного занятия преподаватель собирает вопросы слушателей в письменном виде.

Первая часть занятия проводится в виде лекции, в которой преподаватель отвечает на эти вопросы, дополняя и развивая их по своему усмотрению.

Вторая часть проходит в форме ответов на дополнительные вопросы слушателей, свободного обмена мнениями, и завершается заключительным словом преподавателя.

Вариант 3. Слушатели заблаговременно получают материал к занятию. Как правило, он носит не только учебный, но и инструктивный характер, т.е.: представляет собой методическое руководство к практическому использованию.

Слушатели должны изучить материал и подготовить свои вопросы лектору-консультанту. Занятие проводится в форме ответов на вопросы и свободного обмена мнениями

Лекция-беседа. Она предполагает максимальное включение обучающихся в интенсивную беседу с лектором. Преимущество этой формы перед обычной лекцией состоит в том, что она привлекает внимание слушателей к наиболее важным вопросам темы, определяет содержание, методы и темп изложения учебного материала с учетом особенностей аудитории.

. Различают несколько ее разновидностей:

лекция-диалог

лекция-дискуссия,

лекция-диспут.

I. СТРУКТУРА И содержание теоретической части курса

1. Евклидовы пространства и их подпространства. Метод координат. (20 часов)

Измерение расстояний. Метрическое пространство. Отрезки, лучи и прямые. Определение евклидова пространства. Векторы в евклидовом пространстве, векторная алгебра. Векторное параметрическое уравнение прямой, луча, отрезка. Угол между векторами. Скалярное произведение, связь с проекцией. Алгебраические свойства и геометрический смысл скалярного произведения. Параллельные переносы точек, векторов и прямых. Групповые свойства параллельных переносов. Операции над векторами, отложенными от разных точек. Аффинные и декартовы системы координат. Свойства и вычисление декартовых координат, их связь с проекциями, углами и скалярными произведениями.

Подпространства эвклидова пространства. Их характеристика в терминах векторных подпространств. Задание эвклидова подпространства векторным подпространством. Размерность евклидова подпространства. Параллельность векторов и подпространств. Необходимое и достаточное условие пересечения 2 подпространств. Изометрии и преобразования подобия. Их разложения в суперпозицию параллельного переноса и линейного преобразования.

Прямая, как одномерное подпространство евклидова пространства. Каноническое уравнения прямой. Параллельность 2 прямых. Взаимное расположение 2 прямых в произвольном евклидовом пространстве, а также в 2-мерном евклидовом пространстве.

Плоскость, как двумерное евклидово подпространство. Векторное параметрическое уравнение плоскости. Линейная геометрия плоскости. Взаимное расположение 2 прямых, 2 плоскостей, а также прямой и плоскости в многомерных пространствах.

Прямые и плоскости в 3-мерном пространства. Их уравнения и взаимное расположение. Полуплоскость и полупространство. Их задание и свойства.

Векторы в евклидовом пространстве.

Скалярное произведение. Ортогональные системы векторов. Проекция точки на прямую. Формулы для нахождения проекции точки и вектора на прямую. Угол между прямыми. Декартовы системы координат,

Гиперпространства, их задание одним линейным уравнением. Уравнение прямой и плоскости, соответственно в плоскости и 3-мерном пространстве. Линейное уравнение, как уравнение гиперпространства. Проекция точки на евклидово подпространство. Общий перпендикуляр двух подпространств. Формула расстояния от точки до гиперпространства и между параллельными гиперпространствами в n-мерном пространстве. Случаи n=2 и n=3.

Преобразования аффинных и декартовых координат. Матрицы перехода, их свойства. Ориентированные евклидовы пространства. Формулы преобразования аффинных и декартовых координат векторов и точек.

Ориентированные плоскости. Ориентированные углы между векторами плоскости. Формула преобразования декартовых координат на плоскости. Сложение ориентированных углов. Полярные координаты.

Ориентированное трёхмерное пространство. Векторное произведение. Двойное векторное произведение. Тождество Якоби. Понятие алгебры Ли. Смешанное произведение.

2. Кривые и поверхности в евклидовом пространстве (20 часов).

Дифференцирование и интегрирование вектор-функций 1 переменной. Параметризованные кривые в евклидовом пространстве. Задание параметризованных кривых вектор-функциями. Вектор скорости и касательная. Угол между кривыми в точке пересечения. Длина кривой. Естественная параметризация кривой. Формулы Френе. Кривизна и кручение кривой. Базис Френе.

Поверхности в 3-х мерном эвклидовом пространстве. Элементарные области на плоскости. Элементарные поверхности, поверхности, локальные параметризации, дифференцируемые и гладкие параметризации и поверхности. График дифференцируемой функции, как гладкая элементарная поверхность. Локальное представление гладкой поверхности в виде графика функции

Касательное пространство к поверхности. Описание касательного пространства в неособой точке поверхности. Уравнение касательной плоскости и нормальной прямой. Задание квадратичной формы на касательном пространстве. 1-я основная (метрическая) форма поверхности, коэффициенты метрической формы..

2-я основная форма поверхности. Нормальная кривизна кривой на поверхности. Теорема Менье. Теорема Эйлера. Гауссова и средняя кривизны.

Деривационные формулы. Символы Кристоффеля. Теорема Гаусса. Элементы внутренней геометрии поверхностей. Критерий изометричности. Ковариантные производные. Геодезическая кривизна. Геодезические на поверхностях.

Функционал действия. Вывод уравнений Эйлера – Лагранжа. Экстремальные свойства геодезических. Поверхности вращения.

Кривые и поверхности 2 степени. Их исследование, построение и классификация.

Элементы топологии (18 час)

Основные теоретико-множественные операции и соотношения. Определение топологического пространства. Примеры. Метрическая и эвклидова топологии. Аксиомы отделимости. Подпространства топологического пространства.

Открытые и замкнутые множества. Замыкание, внутренность, граница.

База и предбаза топологии. Фундаментальные системы окрестностей.

Непрерывность и пределы отображений. Критерии непрерывности отображений топологических и метрических пространств. Непрерывность суперпозиции и ограничения отображений.

Факторные отображения и гомеоморфизмы. Открытые и замкнутые отображения. Фактортопология и склеивание.

Связность и линейная связность.

Топологические свойства и конструкции. Аксиомы отделимости. Связность, линейная связность, компоненты связности. Связные подмножества вещественной прямой.

Компактные пространства. Произведение топологических пространств. Теоремы Тихонова о произведении и вложении.

Выпуклые множества. Симплексы, грани симплекса. Теорема о гомеоморфности компактного выпуклого множества шару, а его границы - сфере. Описание внутренних точек симплекса. Гомеоморфность симплекса шару. Симплициальные комплексы. Триангуляции и полиэдры. Точные последовательности, комплексы и гомологии. Вычисление групп гомологий симплициального комплекса. Функториальные свойства гомологий. Общее представление о функторах. Гомологические функторы. Теорема о неподвижной точке отображения шара в себя.

V. СПИСОК УЧЕБНОЙ ЛИТЕРАТУРЫ И ИНФОРМАЦИОННО-МЕТОДИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ДИСЦИПЛИНЫ

Основная литература

1. Билинейная геометрия. Евклидовы пространства: [учебное пособие] ч. 1 / Е. Е. Скурихин. Владивосток: Изд-во Дальневосточного университета, 2010. – 78 с. https: //lib.dvfu.ru: 8443/lib/item? id=chamo: 294956& theme=FEFU

2. Билинейная геометрия. Кривые и поверхности второй степени: [учебное пособие] ч. 2 / Е. Е. Скурихин, Н. В. Трикашная. Владивосток: Изд-во Дальневосточного университета, 2010. https: //lib.dvfu.ru: 8443/lib/item? id=chamo: 295056& theme=FEFU

3. Курс геометрии: элементы топологии, дифференциальная геометрия, основания геометрии / В. П. Кузовлев, Н. Г. Подаева. Москва: Физматлит, 2012. -206 с. https: //lib.dvfu.ru: 8443/lib/item? id=chamo: 674834& theme=FEFU

4. Дискретная дифференциальная геометрия. Интегрируемая структура / А. И. Бобенко, Ю. Б. Сурис; пер. с англ. В. Э. Адлера. Москва Ижевск: Регулярная и хаотическая динамика: Институт компьютерных исследований, 2010. – 487 с. https: //lib.dvfu.ru: 8443/lib/item? id=chamo: 299194& theme=FEFU

5. А.И. Кострикин, Ю.И. Манин. Линейная алгебра и геометрия. – Санкт-Петербург, «Лань», 2008, – 303 с. http: //lib.dvfu.ru: 8080/lib/item? id=chamo: 281458& theme=FEFU

6. Шафаревич, И. Р. Линейная алгебра и геометрия [Электронный ресурс] / И. Р. Шафаревич, А. О. Ремизов. - М.: ФИЗМАТЛИТ, 2009. - 512 с. - ISBN 978-5-9221-1139-3. http: //znanium.com/catalog.php? bookinfo=544772

7. Лекции по дифференциальной геометрии. [Электронный ресурс] / Сизый С. В. - М.: ФИЗМАТЛИТ, 2007. – 376 c. http: //www.studentlibrary.ru/book/ISBN9785922107426.html

8. Примаков, Д. А. Геометрия и топология [Электронный ресурс]: учеб. пособие / Д. А. Примаков, Р. Я. Хамидуллин. - 2-е изд., перераб. и доп. - М.: МФПА, 2011. - 272 с. (Университетская серия). - ISBN 978-5-902597-13-1. http: //znanium.com/catalog.php? bookinfo=451172

9. Курс аналитической геометрии и линейной алгебры [Электронный ресурс]: Учеб. для вузов. / Беклемишев Д. В. - 12-е изд., испр. - М.: ФИЗМАТЛИТ, 2009. - http: //www.studentlibrary.ru/book/ISBN9785922109796.html

Дополнительная литература

1. Иванов А.О., Тужилин А.А. Лекции по классической дифференциальной геометрии. М.: Новая университетская библиотека. – 2009.- 233 с.

2. Прасолов В.В., Тихомиров В.М. Геометрия. 2-е изд., перераб. И доп. – М.: МЦНМО. – 2007.- 328 с.

3. Босс В. Лекции по математике. Том 13. Топология: Учебное пособие. – М.: Книжный дом «ЛИБРОКОМ». – 2009. – 216 с.

4. Новиков С.П., Фоменко А.Т. Элементы дифференциальной геометрии и топологии. M.: Наука, физ.-мат., 1987. 432 с.

5. Постников М.М. Лекции по геометрии. Семестр III. M.: Наука, физ.-мат., 1986. 480 с.

6. Погорелов А.В. Дифференциальная геометрия. М.: Наука, физ.-мат., 1974. 176 с.

7. Общая топология / Дж. Л. Келли; пер. с англ. А. В. Архангельского. М.: Наука, 1981. 432 с. https: //lib.dvfu.ru: 8443/lib/item? id=chamo: 691627& theme=FEFU

8. Сборник задач по дифференциальной геометрии. Под ред. А.С.Феденко. М.: Наука, физ.-мат., 1979. 272 с.

9. Дубровин Б.А., Новиков С.П., Фоменко А.Т. Современная геометрия. M.: Наука, физ.-мат., 1986. 760 с.

10. Дубровин Б.А., Новиков С.П., Фоменко А.Т. Современная геометрия. Методы теории гомологий. M.: Наука, физ.-мат., 1984. 344 с.

11. Дубровин Б.А., Новиков С.П., Фоменко А.Т. Современная геометрия: Методы и приложения. В 3-х томах. - М.: УРСС – 1998-2001.

12. Новиков С.П. Топология. М.: Институт компьютерных исследований. – 2002. – 335 с. https: //lib.dvfu.ru: 8443/lib/item? id=chamo: 406295& theme=FEFU

13. Общая топология / Р. Энгелькинг; пер. с англ. М. Я. Антоновского, А. В. Архангельского. М.: Мир. 1986. – 751 с. https: //lib.dvfu.ru: 8443/lib/item? id=chamo: 53165& theme=FEFU

14. Постников М.М. Лекции по геометрии. Семестр II. М.: Наука, физ.-мат. 1986. 400 с.

15. Хилтон П. Дж., Уайли С. Теория гомологий. М.: Мир. 1966. 452 с. https: //lib.dvfu.ru: 8443/lib/item? id=chamo: 94649& theme=FEFU

16. Элементы теории гомологий / В. В. Прасолов. Москва: Изд-во Московского центра непрерывного математического образования, 2006. – 448 с. https: //lib.dvfu.ru: 8443/lib/item? id=chamo: 248888& theme=FEFU

17. Сборник задач по аналитической геометрии: учебное пособие / Д. В. Клетеник; под ред. Н. В. Ефимова. Санкт-Петербург: Лань, 2010. – 223 с. https: //lib.dvfu.ru: 8443/lib/item? id=chamo: 307475& theme=FEFU

18. А.И. Мальцев. Основы линейной алгебры. – Санкт-Петербург, «Лань», 2005, - 470 с. http: //lib.dvfu.ru: 8080/lib/item? id=chamo: 239638& theme=FEFU

19. Курс аналитической геометрии и линейной алгебры: учебник / П. С. Александров. Санкт-Петербург, «Лань», 2009, - 512 с. http: //lib.dvfu.ru: 8080/lib/item? id=chamo: 298699& theme=FEFU

Интернет-ресурсы

1. http: //www.studentlibrary.ru/book/ISBN9785922113601.html Курс геометрии: элементы топологии, дифференциальная геометрия, основания геометрии [Электронный ресурс] / Кузовлев В.П., Подаева Н.Г. - М.: ФИЗМАТЛИТ, 2012. -

2. http: //www.studentlibrary.ru/book/ISBN9785922111393.html Линейная алгебра и геометрия. [Электронный ресурс] / Шафаревич И.Р., Ремизов А.О. - М.: ФИЗМАТЛИТ, 2009. -

3. http: //www.studentlibrary.ru/book/ISBN9785922115827.html Высшая математика. Линейная алгебра ианалитическая геометрия [Электронный ресурс] / Геворкян П.С - М.: ФИЗМАТЛИТ, 2014. -

4. http: //www.studentlibrary.ru/book/ISBN5922102672.html Высшая геометрия. [Электронный ресурс] / Ефимов Н.В. - 7-е изд. - М.: ФИЗМАТЛИТ, 2004. -

5. http: //www.studentlibrary.ru/book/ISBN9785922112901.html Аналитическая геометрия и линейная алгебра. [Электронный ресурс] / Кадомцев С. Б. - 2-е изд., испр. и доп. - М.: ФИЗМАТЛИТ, 2011. -

6. http: //www.studentlibrary.ru/book/ISBN5922103865.html Линейная алгебра и многомерная геометрия [Электронный ресурс] / Ефимов Н.В., Розендорн Э.Р. - 4-е изд. - М.: ФИЗМАТЛИТ, 2005. -

7. http: //znanium.com/catalog.php? bookinfo=544579 Высшая геометрия / Н.В. Ефимов, - 7-е изд. - М.: ФИЗМАТЛИТ, 2004. - 584 с. ISBN 5-9221-0267-2

8. http: //znanium.com/catalog.php? bookinfo=318084 Основы линейной алгебры и аналитической геометрии: Учебно-методическое пособие / В.Г. Шершнев. - М.: НИЦ ИНФРА-М, 2013. - 168 с.: 60x88 1/16. - (Высшее образование: Бакалавриат). (обложка) ISBN 978-5-16-005479-7

9. http: //www.studentlibrary.ru/book/ISBN5922100106.html Сборник задач по аналитической геометрии и линейной алгебре [Электронный ресурс]: Учеб. пособие / Беклемишева Л.А., Петрович А.Ю., Чубаров И.А.; Под ред. Д.В. Беклемишева. - 2-е изд., перераб. - М.: ФИЗМАТЛИТ, 2006." -

10. http: //www.studentlibrary.ru/book/ISBN9785922114806.htmlРешение задач из курса аналитической геометрии и линейной алгебры [Электронный ресурс] / Беклемишев Д.В. - М.: ФИЗМАТЛИТ, 2014. -

11. http: //www.alleng.ru/edu/math9.htm Образовательные ресурсы Интернета - математика. Высшая школа.

12. https: //mipt.ru/education/chair/mathematics/upload/ff4/Umnov-AnGeom-i-LinAl-arph0duocc9.pdf Аналитическая геометрия и линейная алгебра: учеб. пособие / А. E. Умнов. – 3-е изд., испр. и доп. –. М.: МФТИ, 2011. – 544 с. ISBN 978-5-7417-0378-6.

13. http: //lanbook.com/books/element.php? pl1_cid=42& pl1_id=207 А.И. Кострикин, Ю.И. Манин. Линейная алгебра и геометрия. – Санкт-Петербург, «Лань», 2008, – 303 с.

14. http: //lanbook.com/books/element.php? pl1_cid=42& pl1_id=493 П.С. Александров. Курс аналитической геометрии и линейной алгебры. Санкт-Петербург, «Лань», 2009, - 512 с.

15. http: //www.alleng.ru/d/math/math156.htm Клетеник Д.В. Сборник задач по аналитической геометрии.1980. – 240 с.

16. http: //e.lanbook.com/view/book/319/ М.М. Постников. Линейная алгебра. Лекции по геометрии. Часть II: Учебное пособие – Санкт-Петербург, «Лань», 2009. - 400 с.

VI. МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ОСВОЕНИЮ ДИСЦИПЛИНЫ

Для успешного достижения учебных целей занятий должны выполняться следующие основные требования:

-соответствие действий обучающихся ранее изученным на лекционных и семинарских занятиях методикам и методам.

-максимальное приближение действий студентов к реальным, соответствующим будущим функциональным обязанностям.

-поэтапное формирование умений и навыков, т.е. движение от знаний к умениям и навыкам, от простого к сложному и т.д..

-использование при работе на тренажерах или действующей технике фактических документов, технологических карт, бланков и т.п.

-выработка индивидуальных и коллективных умений и навыков.

- распределение времени, отведенного на занятие, на решение каждой задачи;

-подбор иллюстративного материала (графиков, таблиц, схем), необходимого для решения задач, продумывание расположения рисунков и записей на доске.

Студент должен:

- научиться работать с книгой, документацией и схемами, пользоваться справочной и научной литературой.

-формировать умение учиться самостоятельно, т.е. овладевать методами, способами и приемами самообучения, саморазвития и самоконтроля.

. На лекциях преподаватель объясняет теоретический материал. Вводит основные понятия, определения, свойства. Формулирует и доказывает теоремы. Приводит примеры. Необходимо поддерживать непрерывный контакт с аудиторией, отвечать на возникающие у студентов вопросы. На практических занятиях преподаватель разбирает примеры по пройденной теме. Во второй части занятия студентам предлагается работать самостоятельно, выполняя задания по теме. Преподаватель контролирует работу студентов, отвечает на возникающие вопросы, подсказывает ход и метод решения. Если знаний полученных в аудитории оказалось недостаточно, студент может самостоятельно повторно прочитать лекцию, просмотреть практикум с разобранными примерами, которые собраны в изучаемом курсе в системе Bb dvfu. После выполнения задания, студент отправляет его на проверку преподавателю в соответствующем «Назначении». Работа должна быть отослана в формате PDF одним документом. По данному курсу разработаны методические указания, которые выложены с системе Bb dvfu в соответствующем разделе.

По данному курсу разработаны следующие методические пособия:

1. Билинейная геометрия. Евклидовы пространства: [учебное пособие] ч. 1 / Е. Е. Скурихин. Владивосток: Изд-во Дальневосточного университета, 2010. – 78 с. http: //srv-elib-01.dvfu.ru: 8000/cgi-bin/edocget.cgi? ref=/514/skurikhin2.pdf

.Содержание пособия:

1. Векторы в евклидовых пространствах

1.0. Функция сравнения удалённостей.

1.1. Взаимное расположение точек на прямой

1.2. Операции над векторами.

1.3. Свойства ортогональных проекций.

1.4. Скалярное произведение векторов.

1.5. Операции над свободными векторами.

1.6. Параллельные переносы

2. Евклидовы подпространства и системы координат.

2.0. Необходимые сведения из линейной алгебры.

2.1. Общие свойства евклидовых подпространств.

2.2. Аффинные и декартовы системы координат.

2. Билинейная геометрия. Кривые и поверхности второй степени [Электронный ресурс]: [учебное пособие] ч. 2 / Е. Е. Скурихин, Н. В. Трикашная. http: //srv-elib-01.dvfu.ru: 8000/cgi-bin/edocget.cgi? ref=/514/skurikhin1.pdf

Содержание пособия:

1. Уравнения эллипса

2. Уравнения гиперболы

3. Классификация кривых

VII. МАТЕРИАЛЬНО-ТЕХНИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ДИСЦИПЛИНЫ

Учебные аудитории кампуса ДВФУ. Мультимедийная лекционная аудитория (мультимедийный проектор, настенный экран, документ-камера)

Приложение 1

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное автономное образовательное учреждение

высшего образования

«Дальневосточный федеральный университет»

(ДВФУ)

ШКОЛА ЕСТЕСТВЕННЫХ НАУК

УЧЕБНО-МЕТОДИЧЕСКОЕ ОБЕСПЕЧЕНИЕ САМОСТОЯТЕЛЬНОЙ РАБОТЫ ОБУЧАЮЩИХСЯ

по дисциплине «Геометрия и топология»

Направление подготовки – 02.03.03 «Математическое обеспечение и администрирование информационных систем»

профиль «Технология программирования»

Форма подготовки (очная)

Владивосток

План-график выполнения самостоятельной работы по дисциплине

№ п/п	Дата/сроки выполнения	Вид самостоятельной работы	Примерные нормы времени на выполнение	Форма контроля
	1-4 недели	Контрольная работа	1 пара	Зачет по заданию
	5-6 недели	Индивидуальное задание	1 неделя	Зачет по заданию
	7-8 недели	Индивидуальное задание	1 неделя	Зачет по заданию
	9-10 недели	Контрольная работа	1 пара	Зачет по заданию
	11-14 недели	Индивидуальное задание	2 недели	Зачет по заданию
	15-17 недели	Индивидуальное задание	2 недели	Зачет по заданию
	19 неделя	Контрольная работа	1 неделя	Зачет по заданию
	20-22 недели	Индивидуальное задание	1 неделя	Зачет по заданию
	23-29 недели	Индивидуальное задание	2 недели	Зачет по заданию

Материалы для самостоятельной работы студентов подготовлены в виде индивидуальных домашних заданий и контрольных работ по каждой теме (образцы типовых ИДЗ представлены ниже). Критерии оценки: студент получает максимальный балл, если работа выполнена без ошибок и оформлена в соответствии с требованиями преподавателя.

Индивидуальное задание № 1 (системы)

Индивидуальное задание № 2 (прямая и плоскость)

Вариант № 1

1. Найти уравнение плоскости, параллельной оси Oz и проходящей через точки A(2; 3; -1) и В (-1; 2; 4).

2. Общие уравнения прямой преобразовать к каноническому виду.

3. Составить уравнение плоскости, проходящей через прямую x=3t+1, y=2t+3, z= –t–2 параллельно прямой , .

Вариант № 2

1. Найти уравнение плоскости, проходящей через точки A(2; -3; 2) и B(7; 1; 0) и параллельной оси Ох.

2. Уравнения прямой преобразовать к каноническому виду и определить углы, образуемые этой прямой с координатными осями.

3. Составить уравнение плоскости, проходящей через прямую перпендикулярно к плоскости .

Вариант № 3

1. Найти уравнение плоскости, параллельной оси Оу и проходящей через точки А(2; 1; -2) и В(-7; -2; 1).

2. Привести к каноническому виду Общие уравнения прямой

3. Составить уравнение плоскости, проходящей через точку М₁(1; 2; -3) параллельно прямым , .

Вариант № 4

1. Найти уравнение плоскости, параллельной плоскости хОу и проходящей через точку A (1; 2; -4).

2. Преобразовать к каноническому виду общие уравнения прямой

3. Составить уравнение плоскости, проходящей через точку М₀(1; -2; 1) перпендикулярно к прямой , .

Вариант № 5

1. Составить уравнение плоскости, перпендикулярной оси Ох и проходящей через точку А (3; 7; -1).

2. Найти уравнения плоскостей, проектирующих прямую на координатные плоскости.

3. Убедившись, что прямые , , параллельны, вычислить расстояние d между ними.

Вариант № 6

1. Найти уравнение плоскости, параллельной плоскости xOz и проходящей через точку A(2; -3; 4).

3. Найти точку Q, симметричную точке Р(4; 1; 6) относительно прямой , .

Вариант № 7

1. Составить уравнение плоскости, проходящей через ось Ох и точку А (2; 1; 3).

2. Определить следы прямой

на координатных плоскостях (следом прямой на плоскости называется точка пересечения прямой с плоскостью).

3. Найти точку пересечения прямой и плоскости:

, .

Вариант № 8

1. Найти уравнение плоскости, проходящей через ось Oz и точку А (-2; 4; -4).

2. Найти координаты следов прямой 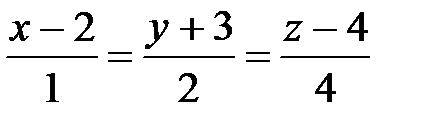на координатных плоскостях (следом прямой на плоскости называется точка пересечения прямой с плоскостью).

3. Найти точку пересечения прямой и плоскости:

, .

Вариант № 9

1.. Найти уравнение плоскости, проходящей через точку A(2; -5; 4) и через ось Оу.

2. Найти острый угол между прямыми и

3. Найти точку пересечения прямой и плоскости:

, .

Вариант № 10

1. Какие отрезки на координатных осях отсекает плоскость 2х + 3у - 5z + 30 = 0?

2. Через точку А(1; -1; 2) провести прямую, параллельную прямой .

3. Доказать, что прямая x=3t-2, y=–4t+1, z=4t–5 параллельна плоскости .

Вариант № 11

1. Найти величины отрезков, отсекаемых плоскостью на координатных осях.

2. Через точку (2; -1; 3) провести прямую, параллельную оси Ох.

3. При каком значении С прямая , , параллельна плоскости ?

Вариант № 12

1. Найти расстояние между параллельными плоскостями

; .

2. Найти уравнения прямой, проходящей через точки A(1; 2; -1) и B(0; 3; -4).

3. Найти точку Q, симметричную точке Р(2; -5; 7) относительно прямой, проходящей через точки М₁(5; 4; 6) и М₂(-2; -17; -8).

Вариант № 13

1.Найти расстояние между параллельными плоскостями ; .

2. Найти уравнения прямой, проходящей через точки А (3; 0; 4) и В (-1; -2; 3).

3. Вычислить расстояние d точки Р(1; -1; -2) от прямой .

Вариант № 14

1. Через точку M(2; 3; -1) провести плоскость, параллельную плоскости .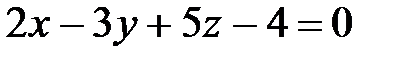

2. Найти острый угол между прямой и плоскостью .

3. Вычислить расстояние d от точки Р(2; 3; -1) до прямой .

12 Следующая ⇒