Лекция 3. Непрерывность функции. Точки разрыва.
Опр. Пусть функция  определена в некоторой окрестности точки
определена в некоторой окрестности точки 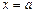 . Функция
. Функция  называется непрерывной в точке а, если
называется непрерывной в точке а, если
 . (1)
. (1)
Равенство (1) означает выполнение трех условий:
1) функция  определена в точке
определена в точке 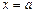 и в некоторой ее окрестности;
и в некоторой ее окрестности;
2) функция  имеет предел при
имеет предел при  ;
;
3) предел функции  в точке а равен значению функции в этой точке.
в точке а равен значению функции в этой точке.
Так как  , то равенство (1) можно записать в виде
, то равенство (1) можно записать в виде
 .
.
Это означает, что при нахождении предела непрерывной функции  можно перейти к пределу под знаком функции, т.е. в функцию
можно перейти к пределу под знаком функции, т.е. в функцию  вместо аргумента
вместо аргумента  подставить его предельное значение.
подставить его предельное значение.
Например,  .
.
Опр. Если  , то функция
, то функция  называется непрерывной в точке а справа; если
называется непрерывной в точке а справа; если  , то – непрерывной в точке а слева.
, то – непрерывной в точке а слева.
На основании изложенного заключаем: для того, чтобы функция  была непрерывной в точке а, необходимо и достаточно, чтобы она была непрерывной в этой точке справа и слева.
была непрерывной в точке а, необходимо и достаточно, чтобы она была непрерывной в этой точке справа и слева.
Приведем еще одно определение функции, непрерывной в точке 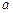 .
.
Равенство (1) равносильно следующему: 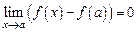 .
.
Если учесть, что соотношения  и
и  также равносильны, то получим, что условие непрерывности функции
также равносильны, то получим, что условие непрерывности функции  в точке а запишется в виде
в точке а запишется в виде
 . (2)
. (2)
Опр. Разность  называют приращением независимой переменной
называют приращением независимой переменной  в точке а и обозначают через
в точке а и обозначают через  , а разность
, а разность  – приращением функции
– приращением функции  в точке а и обозначают
в точке а и обозначают  . Теперь условие (2) можно записать так:
. Теперь условие (2) можно записать так:
 . (3)
. (3)
Заметим здесь, что  и
и  .
.
Тогда новое определение непрерывности функции в точке 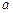 будет следующим.
будет следующим.
Опр. Функция  называется непрерывной в точке а, если ее приращение в этой точке есть бесконечно малая функция.
называется непрерывной в точке а, если ее приращение в этой точке есть бесконечно малая функция.
 Геометрический смысл этого определения показан на рис.1.
Геометрический смысл этого определения показан на рис.1.
Пример 1. Исследовать на непрерывность функцию  .
.
Решение. Функция  определена при всех
определена при всех  . Возьмем произвольную точку
. Возьмем произвольную точку  и найдем приращение
и найдем приращение  :
: 
 .
.
Тогда  .
.
Согласно определению (3), функция  непрерывна в любой точке
непрерывна в любой точке  . □
. □
Опр. Функция  называется непрерывной на интервале
называется непрерывной на интервале  , если она непрерывна в каждой точке
, если она непрерывна в каждой точке  . Если же, кроме того, функция
. Если же, кроме того, функция  непрерывна в точке а справа, а в точке
непрерывна в точке а справа, а в точке  – слева, то функция
– слева, то функция  называется непрерывной на отрезке
называется непрерывной на отрезке  .
.
Опр. Функция  называется кусочно-непрерывной на отрезке
называется кусочно-непрерывной на отрезке  , если она непрерывна во всех внутренних точках
, если она непрерывна во всех внутренних точках  , за исключением конечного числа точек, в которых она имеет разрывы первого рода, а в точках а и
, за исключением конечного числа точек, в которых она имеет разрывы первого рода, а в точках а и  имеет соответствующие односторонние пределы.
имеет соответствующие односторонние пределы.
Опр. Точка а называется точкой разрыва функции  , если функция
, если функция  не является непрерывной в этой точке.
не является непрерывной в этой точке.
Если 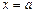 – точка разрыва функции
– точка разрыва функции  , то в ней не выполняется, по крайней мере, одно из условий первого определения непрерывности функции, а именно:
, то в ней не выполняется, по крайней мере, одно из условий первого определения непрерывности функции, а именно:
1. Функция определена в некоторой окрестности точки а, но не определена в самой точке а.
Например, функция 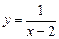 не определена в точке
не определена в точке 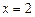 (рис. 2).
(рис. 2).
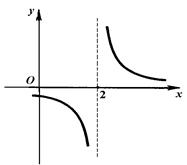 Рис. 2
Рис. 2
| 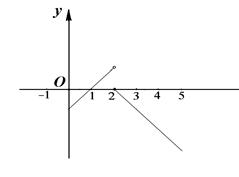 Рис. 3
Рис. 3
|
2. Функция определена в точке а и ее окрестности, но не существует предела  при
при  .
.
Например, функция
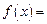
 (3)
(3)
определена в точке 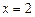
 , однако в точке
, однако в точке 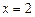 имеет разрыв (рис. 3), т. к. эта функция не имеет предела в этой точке:
имеет разрыв (рис. 3), т. к. эта функция не имеет предела в этой точке:
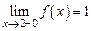 , а
, а 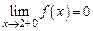 .
.
3. Функция определена в точке а и ее окрестности и существует  .
.
Например, рассмотрим функцию (рис. 4)
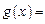
 (4)
(4)

Рис. 4
Здесь  – точка разрыва функции
– точка разрыва функции  , т.к.
, т.к.  а
а  .
.
Все точки разрыва функции разделяются на точки разрыва первого и второго рода.
Опр. Точка а называется точкой разрыва первого рода функции  , если в этой точке существуют конечные пределы функции слева и справа, т.е.
, если в этой точке существуют конечные пределы функции слева и справа, т.е.  и
и  . При этом:
. При этом:
а) если 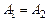 , то точка а называется точкой устранимого разрыва;
, то точка а называется точкой устранимого разрыва;
б) если  , то точка а называется точкой конечного разрыва. Величину
, то точка а называется точкой конечного разрыва. Величину 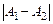 называют скачком функции в точке разрыва
называют скачком функции в точке разрыва 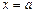 .
.
Опр. Точка а называется точкой разрыва второго рода функции  , если по крайней мере один из односторонних пределов (слева или справа) не существует.
, если по крайней мере один из односторонних пределов (слева или справа) не существует.
Так, функция 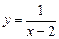 (рис. 2) имеет разрыв второго рода в точке
(рис. 2) имеет разрыв второго рода в точке 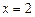 . Для функции (3) (рис. 4) точка
. Для функции (3) (рис. 4) точка 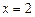 является точкой разрыва первого рода со скачком, равным
является точкой разрыва первого рода со скачком, равным  . Точка
. Точка  является точкой разрыва первого рода для функции (4) (рис. 5). Положив
является точкой разрыва первого рода для функции (4) (рис. 5). Положив  (вместо
(вместо  ) при
) при  , разрыв устранится, функция станет непрерывной в точке
, разрыв устранится, функция станет непрерывной в точке  .
.
Лекция 4. Понятие производной функции. Правила дифференцирования. Таблица производных.
Пусть функция  определена и непрерывна в окрестности точки
определена и непрерывна в окрестности точки 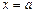 . Если независимой переменной х придать приращение Dх в этой точке, то функция получит соответствующее приращение
. Если независимой переменной х придать приращение Dх в этой точке, то функция получит соответствующее приращение  . Если Dх®0, то, по определению непрерывной в точке
. Если Dх®0, то, по определению непрерывной в точке 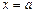 функции, и Dу®0 .
функции, и Dу®0 .
С целью исследования скорости изменения значений функции вводится понятие производной, одного из важнейших понятий математики.
Опр. Производной функции  в точке
в точке 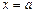 называется предел отношения приращения функции в этой точке к приращению аргумента при стремлении последнего к нулю.
называется предел отношения приращения функции в этой точке к приращению аргумента при стремлении последнего к нулю.
Для обозначения производной используются символы:  . Таким образом, по определению
. Таким образом, по определению
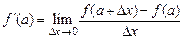 . (1)
. (1)
Операцию нахождения производной называют дифференцированием.
Если функция  имеет производную
имеет производную  в каждой точке
в каждой точке 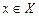 , то производную
, то производную  можно рассматривать как функцию переменной х на множестве X.
можно рассматривать как функцию переменной х на множестве X.
Из определения производной следует и способ ее вычисления.
Пример 1. Найти производную функции  в точке
в точке 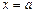 .
.
Решение. Придадим приращение Dх аргументу  в точке
в точке 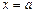 . Найдем соответствующее приращение Dу функции
. Найдем соответствующее приращение Dу функции  :
:
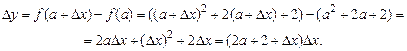
Воспользуемся формулой (1):
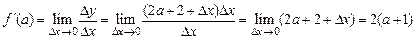 .
.
Таким образом,  . □
. □
Теорема 1. Если функция  в точке х имеет производную
в точке х имеет производную  , то она непрерывна в этой точке.
, то она непрерывна в этой точке.

Популярное:

