Понятие дифференцируемости функции в точке.
Опр. Функция  называется дифференцируемой в точке x, если ее приращение
называется дифференцируемой в точке x, если ее приращение  y в этой точке можно представить в виде
y в этой точке можно представить в виде
 , (1)
, (1)
где А – некоторое число, не зависящее от 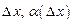 – бесконечно малая функция при
– бесконечно малая функция при  .
.
Теорема 1. Для того, чтобы функция  была дифференцируемой в точке x необходимо и достаточно, чтобы она имела в этой точке производную
была дифференцируемой в точке x необходимо и достаточно, чтобы она имела в этой точке производную  .
.
Дифференциал функции.
Пусть функция  дифференцируема в точке
дифференцируема в точке  . Тогда приращение функции в этой точке может быть записано по формуле (1), где
. Тогда приращение функции в этой точке может быть записано по формуле (1), где  . Так как
. Так как 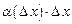 является бесконечно малой функцией более высокого порядка по сравнению c
является бесконечно малой функцией более высокого порядка по сравнению c  (при условии, что
(при условии, что  ), то
), то  . Поэтому первое слагаемое
. Поэтому первое слагаемое  является главной частью приращения
является главной частью приращения  , линейной относительно
, линейной относительно  .
.
Главная часть приращения функции  в точке x, линейная относительно
в точке x, линейная относительно  , называется дифференциалом функции
, называется дифференциалом функции  в этой точке. Для обозначения дифференциала используется обозначение
в этой точке. Для обозначения дифференциала используется обозначение  , а поскольку
, а поскольку  , то
, то
 . (2)
. (2)
Если  , то
, то  не является, вообще говоря, главной частью приращения
не является, вообще говоря, главной частью приращения  . В этом случае, по определению,
. В этом случае, по определению,  .
.
Геометрический смысл дифференциала. Для выяснения геометрического смысла дифференциала проведем к графику функции  в точке
в точке  касательную МТ (рис.1) и обозначим через
касательную МТ (рис.1) и обозначим через  угол ее наклона к положительному направлению оси
угол ее наклона к положительному направлению оси  .
.

Поскольку  , то
, то  . Поэтому из треугольника MLN следует, что дифференциал dy есть приращение ординаты точки касания, соответствующее приращению аргумента
. Поэтому из треугольника MLN следует, что дифференциал dy есть приращение ординаты точки касания, соответствующее приращению аргумента  .
.
Из обозначения производной функции  или
или  видно, что производная функции
видно, что производная функции  равна отношению дифференциала этой функции к дифференциалу аргумента.
равна отношению дифференциала этой функции к дифференциалу аргумента.
Механический смысл дифференциала.
Рассмотрим неравномерное прямолинейное движение точки по закону  , где
, где 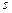 – длина пути, t – время. Пусть
– длина пути, t – время. Пусть 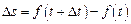 выражает истинное приращение пути за промежуток времени
выражает истинное приращение пути за промежуток времени 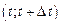 .
.
Вычислим дифференциал пути. Так как  – скорость в момент t, то
– скорость в момент t, то  , т. е.
, т. е. 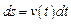 .
.
Таким образом, дифференциал пути равен приращению пути, полученному в предположении, что, начиная с рассматриваемого момента времени t, точка движется равномерно, сохраняя приобретенную скорость.
Инвариантность формы дифференциала.
Найдем дифференциал сложной функции. Пусть  , где
, где  , причем
, причем  имеет производную по u, а
имеет производную по u, а 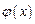 – по x. Тогда, по правилу дифференцирования сложной функции, получаем
– по x. Тогда, по правилу дифференцирования сложной функции, получаем
 .
.
Значит,  . Поскольку
. Поскольку 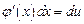 , то
, то  .
.
Таким образом, форма записи дифференциала не зависит от того, является аргумент независимой переменной или функцией другого аргумента. Это свойство дифференциала называют инвариантностью формы дифференциала.
Пример 1. Найти дифференциал сложной функции
 .
.
Решение.
Имеем 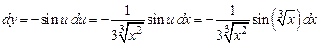 . □
. □
Таблица дифференциалов. Согласно формуле (2), можно из таблицы производных получить аналогичную таблицу для дифференциалов. Так, из формулы  , умножив обе части на
, умножив обе части на 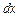 , будем иметь:
, будем иметь:
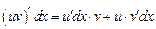 , или
, или  и т. д.
и т. д.
Теорема Ферма. Пусть функция f определена на интервале  и в некоторой точке
и в некоторой точке 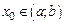 имеет локальный экстремум. Тогда, если в точке
имеет локальный экстремум. Тогда, если в точке 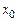 существует производная, то она равна нулю, т.е.
существует производная, то она равна нулю, т.е.  .
.
Теорема Ролля. Пусть функция f непрерывна на отрезке 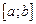 , дифференцируема на интервале
, дифференцируема на интервале  и на концах отрезка
и на концах отрезка 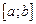 принимает равные значения, то есть
принимает равные значения, то есть  . Тогда существует точка
. Тогда существует точка 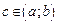 , в которой
, в которой  .
.
Теорема Лагранжа. Если функция f непрерывна на отрезке 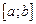 , дифференцируема на интервале
, дифференцируема на интервале  , то существует точка
, то существует точка  , такая, что справедлива формула:
, такая, что справедлива формула:
 .
.
Теорема Коши. Если функции f и g непрерывны на отрезке 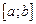 , дифференцируемы на интервале
, дифференцируемы на интервале  , причем
, причем  , то существует точка
, то существует точка 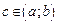 , такая, что справедливо равенство
, такая, что справедливо равенство 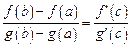 .
.
Теорема 1 (правило Лопиталя). Пусть функции  и
и  непрерывны и дифференцируемы в окрестности точки
непрерывны и дифференцируемы в окрестности точки 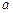 , за исключением, быть может, точки а;
, за исключением, быть может, точки а;  и
и  в указанной окрестности. Тогда, если существует
в указанной окрестности. Тогда, если существует  , то существует также и
, то существует также и  , причем
, причем
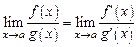 .
.
Лекция 7. Понятие первообразной функции и неопределенный интеграл.
Первообразная функция.
Основной операцией дифференциального исчисления является отыскание производной заданной функции. Однако возникает вопрос о существовании операции, обратной дифференцированию.
Восстановление функции по известной производной этой функции есть одна из основных задач интегрального исчисления.
Опр. Функция  называется первообразной для функции
называется первообразной для функции  на некотором промежутке X, если
на некотором промежутке X, если  :
:  .
.
Например, функция  является первообразной для функции
является первообразной для функции  , так как
, так как  .
.
Функция  является первообразной для функции
является первообразной для функции  на т.к.
на т.к.  .
.
Задача об отыскании первообразной по данной функции  решается неоднозначно. Если, например,
решается неоднозначно. Если, например, 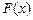 есть первообразная для функции
есть первообразная для функции  , то функция
, то функция  также является первообразной для функции
также является первообразной для функции  . Действительно,
. Действительно, 
 . В частности, функция
. В частности, функция  , где C – произвольная постоянная, есть первообразная для функции
, где C – произвольная постоянная, есть первообразная для функции  .
.
Утверждение 1. Если  и
и  – две первообразные для функции
– две первообразные для функции  на промежутке X, то они отличаются лишь на постоянную, т.е.
на промежутке X, то они отличаются лишь на постоянную, т.е.  где
где 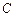 – некоторая постоянная.
– некоторая постоянная.
Другими словами, если  есть первообразная для функции
есть первообразная для функции 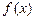 , то множество функций
, то множество функций  включает все первообразные для данной функции
включает все первообразные для данной функции  .
.
Замечание 1. Ранее было показано, что не все функции, заданные на каком-либо интервале  имеют производную. Аналогично, не всякая функция имеет первообразную.
имеют производную. Аналогично, не всякая функция имеет первообразную.
Рассмотрим, например, функцию

Эта функция определена на интервале  и не может являться производной какой-либо функции
и не может являться производной какой-либо функции  на
на  , т.к. по теореме Дарбу производная принимает все свои промежуточные значения, а
, т.к. по теореме Дарбу производная принимает все свои промежуточные значения, а  – всего три значения: 2, 3, 4.
– всего три значения: 2, 3, 4.
Неопределенный интеграл.
Опр. Множество всех первообразных функции  называется неопределенным интегралом функции
называется неопределенным интегралом функции  и обозначается
и обозначается
 .
.
Функция  называется подынтегральной функцией,
называется подынтегральной функцией,  – подынтегральным выражением, переменная x – переменной интегрирования.
– подынтегральным выражением, переменная x – переменной интегрирования.
Итак, если  - первообразная функции
- первообразная функции  на промежутке X, то
на промежутке X, то  , где С – произвольная постоянная.
, где С – произвольная постоянная.
Подчеркнем, что символ  обозначает совокупность всех первообразных для функции
обозначает совокупность всех первообразных для функции  . Отыскание неопределенного интеграла по известной подынтегральной функции называется интегрированием этой функции.
. Отыскание неопределенного интеграла по известной подынтегральной функции называется интегрированием этой функции.
Пример 1. Найти следующие интегралы:
а) 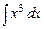 , б)
, б) 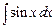 , в)
, в)  .
.
Решение. Воспользовавшись таблицей производных, имеем:
а)  , б)
, б)  , в)
, в)  ,
,
т. к. 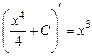 ,
,  ,
,  . □
. □
Свойства неопределенного интеграла.
1) Если функция 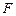 дифференцируема на некотором промежутке, то на нем
дифференцируема на некотором промежутке, то на нем

или, что то же самое,
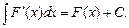
Это сразу следует из определения неопределенного интеграла как совокупности всех дифференцируемых функций, дифференциал которых стоит под знаком интеграла.
2) Пусть функция 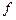 имеет первообразную на некотором промежутке
имеет первообразную на некотором промежутке  , тогда для всех
, тогда для всех  имеет место равенство
имеет место равенство
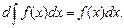
Отметим, что в этом равенстве под интегралом  понимается произвольная первообразная
понимается произвольная первообразная 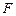 функции
функции 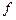 . Поэтому это равенство можно записать в виде
. Поэтому это равенство можно записать в виде

Справедливость последнего следует из того, что 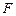 − первообразная
− первообразная 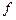 .
.
3) Если функция 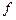 имеет первообразную на промежутке
имеет первообразную на промежутке  и
и 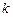 − число, то функция
− число, то функция  также имеет на
также имеет на  первообразную, причем при
первообразную, причем при  справедливо равенство
справедливо равенство 
4) Неопределенный интеграл от суммы двух функций равен сумме интегралов от этих функций, т.е. 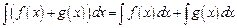 .
.
Лекция 8. Таблица интегралов. Основные способы интегрирования.
Приведем таблицу основных интегралов. Формулы таблицы являются следствием таблицы производных и определения неопределенного интеграла.
1.  ,
,  .
.
2.  .
.
3.  ,
,  .
.
4.  .
.
5.  .
.
6.  .
.
7. 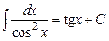 .
.
8.  .
.
9. 
10. 
11. 
12. 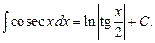
13.  .
.
14.  ,
,  .
.
15.  ,
,  .
.
16.  ,
,  .
.
Популярное:
- I. Понятие как форма мышления
- Microsoft Office Word. Дополнительные функции
- Абсорбционные ткани. Формирование, строение и выполняемые функции.
- Административно-правовые нормы: понятие, структура, виды. Дискуссионность по понятию структуры правовой нормы.
- АДМИНИСТРАТИВНО-ЮРИСДИКЦИОННОЕ ПРОИЗВОДСТВО: ПОНЯТИЕ, ЧЕРТЫ, ВИДЫ.
- Административные запреты и ограничения в структуре правового статуса государственных гражданских служащих в Российской Федерации: понятие и содержательная характеристика.
- АДМИНИСТРАТИВНЫЙ НАДЗОР: ПОНЯТИЕ, ОСОБЕННОСТИ, МЕТОДЫ, СУБЪЕКТЫ, ПОЛНОМОЧИЯ.
- Акты применения права:понятие,признаки,виды.Н,П,А.и акты примен.права:сходство,различия.
- Аминоспирты 2-аминоэтанол(коламин), холин, ацетилхолин. Аминофенолы: дофамин, норадреналин,адренлин.Аминотиолы ( 2 аминоэтантиол). Понятие о биологич-ой роли
- Амнистия и помилования. Понятие. Их правовое значение. (Статьи 84 —85).
- Анализ базовых функций гражданского общества. Демократические функции гражданского общества.
- Анатомо-морфологические особенности и основные физиологические функции организма

