Частные производные высших порядков. Если функция f(x, y) определена в некоторой области D, то ее частные производные и тоже
Если функция f(x, y) определена в некоторой области D, то ее частные производные  и
и 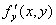 тоже будут определены в той же области или ее части.
тоже будут определены в той же области или ее части.
Будем называть эти производные частными производными первого порядка.
Производные этих функций будут частными производными второго порядка.


Продолжая дифференцировать полученные равенства, получим частные производные более высоких порядков.
Определение. Частные производные вида 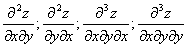
 и т.д. называются смешанными производными.
и т.д. называются смешанными производными.
38. Производные неявно заданной функции
Пусть дана дифференцируемая функция 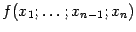 , для которой в некоторой точке
, для которой в некоторой точке 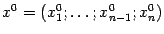 выполнено неравенство
выполнено неравенство 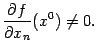 Тогда в некоторой окрестности точки
Тогда в некоторой окрестности точки 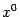 уравнение
уравнение 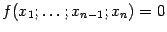 определяет, как мы знаем из теоремы о неявной функции, некоторую функцию
определяет, как мы знаем из теоремы о неявной функции, некоторую функцию  , заданную вблизи точки
, заданную вблизи точки 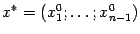 в
в 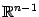 . Пусть требуется найти её частные производные
. Пусть требуется найти её частные производные  ,
,  . Это можно сделать, применив формулу производной сложной функции к функции
. Это можно сделать, применив формулу производной сложной функции к функции  которая тождественно равна 0 в окрестности точки
которая тождественно равна 0 в окрестности точки 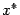 ; следовательно, и все её частные производные в точке
; следовательно, и все её частные производные в точке 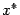 обращаются в 0. Итак, считая параметром, от которого зависят все аргументы функции
обращаются в 0. Итак, считая параметром, от которого зависят все аргументы функции 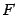 , переменную
, переменную 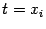 , где
, где 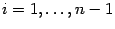 , получаем по формуле
, получаем по формуле 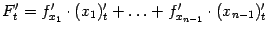 :
: 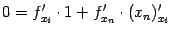 (производные
(производные 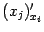 равны 0 при
равны 0 при 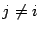 ,
, 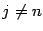 ), то есть
), то есть 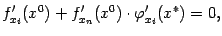 откуда
откуда 
 Эта важная формула позволяет вычислять производные неявно заданной функции
Эта важная формула позволяет вычислять производные неявно заданной функции 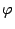 , не имея задающего её явного выражения. Пример Пусть функция
, не имея задающего её явного выражения. Пример Пусть функция 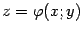 задана неявно уравнением
задана неявно уравнением  в окрестности точки
в окрестности точки 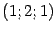 (проверьте, что координаты этой точки удовлетворяют уравнению). Найдём производные
(проверьте, что координаты этой точки удовлетворяют уравнению). Найдём производные 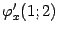 и
и  . Поскольку для функции
. Поскольку для функции 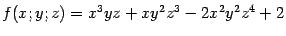 частные производные равны
частные производные равны 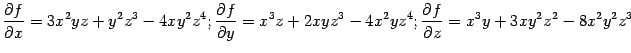 (и
(и  так что данное уравнение действительно определяет неявную функцию), то по формуле ( 7.9 ) получаем:
так что данное уравнение действительно определяет неявную функцию), то по формуле ( 7.9 ) получаем:  Подставляя координаты точки (1; 2; 1), находим:
Подставляя координаты точки (1; 2; 1), находим: 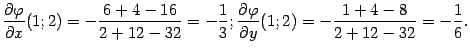
Вопрос 39.
Касательная плоскость и нормаль к поверхности
Пусть имеется поверхность, заданная уравнением  . Плоскость, в которой расположены все касательные прямые к линиям на поверхности, проходящим через данную точку
. Плоскость, в которой расположены все касательные прямые к линиям на поверхности, проходящим через данную точку 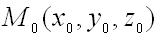 , называется касательной плоскостью к поверхности в точке
, называется касательной плоскостью к поверхности в точке  .
.
Прямая, проведенная через точку 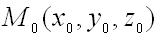 поверхности
поверхности  , перпендикулярно к касательной плоскости называется нормалью к поверхности.
, перпендикулярно к касательной плоскости называется нормалью к поверхности.
Если поверхность задана уравнением  , то уравнение касательной плоскости к этой поверхности в точке
, то уравнение касательной плоскости к этой поверхности в точке 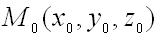 записывается в виде:
записывается в виде:
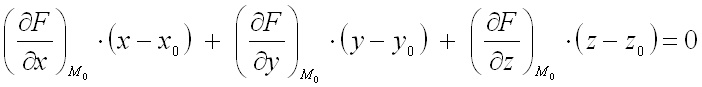 ,
,
а уравнение нормали к поверхности в этой же точке – в виде:
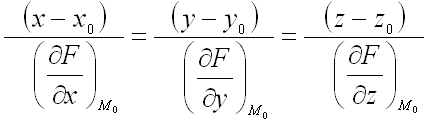 .
.
Примеры решения задач
Пример 1. Найти уравнение касательной плоскости и нормали к поверхности 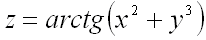 в точке
в точке  .
.
Решение.
Уравнение касательной плоскости к поверхности, заданной уравнением  , в точке
, в точке 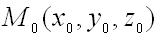 записывается в виде:
записывается в виде: 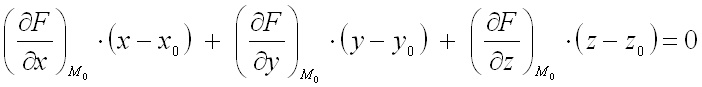 .
.
Так как в условии задачи уравнение поверхности задано в явном виде, то сначала его необходимо преобразовать к виду  :
: 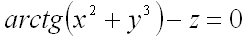 .
.
Теперь найдем частные производные  (при этом, в первых двух случаях используем правило дифференцирования сложной функции одной переменной):
(при этом, в первых двух случаях используем правило дифференцирования сложной функции одной переменной):
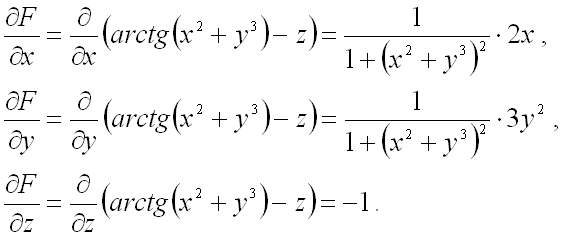
Вычислим значения частных производных первого порядка в точке  :
:
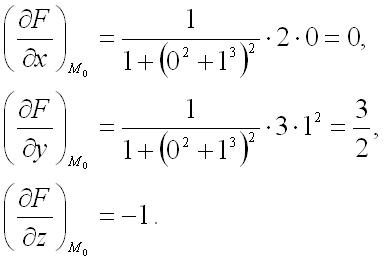
Подставим полученные значения в уравнение касательной плоскости:

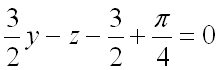 .
.
Вопрос 40.
Пусть в каждой точке некоторой области 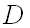 задана функция
задана функция 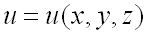 .
.
Вектор, проекциями которого на оси координат являются значения частных производных этой функции в соответствующей точке, называется градиентом функции 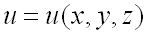 и обозначается
и обозначается  или
или 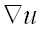 (читается «набла у»):
(читается «набла у»): 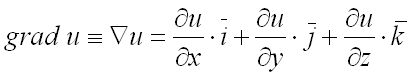 .
.
При этом говорят, что в области 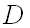 определено векторное поле градиентов.
определено векторное поле градиентов.
Для нахождения градиента функции 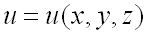 в заданной точке
в заданной точке 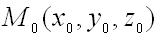 используют формулу:
используют формулу:
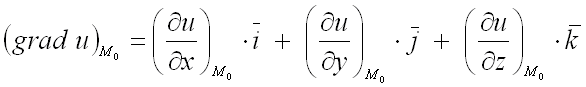 .
.
Свойства градиента
1. Производная в данной точке по направлению вектора 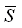 имеет наибольшее значение, если направление вектора
имеет наибольшее значение, если направление вектора 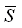 совпадает с направлением градиента. Это наибольшее значение производной равно
совпадает с направлением градиента. Это наибольшее значение производной равно 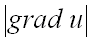 .
.
2. Производная по направлению вектора, перпендикулярного к вектору  , равна нулю.
, равна нулю.
Примеры решения задач
Пример 1. Найти производную от функции 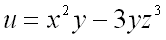 в точке
в точке  по направлению вектора
по направлению вектора  .
.
Решение.
Для решения задачи воспользуемся формулой для нахождения производной от функции 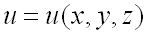 в заданной точке
в заданной точке 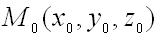 по направлению вектора
по направлению вектора  :
:
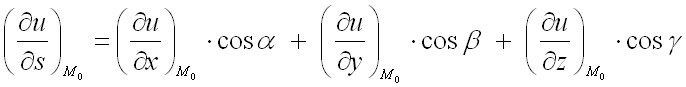 ,
,
где  – направляющие косинусы вектора
– направляющие косинусы вектора  , которые вычисляются по формулам:
, которые вычисляются по формулам:
 .
.
По условию задачи вектор  имеет координаты
имеет координаты  . Тогда его длина равна:
. Тогда его длина равна:
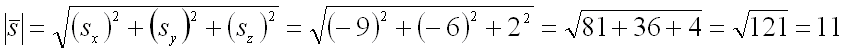 .
.
Следовательно, для направляющих косинусов вектора получим следующие значения:
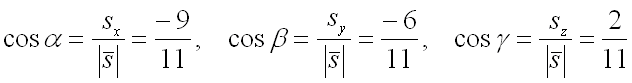 .
.
Далее для решения задачи необходимо найти все частные производные первого порядка от функции 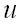 :
:

Вычислим значения этих частных производных первого порядка в точке  :
:
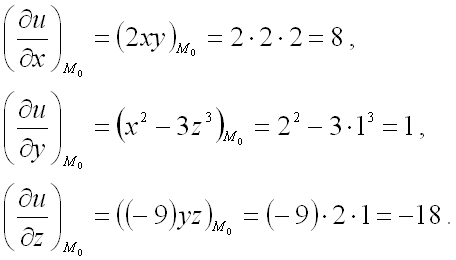
В заключении подставим полученные значения для направляющих косинусов вектора  и значения частных производных первого порядка от функции
и значения частных производных первого порядка от функции 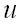 в точке
в точке  в формулу для нахождения производной по направлению в заданной точке:
в формулу для нахождения производной по направлению в заданной точке:
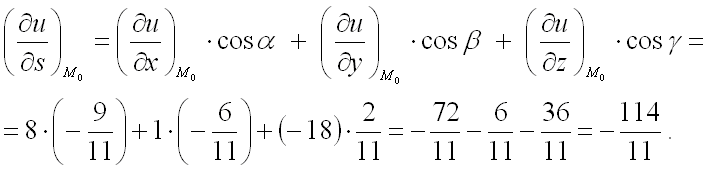
Ответ: производная от функции 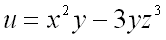 в точке
в точке  по направлению вектора
по направлению вектора  равна
равна 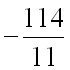 .
.
Вопрос 41.
Пусть в некоторой области 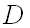 задана функция
задана функция 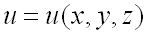 и точка
и точка  . Проведем из точки
. Проведем из точки 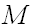 вектор
вектор 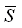 , направляющие косинусы которого
, направляющие косинусы которого  . На векторе
. На векторе 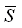 , на расстоянии
, на расстоянии 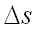 от его начала рассмотрим точку
от его начала рассмотрим точку  , т.е.
, т.е. 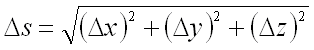 .
.
Будем предполагать, что функция 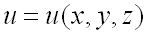 и ее частные производные первого порядка непрерывны в области
и ее частные производные первого порядка непрерывны в области 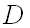 .
.
Предел отношения  при
при 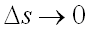 называется производной от функции
называется производной от функции 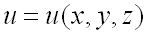 в точке
в точке  по направлению вектора
по направлению вектора 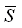 и обозначается
и обозначается 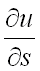 , т.е.
, т.е. 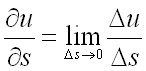 .
.
Для нахождения производной от функции 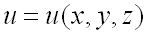 в заданной точке
в заданной точке 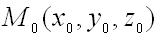 по направлению вектора
по направлению вектора  используют формулу:
используют формулу: 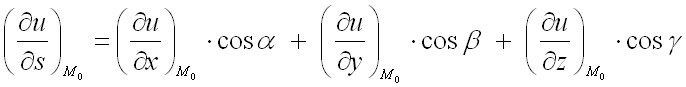 ,
,
где  – направляющие косинусы вектора
– направляющие косинусы вектора  , которые вычисляются по формулам:
, которые вычисляются по формулам:
 .
.
Вопрос 42.
Линии и поверхности уровня.
Для функции двух переменных, заданной уравнением (1.1), можно рассмотреть множество точек (х, у) плоскости Оху, для которых z принимает одно и то же постоянное значение, то есть z = const. Эти точки образуют на плоскости линию, называемую линией уровня.
Пример.
Найдем линии уровня для поверхности z = 4 — x² - y². Их уравнения имеют вид x² + y² = 4 — c (c=const) — уравнения концентрических окружностей с центром в начале координат и с радиусами. Например, при с=0 получаем окружностьx² + y² = 4.
Для функции трех переменных u = u (x, y, z) уравнение u (x, y, z) = c определяет поверхность в трехмерном пространстве, которую называют поверхностью уровня.
Пример.
Для функции u = 3x + 5y — 7z —12 поверхностями уровня будет семейство параллельных плоскостей, задаваемых уравнениями 3x + 5y — 7z —12 + с = 0.

