
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Уравнение поверхности и линии в пространстве ⇐ ПредыдущаяСтр 7 из 7
1) Основные понятия Поверхность в пространстве, как правило можно рассматривать как геометрическое место точек удовлетворяющих какому-либо условию. Например, сфера радиуса R с центром в т.О1.есть геометрическое место точек удаленных от т. О1 на расстояние R. Прямоугольная система координат Oxyz позволяет однозначно установить соответствие между точками пространства и тройками чисел x, y, z- их координатами. Свойства, общие всем точкам, можно записать в виде уравнения, связывающего координаты всех точек поверхности. Уравнение данной поверхности в прямоугольной системе координат Oxyz называют уравнением вида F(x, y, z)=0, с тремя переменными x, y, z которому удовлетворяют координаты каждой точки лежащей на поверхности и не удовлетворяют координаты точек не лежащие на поверхности. 2) Уравнение линии в пространстве Линию в пространстве можно рассматривать как линию пересечения двух поверхностей или как геометрическое место точек общих двум поверхностям. Если F1(x, y, z)=0 и F2(x, y, z) уравнения двух поверхностей, то координаты линии их пересечения (L) должно удовлетворять системе двух уравнений с тремя неизвестными
Линию в пространстве можно рассматривать и как траекторию движения точки. В этом случае ее задают векторным уравнением r=r(t) или параметрическим уравнениями.
3) Уравнение прямой в пространстве 1. Векторное уравнение прямой Положение прямой в пространстве вполне определено, если задать какую-либо точку M0 на прямой и вектор

      векторы точек M0 и M соответственно через векторы точек M0 и M соответственно через  и и  . Очевидно, что . Очевидно, что  = =  + + 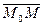 . Вектор . Вектор  М, лежащий на прямой L параллелен направляющему вектору М, лежащий на прямой L параллелен направляющему вектору  , поэтому , поэтому  M=t M=t  , где t- скалярный множитель, называемый параметром, может принимать различные значения в зависимости от положения точки M на прямой (рис.1.). Тогда уравнение можно записать в виде , где t- скалярный множитель, называемый параметром, может принимать различные значения в зависимости от положения точки M на прямой (рис.1.). Тогда уравнение можно записать в виде  = =  +t +t  - векторное уравнение прямой. - векторное уравнение прямой.
2. Параметрическое уравнение прямой Поскольку
исключая из параметрического уравнения прямой t получим:
4. Уравнение прямой проходящей через две точки Пусть прямая L проходит через точки M1(x1, y1, z1) и M2(x2, y2, z2). В качестве направляющего вектора
5. Угол между прямыми Пусть L1 и L2 заданы уравнениями
Если L1 перпендикулярна L2, то в этом случае cosφ =0, следовательно
Если L1 || L2, то векторы
4) Уравнение плоскости в пространстве.
Простейшей поверхностью является плоскость. Плоскость в пространстве Oxyz можно задать различными способами и каждому из них соответствует конкретное уравнение. 1. Уравнение плоскости проходящей через точку перпендикулярно вектору. Пусть в пространстве Oxyz плоскость Q задана точкой M0(x0, y0, z0) и вектором
-это уравнение плоскости проходящей через данную точку перпендикулярную вектору 2. Общее уравнение плоскости Рассмотрим общее уравнение первой степени с тремя переменными x, y и z.
Полагая, что по крайней мере, один из коэффициентов A, B или C≠ 0, например B≠ 0, перепишем его в виде:
Сравнивая полученное уравнение с ранее полученным (1) видим, что последнее является уравнением плоскости с нормальным вектором Частные случаи: а) Если D=0, то б) Если C=0, имеем в) Если C=D=0, то плоскость проходит через т.O(0, 0, 0) и || Oz, то есть проходит через ось Oz; г) Если A=B=0, то Cz+D=0, то есть Z= д) Если A=B=D=0, то Cz=0, то есть Z=0, это уравнение плоскости Oxy. 3. Уравнение плоскости, проходящей через три точки. Три точки в пространстве не лежащие на одной прямой определяют единственную плоскость. Найдем уравнение плоскости Q, проходящей через три данных точки M1(x1, y1, z1), M2(x2, y2, z2) и M3(x3, y3, z3), не лежащие на одной прямой. Возьмем на плоскости произвольную точку M(x, y, z) и составим векторы
-это уравнение есть уравнение плоскости, проходящей через три точки. 4. Уравнение плоскости в отрезках Пусть плоскость отсекает на осях Ox, Oy и Oz соответственно отрезки
5. Нормальное уравнение плоскости Положение плоскости Q можно определить заданием единичного вектора
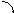            Пусть OK=P, а α, β и γ -углы, образованные вектором Пусть OK=P, а α, β и γ -углы, образованные вектором 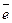 с осями Ox, Oy и Oz. Тогда с осями Ox, Oy и Oz. Тогда  = =  . Возьмем на плоскости произвольную точку M(x, y, z) и соединим ее с началом координат. Образуем вектор . Возьмем на плоскости произвольную точку M(x, y, z) и соединим ее с началом координат. Образуем вектор
точки M на плоскости Q проекция вектора
6. Угол между двумя плоскостями пусть заданы две плоскости Q1 и Q2:
Под углом между плоскостями понимают один из двугранных углов образованных этими плоскостями. Угол φ между нормальными векторами полученное равенство есть условие перпендикулярности Q1 и Q2. Если Q1 || Q2, то 7. Расстояние от точки до плоскости.
 (Pис.3) Найдем d- расстояние от точки до плоскости. Расстояние d от точки M0 до плоскости Q равно модулю проекции вектора M1M0 (Рис.3), где M1(x1, y1, z1)- произвольная точка плоскости Q на направление нормального вектора (Pис.3) Найдем d- расстояние от точки до плоскости. Расстояние d от точки M0 до плоскости Q равно модулю проекции вектора M1M0 (Рис.3), где M1(x1, y1, z1)- произвольная точка плоскости Q на направление нормального вектора  =(A, B, C). Следовательно =(A, B, C). Следовательно   = =
     = = 
    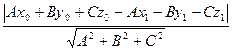
Так как т.M1 принадлежит Q, то
   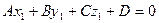 , и , и  , тогда уравнение примет вид: , тогда уравнение примет вид:
 . .
8.Угол между прямой и плоскостью Пусть плоскость задана уравнением
 
  
    Углом между прямой и плоскостью называется любой из двух смежных углов, образованных прямой и ее проекцией на плоскость. Углом между прямой и плоскостью называется любой из двух смежных углов, образованных прямой и ее проекцией на плоскость.
Пусть φ - угол между Q и L, а
Если L || Q, то Если L 9. Пересечение прямой с плоскостью Найти точку пересечения прямой
Для этого надо решить систему этих уравнений. Проще всего это сделать если записать уравнение прямой в параметрической форме:
Подставляя эти значения в уравнение плоскости получим Поверхности второго порядка 1) Цилиндрические поверхности. Поверхность, образованная движением прямой L, которая перемещается в пространстве, сохраняя постоянное направление, и пересекает каждый раз некоторую кривую K, называется цилиндрической поверхностью или цилиндром. При этом кривая K- называется направляющей, а L – образующей цилиндра. Будем рассматривать цилиндрические поверхности, направляющие которых лежат в одной из координатных плоскостей, а бразующие || координатной оси, то есть перпендикулярно этой плоскости. Пусть в Oxy лежит линия K, а ее уравнение F(x, y)=0. Построим цилиндр с образующими || оси Oz и направляющей K.
         Возьмем на цилиндре любую точку M(x, y, z). Она лежит на какой-то образующей. Пусть т.N- точка пересечения этой образующей с плоскостью Oxy. Следовательно, точка N лежит на кривой K, и ее координаты удовлетворяют уравнению линии K. Но точка M имеет такие же абсциссу x и ординату y, что и точка N. Возьмем на цилиндре любую точку M(x, y, z). Она лежит на какой-то образующей. Пусть т.N- точка пересечения этой образующей с плоскостью Oxy. Следовательно, точка N лежит на кривой K, и ее координаты удовлетворяют уравнению линии K. Но точка M имеет такие же абсциссу x и ординату y, что и точка N.
Следовательно, этому уравнению удовлетворяют и координаты точки M(x, y, z), так как оно не содержит Z. Так как M- любая точка цилиндра то уравнение F(x, y)=0, и будут уравнения цилиндра с образующими || оси Oz. В случае если образующая || оси Oy F(x, z)=0, если образующая || оси Ox; F(y, z)=0. Название цилиндра определяется формой направляющей. Если направляющей служит эллипс, в плоскости Oxy, то цилиндрическая поверхность называется эллиптическим цилиндром частный случай эллипса- окружность дает круговой цилиндр и т.д. все эти поверхности называются цилиндрами второго порядка, т.к. их уравнения есть уравнения второй степени. 2) Поверхности вращения. Конические поверхности. Поверхность, образованная вращением некоторой плоской кривой вокруг оси, лежащей в ее плоскости называется поверхностью вращения. Пусть некоторая кривая L лежит в плоскости Oyz. Уравнения этой кривой запишут в виде:
       Найдем уравнение поверхности образованное вращением кривой L вокруг оси Oz. Для этого возьмем на поверхности произвольную т.M(x, y, z). Проведем через M плоскость перпендикулярную оси Oz. Обозначим точки пересечения ее с осью Oz и кривой L соответственно O1 и N. Тогда O1(0, 0, z), а N(0, Найдем уравнение поверхности образованное вращением кривой L вокруг оси Oz. Для этого возьмем на поверхности произвольную т.M(x, y, z). Проведем через M плоскость перпендикулярную оси Oz. Обозначим точки пересечения ее с осью Oz и кривой L соответственно O1 и N. Тогда O1(0, 0, z), а N(0,  , z1). Отрезки O1M и O1N являются радиусами одной и той же окружности. Поэтому O1M=O1N, но , z1). Отрезки O1M и O1N являются радиусами одной и той же окружности. Поэтому O1M=O1N, но
Так как точка N лежит на кривой L, то ее координаты удовлетворяют уравнениям (1). Стало быть, F(y1, z1)=0, исключая вспомогательные координаты y1 и z1 придем к соотношению
Это уравнение - поверхности вращения, ему удовлетворяют координаты любой точки M этой поверхности и не удовлетворяют координаты точек не лежащих на поверхности вращения. Если кривая вращается вокруг других осей Ox и Oy, то уравнение будет носить аналогичный характер соответственно Поверхность, образованная прямыми линиями, проходящими через данную точку p и пересекающими данную плоскую линию L( не проходящую через p) называются конической поверхностью или конусом. При этом L- направляющая конуса p- ее вершина, а прямая описывающая поверхность называется образующей. Пусть направляющая L задана уравнениями:

 

       Возьмем на поверхности конуса произвольную точку M(z, y, z)(рис.3). Образующая, проходящая через точки P и M, пересекает направляющую L в некоторой точке N(x1, y1, z1) координаты точки N удовлетворяют выше записанным соотношениям, следовательно: Возьмем на поверхности конуса произвольную точку M(z, y, z)(рис.3). Образующая, проходящая через точки P и M, пересекает направляющую L в некоторой точке N(x1, y1, z1) координаты точки N удовлетворяют выше записанным соотношениям, следовательно: 
А канонические уравнения образующих проходящих через т.P и т. N имеют вид.
Исключая из этих уравнений Пример: составить уравнение конуса с вершиной в т.О(0, 0, 0).Если направляющая - эллипс Решение: Каноническое уравнение образующих, проходящих через т.О(0, 0, 0) и т.N(x1, y1, z1), полученную при пересечении образующей OM с эллипсом, будет 3) Канонические уравнения поверхностей второго порядка. По заданному уравнению поверхности второго порядка(те поверхности, уравнение которой в прямоугольной системе координат является алгебраическим уравнением второго порядка) будем определять ее геометрическим вид. Для этого применим так называемый метод сечений: исследование вида поверхности будем производить при помощи изучения линий пересечения данной поверхности с координатными плоскостями или плоскостями им параллельными. а) Эллипсоид Исследуем поверхность, заданную уравнением:
Рассмотрим сечения поверхности описываемой этим уравнением с плоскостями || плоскости Oxy. Уравнения этих плоскостей Z=h, где h- любое число. Линия, получаемая в сечении, будет определяться двумя уравнениями:
Исследуем это уравнение. а) Если |h|> c, c> 0, то б) Если |h|< c, то уравнения (1) можно записать в виде: т.е. линия пересечения есть эллипс с полуосями:
При этом, чем меньше |h|, тем больше полуоси
 
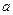 , b, c- называются полуосями , b, c- называются полуосями
эллипсоида, если б) Однополостный гиперболоид. Исследуем поверхность, заданную уравнением:
Пересекая эту поверхность плоскостью Z=h, получим линию пересечения, уравнение которой имеет вид:
Как видно, этой линий является эллипс с полуосями:
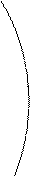  Полуоси Полуоси 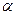 1 и b1 достигают min при h=0, 1 и b1 достигают min при h=0, 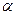 1= 1= 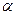 и b1=b. При возрастании |h| и b1=b. При возрастании |h| 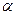 1 и b1 будут возрастать. 1 и b1 будут возрастать.

    Если пересекать эту поверхность плоскостями x=h и y=h, то в сечении получим гиперболы. Найдем, например, линию пересечения нашей поверхности с полуосью Oyz, уравнение которой x=0. Подставляя, получим: Если пересекать эту поверхность плоскостями x=h и y=h, то в сечении получим гиперболы. Найдем, например, линию пересечения нашей поверхности с полуосью Oyz, уравнение которой x=0. Подставляя, получим:
  -это гипербола -это гипербола
Анализ сечений показывает, что поверхность, определяемая нашим уравнением, имеют форму бесконечно расширяемой трубки. Эта поверхность называется однополостным гиперболоидом (рис.5.). с) Двухполосной гиперболоид Пусть поверхность задана уравнением:
Если эту поверхность пересечь плоскостью Z=h, получим линию пересечения, описываемую уравнениями: Отсюда следует, что: а) если |h|< c, то Z=h не пересекает поверхность; б) если |h|=с, то плоскости Z=c касаются данной поверхности в точках (0, 0, c) и (0, 0, -c); в) если |h|> c, то уравнения можно записать так:
 Пересекая поверхность координатными плоскостями Oyz(x=0) и Oxz(y=0), получим в сечении гиперболы, уравнения которых соответственно: Пересекая поверхность координатными плоскостями Oyz(x=0) и Oxz(y=0), получим в сечении гиперболы, уравнения которых соответственно: 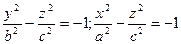
  
     У обеих гипербол действительной осью является ось Oz. Метод сечений позволяет изобразить эту поверхность, как поверхность, состоящую из двух полостей, имеющих форму выпуклых неограниченных чаш. Эта поверхность называется двуполостным гиперболоидом (рис.6.). У обеих гипербол действительной осью является ось Oz. Метод сечений позволяет изобразить эту поверхность, как поверхность, состоящую из двух полостей, имеющих форму выпуклых неограниченных чаш. Эта поверхность называется двуполостным гиперболоидом (рис.6.).
д) Эллиптический параболоид |
Последнее изменение этой страницы: 2017-03-14; Просмотров: 522; Нарушение авторского права страницы