Работа газа при изменении его объема

Для рассмотрения конкретных процессов найдем в общем виде внешнюю работу, совершаемую газом при изменении его объема. Рассмотрим, например, газ, находящийся под поршнем в цилиндрическом сосуде (рис. 56).

Если газ, расширяясь, передвигает поршень на бесконечно малое расстояние d , то производит над ним работу dА=Fd =pSd=pdV, где S - площадь поршня, Sd =dV - изменение объема системы. Таким образом,

dА = рdV.

Рис. 56

Полную работу А, совершаемую газом при изменении его объема от V₁
до V₂, найдем интегрированием формулы (2.4):

. (2.5)

Результат интегрирования определяется характером зависимости между давлением и объемом газа. Найденное для работы выражение (2.5) справедливо при любых изменениях объема твердых, жидких и газообразных тел.

Рис. 57

Произведенную при том или ином процессе работу можно изобразить графически с помощью кривой в координатах р, V. Например, изменение давления газа при его расширении изобразится кривой на рис. 57.

При увеличении объема на dV совершаемая газом работа равна pdV, т.е. определяется площадью полоски с основанием dV на рисунке. Поэтому полная работа, совершаемая газом при расширении от объема V₁ до объема V₂ определяется площадью, ограниченной осью абсцисс, кривой p=f(V) и прямыми V₁ и V₂.

Графически можно изображать только равновесные процессы, процессы состоящие из последовательности равновесных состояний. Они протекают так, что изменение термодинамических параметров за короткий промежуток времени бесконечно мало. Все реальные процессы неравновесны (они протекают с конечной скоростью), но в ряде случаев неравновесностью реальных процессов можно пренебречь (чем медленнее процесс протекает, тем он ближе к равновесному). В дальнейшем рассматриваемые процессы будем считать равновесными.

Теплоемкость

Удельная теплоемкость вещества - величина, равная количеству теплоты, необходимому для нагревания 1кг вещества на 1 К:

.

Единица удельной теплоемкости - джоуль на килограмм-кельвин.

Молярная теплоемкость - величина, равная количеству теплоты, необходимому для нагревания одного моля вещества на 1 К:

, (2.6)
где - количество вещества, выражающее число молей.

Единица молярной теплоемкости - джоуль на моль – кельвин .

 

 

Удельная теплоемкость с связана с молярной С_m соотношением

C_m=cM, (2.7)
где М - молярная масса вещества.

Различают теплоемкости при постоянном объеме и постоянном давлении, если в процессе нагревания вещества его объем или давление поддерживается постоянным.

Запишем выражение первого начала термодинамики (2.3) для 1 моля газа с учетом формул (2.4) и (2.6):

. (2.8)

Если газ нагревается при постоянном объеме, то работа внешних сил равна нулю (2.4) и сообщаемая газу извне теплота идет только на увеличение его внутренней энергии:

, (2.9)

т.е. молярная теплоемкость газа при постоянном объеме С_v равна изменению внутренней энергии 1 моля газа при повышении его температуры на 1 К. Согласно формуле (2.1),

,

тогда . (2.10)

Если газ нагревается при постоянном давлении, то выражение (2.8) можно записать в виде

.

Учитывая, что не зависит от вида процесса и всегда равна C_v (2.9);

продифференцировав уравнение Клапейрона–Менделеева pV_m=RT по Т (p=const), получим

. (2.11)
Выражение (2.11) называется уравнением Майера; оно показывает, что C_p всегда больше C_v на величину молярной газовой постоянной. Это объясняется тем, что при нагревании газа при постоянном давлении требуется еще дополнительное количество теплоты на совершение работы расширения газа, т.к. постоянство давления обеспечивается увеличением объема газа.

Использовав (2.10), выражение (2.11) можно записать в виде

. (2.11)
При рассмотрении термодинамических процессов важно знать характер-
ное для каждого газа отношение С_p к С_v

. (2.12)

Из формул (2.10) и (2.11) следует, что молярные теплоемкости определяются лишь числом степеней свободы и не зависят от температуры. Это утверждение молекулярно-кинетической теории справедливо в довольно широком интервале температур лишь для одноатомных газов. Уже у двухатомных газов число степеней свободы, проявляющихся в теплоемкости, зависит от температуры. Молекула двухатомного газа обладает тремя поступательными, двумя вращательными а с повышение температуры добавляются одна колебательная степень свободы.

По закону равномерного распределения энергии по степеням свободы, для комнатных температур.

Из качественной экспериментальной зависимости молярной теплоемкости С_v водорода (рис. 58) следует, что С_v зависит от температуры; при
низкой температуре (»50K), при комнатной - (вместо расчетных ) и очень высокой - .

Рис. 58

Это можно объяснить, предположив, что при низких температурах наблюдается только поступательное движение молекул, при комнатных - добавляетсяих вращение, а при высоких - к этим двум видам движения прибавляется еще и колебание молекул.

Расхождение теории и эксперимента нетрудно объяснить. Дело в том, что при вычислении теплоемкости надо учитывать квантование энергии вращения и колебаний молекул (возможны не любые вращательные и колебательные энергии, а лишь определенный дискретный ряд значений энергий). Если энергия теплового движения недостаточна, например, для возбуждения колебаний, то эти колебания не вносят своего вклада в теплоемкость (соответствующая степень свободы " замораживается" – к ней неприменим закон равнораспределения энергии). Этим объясняется, что теплоемкость моля двухатомного газа - водорода - при комнатной температуре равна вместо . Аналогично можно объяснить уменьшение теплоемкости при низкой температуре (" замораживаются вращательные степени свободы) и увеличение при высокой (" возбуждаются" колебательные степени свободы).

2.5. Применение первого начала термодинамики к изопроцессам

Среди равновесных процессов, происходящих с термодинамическими системами, выделяются изопроцессы, при которых один из основных параметров состояния сохраняется постоянным.

Изохорный процесс (V=const). Диаграмма этого процесса ( изохора ) в координатах р, V изображается прямой, параллельной оси ординат (рис. 59), где процесс 1-2 есть изохорное нагревание, а 1-3 - изохорное охлаждение. При изохорном процессе газ не совершает работы над внешними телами, т.е.

.

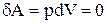Рис. 59

Для изохорного процесса следует, что вся теплота (рис.59), сообщаемая
газу, идет на увеличение его внутренней энергии:

dQ=dU

Согласно формуле (2.9),

DU_m=C_vdT.

⇐ Предыдущая567891011121314Следующая ⇒

Поделиться: