Момент инерции. Теорема Штейнера.

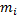Момент инерции определяется как , если распределение массы равномерно, то заменяется на – элементарный объём, – плотность вещества. .

Теорема Штейнера: момент инерции относительно произвольной оси равен сумме момента инерции относительно оси, параллельной данной и проходящей через центр инерции тела, и произведения массы тала на квадрат расстояния а между осями: .

Момент инерции:

1) однородного тонкого стержня массы , длины относительно оси, проходящей через центр масс и перпендикулярной стержню:

2) однородного тонкого стержня массы , длины относительно оси, проходящей через один из концов стержня:

3) тонкого кольца массы , радиуса R относительно оси симметрии, перпендикулярной плоскости кольца:

4) однородного диска (цилиндра) массы , радиуса R, высоты h относительно оси симметрии, перпендикулярной основанию: .

Кинетическая энергия вращающегося твёрдого тела.

При вращении тела с угловой скоростью все его элементарные массы движутся со скоростью они обладают кинетической энергией 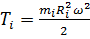, – для тела, вращающегося вокруг неподвижной оси. При вращении на материальные точки массы 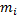, образующие твёрдое тело, действуют как внешние, так и внутренние силы. За промежуток времени 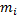испытывает перемещение 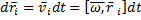, при этом силы совершают работу 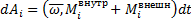. Работа всех сил будет равна . При сложении с учётом 3-его закона Ньютона сумма работ внутренних сил = 0. Следовательно, 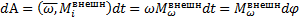. В соответствии с теоремой о кинетической энергии, приращение кинетической энергии = работе всех сил, действующих на тело .

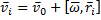Вычислим кинетическую энергию твёрдого тела, совершающего произвольное плоское движение. все точки движутся в параллельных плоскостях. Вращение совершается вокруг оси, перпендикулярно плоскостям, и движется вместе с некоторой точкой О. Скорость материальной точки массы представим в виде . Тело перемещается поступательно, следовательно, , – выражение кинетической энергии тела, совершающего произвольное плоское движение. Если в качестве точки О выбрать центр масс, тогда и .

Гироскопы.

Гироскоп (или волчок) – массивное твёрдое тело, симметричное некоторой оси, совершающее вращения вокруг неё с большой угловой скоростью. В силу симметрии гироскопа выполняется . При попытке повернуть вращающийся гироскоп вокруг некоторой оси наблюдается гироскопический эффект – под действием сил, которые, казалось бы, должны были вызвать поворот оси гироскопа ОО вокруг прямой О’O’, ось гироскопа поворачивается вокруг прямой О’’О’’ (ось ОО и прямая О’O’ предполагаются лежащими в плоскости чертежа, а прямая О’’О’’ и силы f1 и f2 – перпендикулярными к этой плоскости). Объяснение эффекта основано на использование уравнения момента . Момент импульса поворачивается вокруг оси ОХ в силу соотношения . Вместе с вокруг ОХ поворачивается и гироскоп. Вследствие гироскопического эффекта на подшипнике, на котором вращается гироскоп, начинают действовать гироскопические силы. Под действием гироскопических сил ось гироскопа стремиться занять положение, параллельное угловой скорости вращения Земли.

Описанное поведение гироскопа положено в основу гироскопического компаса. Преимущества гироскопа: указывает точное направление на географический северный полюс, его работа не подвержена воздействию металлических предметов.

Прецессия гироскопа – особый вид движения гироскопа имеет место в том случае, если момент действующих на гироскоп внешних сил, оставаясь постоянным по величине, поворачивается одновременно с осью гироскопа, образуя с ней всё время прямой угол. Рассмотрим движение гироскопа с одной закреплённой точкой на оси под действием силы тяжести , – расстояние от закреплённой точки до центра инерции гироскопа, – угол между гироскопом и вертикалью. направлен момент перпендикулярно к вертикальной плоскости, проходящей через ось гироскопа. 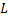Уравнение движения: приращение импульса = Следовательно, изменяет своё положение в пространстве таким образом, что его конец описывает окружность в горизонтальной плоскости. За промежуток времени гироскоп повернулся на угол ось гироскопа описывает конус вокруг вертикальной оси с угловой скоростью – угловая скорость прецессии.

Гармонические колебания.

Колебания – процессы, характеризующиеся той или иной степенью повторяемости по времени. В зависимости от физической природы повторяющегося процесса различают колебания: механические, электромагнитные, электромеханические и другие. Все эти процессы, несмотря на различную физическую природу, описываются одинаковыми математическими уравнениями и имеют ряд общих свойств. Рассмотрим небольшой шарик массы m, подвешенный на лёгкой упругой пружине жёсткости k. В положении равновесия (х=0) сумма сил, действующих на шар, равна 0, т.е. . При отклонении шарика от положения равновесия его движение будет описываться уравнением: . Уравнение запишем в следующем виде: . Положение тела описывается через функцию косинуса (или синуса), которая называется гармонической, поэтому такие колебания называются гармоническими. 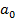– амплитуда колебаний – даёт максимальное отклонение от положения равновесия. – фаза колебания – определяется смещением тела в данный момент времени. – начальная фаза. Функция косинуса имеет период 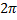. Значит, состояние колеблющегося тела повторяется при изменении фазы на 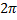. Промежуток времени, в течение которого фаза изменяется на 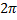, называется периодом колебаний . Период – время, за которое совершается одно полное колебание . Частота колебаний – количество колебаний за единицу времени , 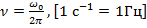. 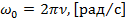– круговая (циклическая) частота, т.е. количество колебаний за 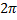секунд. Зная начальное положение и скорость тела, можно определить амплитуду и начальную фазу: .Движение тела при гармоническом колебании происходит под действием квазиупругой силы: , которая является консервативной, а, значит, выполняется закон сохранения энергии , . Среднее значение кинетической и потенциальной энергий по времени: .

⇐ Предыдущая123456Следующая ⇒

Поделиться: