Распространение волн в упругой среде. Уравнение плоской и сферической волны.
Если в каком-либо месте упругой среды (тв., жидк., газообр.) возникают колебания её частиц, то из-за взаимодействия между частицами эти колебания будут распространяться в среде от частицы к частице с некоторой скоростью v. Процесс распространения колебаний в пространстве называют волной. При этом частицы среды не совершают поступательного движения вместе с волной, а колеблются вблизи своего положения равновесия. В зависимости от направления колебаний частиц по отношению к направлению распространения волны различают продольные (частицы колеблются вдоль направления распространения волны) и поперечные (частицы колеблются перпендикулярно направлению распространения волны) волны. Продольные волны возникают в средах, где существуют упругие деформации сжатия или растяжения. Поперечные волны возникают при наличии упругой деформации сдвига. Геометрическое место точек, до которых доходят колебания к некоторому моменту времени, называют фронтом волны. Он перемещается в пространстве со временем. Геометрическое место точек, колеблющихся в одинаковой фазе, называют волновой поверхностью. 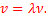 Длина волны – расстояние между 2-мя ближайшими точками, совершающими колебания с разностью фаз
Длина волны – расстояние между 2-мя ближайшими точками, совершающими колебания с разностью фаз 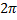 . В зависимости от формы волновой поверхности различают плоские, сферические и цилиндрические волны. Уравнением волны называется функция координат и времени, определяющая смещение точек среды из положения равновесия в любой момент времени во всём пространстве.
. В зависимости от формы волновой поверхности различают плоские, сферические и цилиндрические волны. Уравнением волны называется функция координат и времени, определяющая смещение точек среды из положения равновесия в любой момент времени во всём пространстве.
Уравнение плоской волны 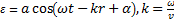 ,
, 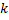 – волновое число.
– волновое число.
Уравнение сферической волны 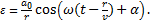
Волновое уравнение.
Уравнение любой волны есть решение некоторого дифференциального уравнения, называемого волновым. Исходя из физических свойств среды и основных законов механики мы получаем волновое уравнение из явного выражения для уравнения плоской волны.
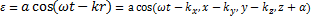 .
. 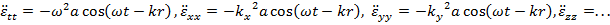 Можно записать:
Можно записать: 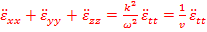 – волновое уравнение. Волновому уравнению будет удовлетворять любая волна произвольной частоты
– волновое уравнение. Волновому уравнению будет удовлетворять любая волна произвольной частоты 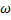 , распространяющаяся со скоростью
, распространяющаяся со скоростью 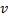 .
. 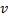 определяется физическими свойствами среды. В случае плоской волны, распространяющейся в направлении по х, волновое уравнение записывается в виде:
определяется физическими свойствами среды. В случае плоской волны, распространяющейся в направлении по х, волновое уравнение записывается в виде: 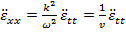 .
.
Скорость упругих волн в твёрдой среде.
Выясним, от каких физических свойств среды зависит скорость распространения волны. Рассмотрим плоскую волну, распространяющуюся в направлении ОХ в твёрдой упругой среде. Распространение колебаний происходит за счёт сил упругости в различных сечениях, перпендикулярных ОХ, поэтому будут различны и возникающие силы упругости, а также нормальное напряжение. Будем рассматривать продольные волны. Из-за неоднородности возникающих механических напряжений вместо закона Гука 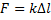 следует рассматривать законГука в дифференциальной форме
следует рассматривать законГука в дифференциальной форме 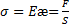 – механическое напряжение. В случае неоднородных растяжений или сжатий относительные деформации будут различны в различных сечениях. Выделим в среде цилиндрический объем с площадью основания
– механическое напряжение. В случае неоднородных растяжений или сжатий относительные деформации будут различны в различных сечениях. Выделим в среде цилиндрический объем с площадью основания 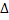 S и высотой
S и высотой 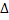 x. Если основание цилиндра с координатой х имеет в некоторый момент времени смещение, то смещение основания с координатой x, x+
x. Если основание цилиндра с координатой х имеет в некоторый момент времени смещение, то смещение основания с координатой x, x+ 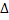 x будет x+
x будет x+ 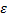 , x+
, x+ 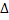 x+
x+ 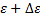 .
. 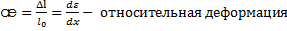 .
. 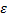 – абсолютная погрешность. Следовательно, закон Гука записывается
– абсолютная погрешность. Следовательно, закон Гука записывается 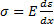 . Выберем цилиндр с достаточно малой высотой
. Выберем цилиндр с достаточно малой высотой 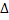 x, чтобы можно было считать ускорения всех его частиц одинаковыми. Тогда его движение будет подчиняться 2-ому закону Ньютона. Масса цилиндра
x, чтобы можно было считать ускорения всех его частиц одинаковыми. Тогда его движение будет подчиняться 2-ому закону Ньютона. Масса цилиндра 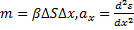 . Воспользуемся разложением функции
. Воспользуемся разложением функции 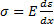 . в ряду Тейлора. Из-за малости +
. в ряду Тейлора. Из-за малости + 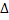 x+
x+ 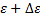 и
и 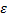 ограничимся разложением величин 1-ого порядка. Преобразуем и получим:
ограничимся разложением величин 1-ого порядка. Преобразуем и получим: 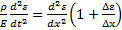 .
.
При упругих колебаниях относительная деформация мала, и (или) ей можно пренебречь 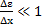 . Таким образом, получаем волновое уравнение
. Таким образом, получаем волновое уравнение 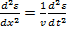 . Скорость распространения волны определяется модулем Юнга и плотностью среды:
. Скорость распространения волны определяется модулем Юнга и плотностью среды: 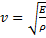
Энергия упругой волны.
Пусть плоская продольная волна распространяется в направлении ОХ в некоторой упругой среде. Её уравнение: 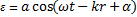 . Частицы среды, отклоняясь от положения равновесия, движутся с некоторыми скоростями. Следовательно, они обладают кинетической и потенциальной энергиями. Выделим в среде цилиндрический объем
. Частицы среды, отклоняясь от положения равновесия, движутся с некоторыми скоростями. Следовательно, они обладают кинетической и потенциальной энергиями. Выделим в среде цилиндрический объем 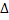 V с площадью основания
V с площадью основания 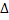 S и высотой
S и высотой 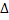 x. Его величина такова, что можем считать скорости частиц
x. Его величина такова, что можем считать скорости частиц 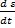 и относительное смещение
и относительное смещение 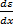 одинаковыми.
одинаковыми. 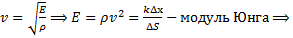 Энергия, заключённая в этом объёме
Энергия, заключённая в этом объёме 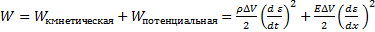 . Таким образом, плотность энергии упругой волны
. Таким образом, плотность энергии упругой волны 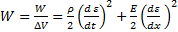 . Подставим в него уравнение плоской волны, преобразуем и воспользуемся тем, что
. Подставим в него уравнение плоской волны, преобразуем и воспользуемся тем, что 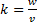 :
: 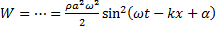 . Затем найдём среднюю по периоду плотность энергии:
. Затем найдём среднюю по периоду плотность энергии: 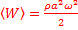 . Из выражения для плотности энергии видно, что её величина меняется со временем от 0 до некоторого максимального значения, а значит, энергия от источников колебания переносится волной из одного места пространства в другое со скоростью
. Из выражения для плотности энергии видно, что её величина меняется со временем от 0 до некоторого максимального значения, а значит, энергия от источников колебания переносится волной из одного места пространства в другое со скоростью 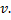 Волна осуществляет процесс переноса энергии, но не вещества. Перенос энергии осуществляется посредством сил упругого взаимодействия между частицами среды. Количество энергии, переносимое через некоторую поверхность за единицу времени, называется потоком энергии через эту поверхность:
Волна осуществляет процесс переноса энергии, но не вещества. Перенос энергии осуществляется посредством сил упругого взаимодействия между частицами среды. Количество энергии, переносимое через некоторую поверхность за единицу времени, называется потоком энергии через эту поверхность: 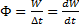 . Для более детальной характеристики процесса переноса энергии используется вектор плотности потока энергии
. Для более детальной характеристики процесса переноса энергии используется вектор плотности потока энергии 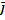 . По величине он равен потоку энергии, переносимой через площадку, перпендикулярную направлению распространения волны, делённому на площадь этой площадки:
. По величине он равен потоку энергии, переносимой через площадку, перпендикулярную направлению распространения волны, делённому на площадь этой площадки: 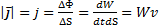 – последнее – вектор Умова. По направлению он совпадает с направлением распространения волны. Среднее
– последнее – вектор Умова. По направлению он совпадает с направлением распространения волны. Среднее 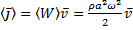 . Модуль этого выражения называется интенсивностью волны.
. Модуль этого выражения называется интенсивностью волны.

