| Формула для вычислений
| Функция или инструмент Анализа данных в Excel
| Результат вычислений /Примечания
|
Оценка параметров модели парной и множественной линейной регрессии
| Для вычисления параметров уравнения регрессии следует воспользоваться инструментом Регрессияиз пакетаАнализ данных
| Возвращает подробную информацию о параметрах модели, качестве модели, расчетных значениях и остатках в виде четырех таблиц: Регрессионная статистика, Дисперсионный анализ, Коэффициенты, Вывод остатка.
Также могут быть получены график подбора и график остатков
|
| Оценка качества модели регрессии
|
F-критерий Фишера для проверки значимости модели регрессии
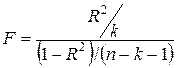
| =FРАСПОБР(вероятность; степени_
свободы1; степени_свободы2)
вероятность – это вероятность, связанная с F-распределением
степени_свободы 1 – это числитель степеней свободы (n1 = k)
степени_свободы 2 – это знаменатель степеней свободы (n2 = (n – k– 1),
где k – количество факторов, включенных в модель)
| Возвращает обратное значение для F-распределения вероятностей.
FРАСПОБР( ) можно использовать, чтобы определить критические значения F-распределения.
Чтобы определить критическое значение F, нужно использовать уровень значимости α как аргумент вероятность для FРАСПОБР( ).
|
Коэффициент детерминации
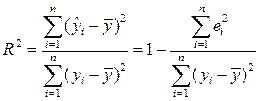
| Коэффициент детерминациипоказывает долю вариации результативного признака, находящегося под воздействием изучаемых факторов, то есть определяет, какая доля вариации признака Y учтена в модели и обусловлена влиянием на него факторов.
Чем ближе R2 к 1, тем выше качество модели
|
Коэффициент множественной корреляции (индекс корреляции) R
R =  =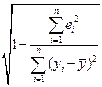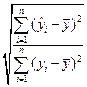 
| Данный коэффициент является универсальным, так как он отражает тесноту связи и точность модели, а также может использоваться при любой форме связи переменных.
Чем ближе R к 1, тем выше качество модели
|
t-критерий Стьюдента для оценки значимости параметров модели линейной регрессии:
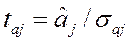
| Вычисленное значение  сравнивается с критическим значением t-критерия, которое берется из таблицы значений t-распределения Стьюдента с учетом заданного уровня значимости и числа степеней свободы (n – k – 1). В Excel критическое значение t-критерия можно получить с помощью функции
СТЬЮДРАСПОБР(вероятность; степени_свободы)
вероятность – вероятность, соответствующая двустороннему распределению Стьюдента
степени_свободы – число степеней свободы, характеризующее распределение
|
Средняя относительная ошибка аппроксимации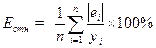 
| Средняя относительная ошибка аппроксимации – оценка точности модели
|
| Оценка влияния отдельных факторов на зависимую переменную на основе модели
|
Коэффициенты эластичности
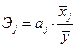
| Коэффициент эластичности показывает, на сколько процентов изменится значение исследуемой величины при изменении соответствующего фактора на 1%
|
Бета-коэффициенты
| Бета-коэффициент показывает, на какую часть своего СКО изменится значение исследуемой переменной при изменении соответствующего фактора на 1 СКО
|
Дельта-коэффициенты
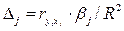
| Дельта-коэффициент показывает среднюю долю влияния соответствующего фактора в совокупном влиянии всех факторов, включенных в модель
|
| Построение интервальных прогнозов по модели регрессии
|
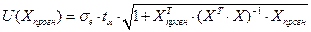 – ошибка прогнозирования, которая позволяет определить доверительный интервал прогноза,
где  – стандартная ошибка модели
|
| | | | | | |
