Выбор факторных признаков для построения регрессионной модели методом исключения
Для проведения регрессионного анализа используем инструмент Регрессия (надстройка Анализ данных в Excel).
На первом шаге строится модель регрессии по всем факторам:
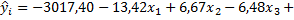 12, 24 12, 24 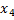 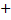 30, 48 30, 48 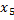 . .
(10, 38) (3, 01) (15, 78) (14, 41) (11, 52)
В скобках указаны значения стандартных ошибок коэффициентов регрессии.
Фрагмент протокола регрессионного анализа приведен в табл. 4.
Таблица 4. Модель регрессии по пяти факторам
| | Коэффициенты
| Стандартная ошибка
| t-статистика
| P-значение
| Нижние 95%
| Верхние 95%
| | Y – пересечение
| –3017, 40
| 1094, 49
| –2, 76
| 0, 02
| –5456, 06
| –578, 73
| | Время – Х1
| –13, 42
| 10, 38
| –1, 29
| 0, 23
| –36, 54
| 9, 71
| | Затраты на рекламу – Х2
| 6, 67
| 3, 01
| 2, 22
| 0, 05
| –0, 03
| 13, 38
| | Цена товара – Х3
| –6, 48
| 15, 78
| –0, 41
| 0, 69
| –41, 63
| 28, 68
| | Средняя цена товара у конкурентов – Х4
| 12, 24
| 14, 41
| 0, 85
| 0, 42
| –19, 87
| 44, 34
| | Индекс потребительских расходов – Х5
| 30, 48
| 11, 52
| 2, 64
| 0, 02
| 4, 80
| 56, 15
| | | | | | | | | |
В данном случае коэффициенты уравнения регрессии при Х1, Х3, Х4 незначимы при 5%-ном уровне значимости. После построения уравнения регрессии и оценки значимости всех коэффициентов регрессии из модели исключают тот фактор, коэффициент при котором незначим и имеет наименьший по абсолютной величине коэффициент t, а именно Х3.
После этого получают новое уравнение множественной регрессии 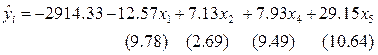
и снова производят оценку значимости всех оставшихся коэффициентов регрессии (табл. 5).
Таблица 5. Модель регрессии по четырем факторам
| | Коэффициенты
| Стандартная ошибка
| t-статистика
| P-значение
| Нижние 95%
| Верхние 95%
| | Y – пересечение
| –2914, 33
| 1024, 23
| –2, 85
| 0, 02
| –5168, 65
| –66, 00
| | Время – Х1
| –12, 57
| 9, 78
| –1, 29
| 0, 23
| –34, 09
| 8, 95
| | Затраты на рекламу – Х2
| 7, 13
| 2, 69
| 2, 65
| 0, 02
| 1, 20
| 13, 05
| | Средняя цена товара у конкурентов – Х4
| 7, 93
| 9, 49
| 0, 84
| 0, 42
| –12, 96
| 28, 82
| | Индекс потребительских расходов – Х5
| 29, 15
| 10, 64
| 2, 74
| 0, 02
| 5, 74
| 52, 56
|
Так как среди них есть незначимые (Х1 и Х4), то исключают фактор с наименьшим значением t-критерия – Х4. В табл. 6 представлены результаты, полученные после исключения фактора Х4. На следующем шаге исключаем незначимый фактор Х1.
Таблица 6. Модель регрессии по трем факторам
| | Коэффициенты
| Стандартная ошибка
| t-статистика
| P-значение
| Нижние 95%
| Верхние 95%
| | Y – пересечение
| –2957, 61
| 1009, 97
| –2, 93
| 0, 01
| –5158, 15
| –2957, 61
| | Время – Х1
| –14, 32
| 9, 43
| –1, 52
| 0, 15
| –34, 86
| –14, 32
| | Затраты на рекламу – Х2
| 7, 23
| 2, 65
| 2, 72
| 0, 02
| 1, 45
| 7, 23
| | Индекс потребительских расходов – Х5
| 30, 95
| 10, 28
| 3, 01
| 0, 01
| 8, 54
| 30, 95
|
Процесс исключения факторов останавливается на том шаге, при котором все регрессионные коэффициенты значимы (табл. 7).
Таблица 7. Модель регрессии со значимыми факторами
| | Коэффициенты
| Стандартная ошибка
| t-статистика
| P-значение
| Нижние 95%
| Верхние 95%
| | Y – пересечение
| –1471, 31
| 259, 77
| –5, 66
| 0, 00
| –2032, 50
| –910, 12
| | Затраты на рекламу – Х2
| 9, 57
| 2, 27
| 4, 22
| 0, 00
| 4, 67
| 14, 46
| | Индекс потребительских расходов – Х5
| 15, 75
| 2, 47
| 6, 39
| 0, 00
| 10, 42
| 21, 08
| | | | | | | | | |
Получено уравнение регрессии, все коэффициенты которого значимы не только при 5%-ном уровне значимости, но и при 1%-ном уровне значимости:
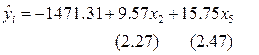 . .
Оценка параметров модели. Экономическая интерпретация коэффициентов регрессии
В результате применения различных подходов к выбору факторов пришли к выводу о необходимости включения в модель двух факторов – Затраты на рекламу и Индекс потребительских расходов.
Выполняя матричные вычисления по формуле  , естественно, получим такое же уравнение регрессии, как и при использовании инструмента Регрессия в Анализе данных (рис. 2). Уравнение зависимости объема реализации от затрат на рекламу и индекса потребительских расходов можно записать в следующем виде: , естественно, получим такое же уравнение регрессии, как и при использовании инструмента Регрессия в Анализе данных (рис. 2). Уравнение зависимости объема реализации от затрат на рекламу и индекса потребительских расходов можно записать в следующем виде:
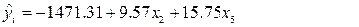
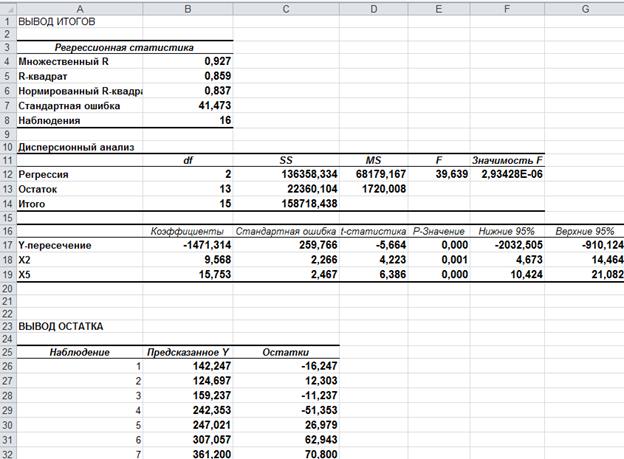
Рис. 2. Результаты работы с инструментом Регрессия
коэффициент регрессии aj показывает, на какую величину в среднем изменится результативный признак Y, если переменную xj увеличить на единицу измерения, то есть aj является нормативным коэффициентом.
В нашей задаче величина, равная 9, 57 (коэффициент при х2), показывает, что при увеличении затрат на рекламу на 1000 руб. объем реализации увеличится на 9, 57 тыс. руб., а если на 1% увеличится индекс потребительских расходов, то объем реализации увеличится на 15, 75 тыс. руб.
Расчетные значения Y определяются путем последовательной подстановки в эту модель значений факторов, взятых для каждого наблюдения, или из последней таблицы регрессионного анализа Вывод остатка (столбец Предсказанное Y ).
|

