
|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |

|
Архитектура Аудит Военная наука Иностранные языки Медицина Металлургия Метрология Образование Политология Производство Психология Стандартизация Технологии |
Первое достаточное условие существования точки перегиба ⇐ ПредыдущаяСтр 5 из 5
Если функция f(x) непрерывна и дифференцируема в точке x0, имеет вторую производную f′ ′ (x0) в некоторой проколотой δ -окрестности точки x0 и если вторая производная меняет знак при переходе через точку x0, то x0 является точкой перегиба функции f(x). при переходе через точку x0 меняет знак с плюса на минус. Следовательно , в левой δ -окрестности (x0− δ, x0) выполняется неравенство f′ ′ (x)> 0, а в правой δ -окрестности (x0, x0+δ ) справедливо неравенство f′ ′ (x)< 0. функция f(x) выпукла вниз в левой δ -окрестности точки x0 и выпукла вверх в правой δ -окрестности. выпуклости, т.е. c является, по определению, точкой перегиба. Второе достаточное условие существования Точки перегиба Пусть f′ ′ (x0)=0, f′ ′ ′ (x0)≠ 0. Тогда точка x0 является точкой перегиба функции f(x). в точке x0 либо строго возрастает (если f′ ′ ′ (x0)> 0), либо строго убывает (если f′ ′ ′ (x0)< 0). Так как f′ ′ (x0)=0, то вторая производная при некотором δ > 0 имеет разные знаки в левой и правой δ -окрестности точки x0. Отсюда, на основании предыдущей теоремы, следует что x0 − точка перегиба функции f(x). | ||
Вопрос. Понятие первообразной и неопределённого интеграла. Основные свойства неопределённого интеграла. Примеры.
Неопределенный интеграл. Понятие первообразной
Первообразная, основные понятия и определения
Определение
Функция 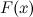 называется первообразной для функции
называется первообразной для функции 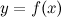 на промежутке
на промежутке 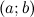 , конечном или бесконечном, если функция
, конечном или бесконечном, если функция 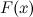 дифференцируема в каждой точке этого промежутка и ее производная удовлетворяет следующему равенству:
дифференцируема в каждой точке этого промежутка и ее производная удовлетворяет следующему равенству:
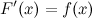
Последнее равенство можно записать через дифференциалы:
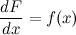 или
или 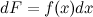
Функция 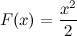 является первообразной для функции
является первообразной для функции 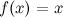 , так как
, так как
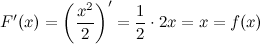
Первообразная 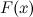 имеет конечную производную, а, следовательно, является непрерывной функцией.
имеет конечную производную, а, следовательно, является непрерывной функцией.
Теорема
(О бесконечном множестве первообразных для функции)
Если функция 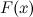 является первообразной для функции
является первообразной для функции 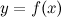 на некотором промежутке, то и функция
на некотором промежутке, то и функция 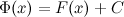 , где
, где 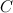 - произвольная постоянная, также будет первообразной для функции
- произвольная постоянная, также будет первообразной для функции 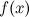 на рассматриваемом промежутке.
на рассматриваемом промежутке.
для функции 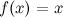 первообразной является функция
первообразной является функция 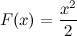 , а, следовательно, и все функции вида
, а, следовательно, и все функции вида 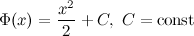 также будут первообразными, так как выполняется равенство
также будут первообразными, так как выполняется равенство 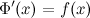 :
:
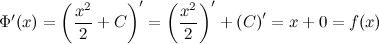
Таким образом, если функция 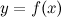 имеет первообразную, то она имеет бесконечное множество первообразных.
имеет первообразную, то она имеет бесконечное множество первообразных.
Теорема
(Об общем виде первообразной для функции)
Если функции 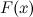 и
и 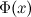 - две любые первообразные функции
- две любые первообразные функции 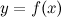 , то их разность равна некоторой постоянной, то есть
, то их разность равна некоторой постоянной, то есть
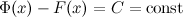
Последнюю теорему можно сформулировать иначе: каждая функция, которая является первообразной для функции 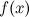 , может быть представлена в виде
, может быть представлена в виде 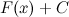 .
.
Неопределенный интеграл
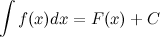
Знак 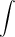 называется интегралом,
называется интегралом, 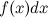 - подынтегральным выражением,
- подынтегральным выражением, 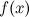 - подынтегральной функцией, а
- подынтегральной функцией, а  - переменной интегрирования.
- переменной интегрирования.
Операция нахождения первообразной или неопределенного интеграла от функции 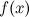 называется интегрированием функции
называется интегрированием функции 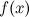 . Интегрирование представляет собой операцию, обратную дифференцированию.
. Интегрирование представляет собой операцию, обратную дифференцированию.
Геометрическая интерпретация неопределенного интеграла
Неопределенный интеграл представляет собой семейство параллельно расположенных кривых 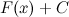 , где каждому конкретному числовому значению постоянной
, где каждому конкретному числовому значению постоянной 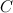 соответствует определенная кривая из указанного семейства.
соответствует определенная кривая из указанного семейства.

График каждой кривой из семейства называется интегральной кривой.
Теорема
Каждая непрерывная на промежутке 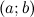 функция, имеет на этом интервале первообразную.
функция, имеет на этом интервале первообразную.
Свойства неопределенного интеграла
1. Дифференциал от неопределенного интеграла равен подынтегральному выражению
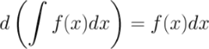
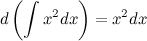
2. Производная от неопределенного интеграла равна подынтегральной функции
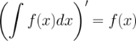
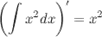
3. Неопределенный интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная
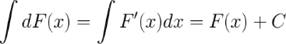
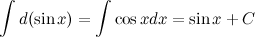
4. Постоянный множитель можно выносить за знак неопределенного интеграла или вносить под знак интеграла
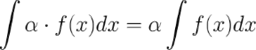
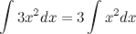
5. Неопределенный интеграл от суммы/разности двух и больше функций равен сумме/разности неопределенных интегралов от этих функций
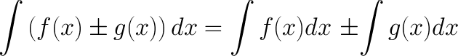

6. Если 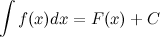 , то и
, то и  , где функция
, где функция  - произвольная функция с непрерывной производной.
- произвольная функция с непрерывной производной.
Известно, что 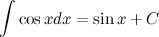 , а тогда
, а тогда 
Последнее изменение этой страницы: 2017-03-15; Просмотров: 361; Нарушение авторского права страницы