Распространение волн в упругой среде

Волны

 

Основными видами волн являются упругие (например, звуковые и сейсмические волны), волны на поверхности жидкости и электромагнитные волны (в том числе световые и радиоволны). Характерная особенность волн состоит в том, что при их распространении происходит перенос энергии без переноса вещества. Рассмотрим вначале распространение волн в упругой среде.

 

Распространение волн в упругой среде

Колеблющееся тело, помещённое в упругую среду, будет увлекать за собой, и приводить в колебательное движение прилегающие к нему частицы среды. Последние, в свою очередь, будут воздействовать на соседние частицы. Ясно, что увлекаемые частицы будут отставать по фазе от тех частиц, которые их увлекают, так как передача колебаний от точки к точке всегда осуществляется с конечной скоростью.

Итак, колеблющееся тело, помещённое в упругую среду, является источником колебаний, распространяющихся от него во все стороны.

Процесс распространения колебаний в среде называется волной. Или упругой волной называется процесс распространения возмущения в упругой среде.

Волны бывают поперечными (колебания происходят в плоскости перпендикулярной направлению распространения волны). К ним относятся электромагнитные волны. Волны бывают продольными, когда направление колебаний совпадает с направлением распространения волны. Например, распространение звука в воздухе. Сжатие и разряжение частиц среды происходят в направлении распространения волны.

Волны могут иметь различную форму, могут быть регулярными и нерегулярными. Особое значение в теории волн имеет гармоническая волна, т.е. бесконечная волна, в которой изменение состояния среды происходит по закону синуса или косинуса.

Рассмотрим упругие гармонические волны. Для описания волнового процесса используется ряд параметров. Запишем определения некоторых из них. Возмущение, происшедшее в некоторой точке среды в некоторый момент времени, распространяется в упругой среде с определенной скоростью. Распространяясь от источника колебаний, волновой процесс охватывает все новые и новые части пространства.

Геометрическое место точек, до которых доходят колебания к некоторому моменту времени , называется фронтом волны или волновым фронтом.

Фронт волны отделяет часть пространства, уже вовлеченную в волновой процесс, от области, в которой колебания еще не возникли.

Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой поверхностью.

Волновых поверхностей может быть множество, волновой фронт в каждый момент времени один.

Волновые поверхности могут быть любой формы. В простейших случаях они имеют форму плоскости или сферы. Соответственно волна в этом случае называется плоской или сферической. В плоской волне волновые поверхности представляют собой множество параллельных друг другу плоскостей, в сферической волне – множество концентрических сфер.

Пусть плоская гармоническая волна распространяется со скоростью вдоль оси . Графически такая волна изображается в виде функции (дзета) для фиксированного момента времени и представляет собой зависимость смещения точек с различными значениями от положения равновесия. – это расстояние от источника колебаний , на котором находится, например, частица . Рисунок дает мгновенную картину распределения возмущений вдоль направления распространения волны. Расстояние , на которое распространяется волна за время, равное периоду колебаний частиц среды, называется длиной волны.

,

где – скорость распространения волны.

 

Групповая скорость

Строго монохроматическая волна представляет собой бесконечную во времени и пространстве последовательность " горбов" и " впадин".

(1)

Фазовая скорость этой волны или (2)

С помощью такой волны нельзя передать сигнал, т.к. в любой точке волны все " горбы" одинаковы. Сигнал должен отличаться. Быть знаком (меткой) на волне. Но тогда волна уже не будет гармонической, и не будет описываться уравнением (1). Сигнал (импульс) можно представить согласно теореме Фурье в виде суперпозиции гармонических волн с частотами, заключёнными в некотором интервале Dw. Суперпозиция волн, мало отличающихся друг от друга по частоте,

называется волновым пакетом или группой волн.

Выражение для группы волн может быть записано следующим образом.

(3)

Значок w подчеркивает, что эти величины зависят от частоты.

Этот волновой пакет может быть суммой волн с мало отличающимися частотами. Там, где фазы волн совпадают, наблюдается усиление амплитуды, а там, где фазы противоположны, наблюдается гашение амплитуды (результат интерференции). Такая картина представлена на рисунке. Чтобы суперпозицию волн можно было считать группой волн необходимо выполнение следующего условия Dw < < w₀.

В недиспергирующей среде все плоские волны, образующие волновой пакет, распространяются с одинаковой фазовой скоростью v. Дисперсия это зависимость фазовой скорости синусоидальной волны в среде от частоты. Явление дисперсии мы рассмотрим позже в разделе " Волновая оптика". В отсутствии дисперсии скорость перемещения волнового пакета совпадает с фазовой скорость v. В диспергирующей среде каждая волна диспергирует со своей скоростью. Поэтому волновой пакет с течением времени расплывается, его ширина увеличивается.

Если дисперсия невелика, то расплывание волнового пакета происходит не слишком быстро. Поэтому движению всего пакета можно приписать некоторую скорость U.

Скорость, с которой перемещается центр волнового пакета (точка с максимальным значением амплитуды) называется групповой скоростью.

В диспергирующей среде v¹ U. Вместе с движением самого волнового пакета происходит движение " горбов" внутри самого пакета. " Горбы" перемещаются в пространстве со скоростью v, а пакет в целом со скоростью U.

Рассмотрим подробнее движение волнового пакета на примере суперпозиции двух волн с одинаковой амплитудой и разными частотами w (разными длинами волн l ).

Запишем уравнения двух волн. Примем для простоты начальные фазы j₀ = 0.

Здесь

Пусть Dw < < w, соответственно Dk < < k.

Сложим колебания и проведём преобразования с помощью тригонометрической формулой для суммы косинусов:

В первом косинусе пренебрежём Dwt и Dkx, которые много меньше других величин. Учтём, что cos(–a) = cosa. Окончательно запишем.

(4)

Множитель в квадратных скобках изменяется от времени и координаты значительно медленнее, чем второй множитель. Следовательно, выражение (4) можно рассматривать как уравнение плоской волны с амплитудой, описываемой первым сомножителем. Графически волна, описываемая выражением (4) представлена на рисунке, изображённом выше.

Результирующая амплитуда получается в результате сложения волн, следовательно, будут наблюдаться максимумы и минимумы амплитуды.

Максимум амплитуды будет определяться следующим условием.

(5)

m = 0, 1, 2…

x_max – координата максимальной амплитуды.

Косинус принимает максимальное значение по модулю через p.

Каждый из этих максимумов можно рассматривать как центр соответствующей группы волн.

Разрешив (5) относительно x_max получим.

Так как фазовая скорость , то называется групповой скоростью. С такой скоростью перемещается максимум амплитуды волнового пакета. В пределе, выражение для групповой скорости будет иметь следующий вид.

(6)

Это выражение справедливо для центра группы произвольного числа волн.

Следует отметить, что при точном учёте всех членов разложения (для произвольного числа волн), выражение для амплитуды получается таким, что из него следует, что волновой пакет со временем расплывается.
Выражению для групповой скорости можно придать другой вид.

, следовательно, выражение для групповой скорости можно записать следующим образом.

(7)

– неявное выражение, так как и v, и k зависят от длины волны l.

Тогда (8)

Подставим в (7) и получим.

(9)

Это так называемая формула Рэлея. Дж. У. Рэлей (1842 – 1919) английский физик, нобелевский лауреат 1904 года, за открытие аргона.

Из этой формулы следует, что в зависимости от знака производной групповая скорость может быть больше или меньше фазовой.

В отсутствии дисперсии

Максимум интенсивности приходится на центр группы волн. Поэтому скорость переноса энергии равна групповой скорости.

Понятие групповой скорости применимо только при условии, что поглощение волны в среде невелико. При значительном затухании волн понятие групповой скорости утрачивает смысл. Этот случай наблюдается в области аномальной дисперсии. Это мы будем рассматривать в разделе " Волновая оптика".

 

Колебания струны

 

В закреплённой с обоих концов натянутой струне при возбуждении поперечных колебаний устанавливаются стоячие волны, причём в местах закрепления струны располагаются узлы. Поэтому в струне возбуждаются с заметной интенсивностью только такие колебания, половина длины волны которых укладывается на длине струны целое число раз.

Отсюда вытекает следующее условие.

или

( n = 1, 2, 3, …),

l – длина струны. Длины волн соответствуют следующим частотам.

( n = 1, 2, 3, …).

Фазовая скорость волны определяется силой натяжения струны и массой единицы длины, т.е. линейной плотностью струны.

F – сила натяжения струны, ρ ' – линейная плотность материала струны. Частоты ν _n называются собственными частотами струны. Собственные частоты являются кратными частоте основного тона.

Эта частота называется основной частотой.

Гармонические колебания с такими частотами называются собственными или нормальными колебаниями. Их также называют гармониками. В общем случае колебание струны представляет собой наложение различных гармоник.

Колебания струны примечательны в том отношении, что для них по классическим представлениям получаются дискретные значения одной из характеризующих колебания величин (частоты). Для классической физики такая дискретность является исключением. Для квантовых процессов дискретность является скорее правилом, чем исключением.

Энергия упругой волны

Пусть в некоторой точке среды в направлении x распространяется плоская волна.

(1)

Выделим в среде элементарный объём Δ V, чтобы в пределах этого объёма скорость смещения частиц среды и деформация среды были постоянны.

Объём Δ V обладает кинетической энергией.

 

(2)

( ρ ·Δ V – масса этого объёма).

Этот объём обладает также и потенциальной энергией.

Для понимания вспомним.

Относительное смещение , α – коэффициент пропорциональности.

Модуль Юнга E = 1/α . Нормальное напряжение T = F/S. Отсюда.

В нашем случае .

В нашем случае имеем.

(3)

Вспомним также.

Тогда . Подставим в (3).

(4)

Для полной энергии получим.

 

Поделим на элементарный объём Δ V и получим объёмную плотность энергии волны.

(5)

Получим из (1) и .

(6)

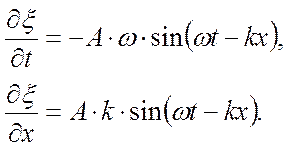
Подставим (6) в (5) и учтём, что . Получим.

(7)

Из (7) следует, что объёмная плотность энергии в каждый момент времени в разных точках пространства различна. В одной точке пространства W₀ изменяется по закону квадрата синуса. А среднее значение этой величины от периодической функции . Следовательно, средняя величина объёмной плотности энергии определится выражением.

(8)

Выражение (8) очень похоже на выражение для полной энергии колеблющегося тела . Следовательно, среда, в которой распространяется волна, обладает запасом энергии. Эта энергия передаётся от источника колебаний в разные точки среды.

Количество энергии, переносимое волной через некоторую поверхность в единицу времени, называется потоком энергии.

Если через данную поверхность за время dt переносится энергия dW, то поток энергии Ф будет равен.

(9)

– измеряется в ваттах.

Для характеристики течения энергии в разных точках пространства вводится векторная величина, которая называется плотностью потока энергии. Она численно равна потоку энергии через единичную площадку, размещённую в данной точке пространства перпендикулярно направлению переноса энергии. Направление вектора плотности потока энергии совпадает с направлением переноса энергии.

(10)

Эта характеристика энергии, переносимой волной, была введена русским физиком Н.А. Умовым (1846 – 1915) в 1874 году.

Рассмотрим поток энергии волны.

Поток энергии волны

Энергия волны

W₀ – это объёмная плотность энергии.

Тогда получим.

(11)

Так как волна распространяется в определённом направлении, то можно записать.

(12)

Это вектор плотности потока энергии или поток энергии через единичную площадку, перпендикулярную направлению распространения волны в единицу времени. Этот вектор называется вектором Умова.

~ sin²ω t.

Тогда среднее значение вектора Умова будет равно.

(13)

Интенсивность волны – среднее по времени значение плотности потока энергии, переносимой волной.

Очевидно.

(14)

Соответственно.

(15)

 

Звук

 

Звук – есть колебание упругой среды, воспринимаемые ухом человека.

Учение о звуке называется акустикой.

Физиологическое восприятие звука: громкий, тихий, высокий, низкий, приятный, противный – является отражением его физических характеристик. Гармоническое колебание определённой частоты воспринимается как музыкальный тон.

Частота звука соответствует высоте тона.

Ухо воспринимает диапазон частот от 16 Гц до 20000 Гц. При частотах меньше 16 Гц – инфразвук, а при частотах больше 20 кГц – ультразвук.

Несколько одновременных звуковых колебаний есть созвучие. Приятное - консонанс, неприятное – диссонанс. Большое число одновременно звучащих колебаний с разными частотами – шум.

Как мы уже знаем, под интенсивностью звука понимают среднее по времени значение плотности потока энергии, которую несёт с собой звуковая волна. Для того чтобы вызвать звуковое ощущение, волна должна обладать некоторой минимальной интенсивностью, которая называется порогом слышимости (кривая 1 на рисунке). Порог слышимости несколько различен для разных людей и сильно зависит от частоты звука. Наиболее чувствительно человеческое ухо к частотам от 1 кГц до 4 кГц. В этой области порог слышимости составляет в среднем 10^-12 Вт/м². При других частотах порог слышимости лежит выше.

При интенсивностях порядка 1 ÷ 10 Вт/м² волна перестаёт восприниматься как звук, вызывая в ухе лишь ощущение боли и давления. Значение интенсивности, при котором это происходит, называется порогом болевого ощущения (кривая 2 на рисунке). Порог болевого ощущения, так же как и порог слышимости, зависит от частоты.

Таким образом, лежит почти 13 порядков. Поэтому ухо человека не чувствительно к малым изменениям силы звука. Для ощущения изменения громкости интенсивность звуковой волны должна изменяться не менее чем на 10 ÷ 20%. Поэтому в качестве характеристики интенсивности выбирают не саму силу звука, а следующую величину, которая называется уровнем силы звука (или уровнем громкости) и измеряется в белах. В честь американского электротехника А.Г. Белла (1847 – 1922), одного из изобретателей телефона.

 

 

I₀ = 10^-12 Вт/м² – нулевой уровень (порог слышимости).

Т.е. 1 Б = 10· I₀.

Пользуются и в 10 раз более мелкой единицей – децибел (дБ).

 

 

С помощью этой формулы может быть выражено в децибелах уменьшение интенсивности (затухания) волны на некотором пути. Например, затухание в 20 дБ означает, что интенсивность волны уменьшается в 100 раз.

Весь диапазон интенсивностей, при которых волна вызывает в человеческом ухе звуковое ощущение (от 10^-12 до 10 Вт/м²), соответствует значениям громкости от 0 до 130 дБ.

 

Звук	Уровень громкости, дБ
Тиканье часов
Шепот на расстоянии 1 м
Тихий разговор
Речь средней громкости
Громкая речь
Крик
Шум реактивного самолета на расстоянии 5 м
Шум реактивного самолета на расстоянии 3 м

Энергия, которую несут с собой звуковые волны, крайне мала. Например, чтобы нагреть стакан с водой от комнатной температуры до кипения звуковой волной с уровнем громкости 70 дБ (в этом случае в секунду водой будет поглощаться примерно 2·10^-7 Вт) потребуется время порядка десяти тысяч лет.

Ультразвуковые волны могут быть получены в виде направленных пучков, подобно пучкам света. Направленные ультразвуковые пучки нашли широкое применение в гидролокации. Идея была выдвинута французским физиком П. Ланжевеном (1872 – 1946) во время первой мировой войны (в 1916 году). Кстати, метод ультразвуковой локации позволяет летучей мыши хорошо ориентироваться при полёте в темноте.

 

Волновое уравнение

 

В области волновых процессов существуют уравнения, называемые волновыми , которые описывают все возможные волны, независимо от их конкретного вида. По смыслу волновое уравнение подобно основному уравнению динамики, которое описывает все возможные движения материальной точки. Уравнение любой конкретной волны является решением волнового уравнения. Получим его. Для этого продифференцируем дважды по t и по всем координатам уравнение плоской волны .

(1)

Отсюда получим.

(*)

Сложим уравнения (2).

(3)

Заменим x в (3) из уравнения (*). Получим.

Учтём, что и получим.

, или . (4)

Это и есть волновое уравнение. В этом уравнении – фазовая скорость, – оператор набла или оператор Лапласа.

Всякая функция, удовлетворяющая уравнению (4), описывает некоторую волну, причём корень квадратный из величины, обратной коэффициенту при второй производной смещения от времени, даёт фазовую скорость волны.

Легко убедиться, что волновому уравнению удовлетворяют уравнения плоской и сферической волн, а также любое уравнение вида

Для плоской волны, распространяющейся в направлении , волновое уравнение имеет вид:

.

Это одномерное волновое уравнение второго порядка в частных производных, справедливое для однородных изотропных сред с пренебрежимо малым затуханием.

 

Электромагнитные волны

Рассматривая уравнения Максвелла, мы записали важный вывод о том, что переменное электрическое поле порождает магнитное, которое тоже оказывается переменным. В свою очередь переменное магнитное поле порождает переменное электрическое поле и т.д. Электромагнитное поле способно существовать самостоятельно – без электрических зарядов и токов. Изменение состояния этого поля имеет волновой характер. Поля такого рода называют электромагнитными волнами. Существование электромагнитных волн вытекает из уравнений Максвелла.

Рассмотрим однородную нейтральную ( ) непроводящую ( ) среду, например, для простоты, вакуум. Для этой среды можно записать:

, .

Если рассматривается любая иная однородная нейтральная непроводящая среда, то в записанные выше уравнения нужно добавить и .

Запишем дифференциальные уравнения Максвелла в общем виде.

, , , .

Для рассматриваемой среды эти уравнения имеют вид:

, , ,

Запишем эти уравнения следующим образом:

, , , .

Любые волновые процессы должны описываться волновым уравнением, которое связывает вторые производные по времени и координатам. Из записанных выше уравнений путем несложных преобразований можно получить следующую пару уравнений:

,

Эти соотношения представляют собой идентичные волновые уравнения для полей и .

Вспомним, что в волновом уравнении ( ) множитель перед второй производной в правой части – это величина, обратная квадрату фазовой скорости волны. Следовательно, . Оказалось, что в вакууме эта скорость для электромагнитной волны равна скорости света.

Тогда волновые уравнения для полей и можно записать как

и .

Эти уравнения указывают на то, что электромагнитные поля могут существовать в виде электромагнитных волн, фазовая скорость которых в вакууме равна скорости света.

Математический анализ уравнений Максвелла позволяет сделать вывод о структуре электромагнитной волны, распространяющейся в однородной нейтральной непроводящей среде при отсутствии токов и свободных зарядов. В частности, можно сделать вывод о векторной структуре волны. Электромагнитная волна является строго поперечной волной в том смысле, что характеризующие ее векторы и перпендикулярны к вектору скорости волны , т.е. к направлению ее распространения. Векторы , и , в том порядке, в котором они записаны, образуют правовинтовую ортогональную тройку векторов. В природе существуют только правовинтовые электромагнитные волны, и не существует левовинтовых волн. В этом состоит одно из проявлений законов взаимного создания переменных магнитных и электрических полей.

Из уравнений Максвелла следует также, что в электромагнитной волне векторы и всегда колеблются в одинаковых фазах, а мгновенные значения и в любой точке пространства связаны соотношением .

Рассмотрим для простоты вид и свойства одномерного волнового уравнения электромагнитной волны в однородной нейтральной непроводящей среде. Пусть электромагнитная волна будет строго монохроматической (волны и имеют одну и ту же частоту) и распространяется в направлении . Векторы и перпендикулярны направлению распространения волны, следовательно, их проекции на ось равны нулю. Волновые уравнения такой волны будут иметь вид:

,

Этим уравнениям удовлетворяют плоские линейно поляризованные монохроматические волны

,

Мгновенная картина электромагнитной волны в некоторый момент времени изображена на рисунке.

Индексы и означают, что векторы и направлены вдоль взаимно перпендикулярных осей и . и соответственно амплитуды напряженностей электрического и магнитного полей волны; - частота волны;

– волновое число; - начальные фазы колебаний в точках с координатой (колебания электрического и магнитного векторов в электромагнитной волне происходят в одной фазе, так что в обоих уравнениях одинаково).

 

Оптический эффект Доплера

 

В акустике изменение частоты, обуславливающее эффект Доплера, определяется скоростями движения приёмника и источника относительно среды, являющейся носителем звуковых волн. Скорость звука определяется свойствами среды, а не скоростью источника.

Для световых волн также существует эффект Доплера, но здесь нет среды носителя электромагнитных волн. Доплеровское изменение частоты световых волн определяется только относительной скоростью источника и приёмника. Существует два оптических эффекта Доплера: продольный и поперечный. Рассмотрим продольный эффект Доплера.

Источник находится в системе K, а приёмник – в системе K'. Приёмник K' движется относительно источника K со скоростью v в направлении x.

Запишем уравнение плоской световой (электромагнитной) волны в системе K.

(1)

w – частота колебаний источника (предполагается, что свет распространяется в вакууме, т.е. с фазовой скоростью, равной c ).

Согласно принципу относительности законы природы имеют одинаковый вид во всех инерциальных системах отсчёта. Следовательно, в системе K' волна будет описываться следующим уравнением.

(2)

w' – частота воспринимаемая приёмником.

Легко поставить штрихи, а необходимо найти связь между уравнениями.

От (1) к (2) можно перейти, воспользовавшись преобразованиями Лоренца.

(3)

Уравнение (3) описывает в системе K' ту же волну, что и уравнение (2). Поэтому можно записать.

Итак, если источник и приёмник удаляются друг от друга, то получается.

или (4)

Если источник и приёмник движутся навстречу друг другу, то числитель и знаменатель меняются местами.

или (4')

При удалении приёмника от источника v > 0, следовательно, n' < n. При приближении – v < 0, следовательно, n' > n.

При v < < c формулы (4) можно приближённо записать.

или

 

Отсюда относительное изменение частоты будет равно.

Для световых волн кроме продольного эффекта Доплера существует поперечный эффект Доплера. Он заключается в изменении частоты, воспринимаемой приёмником, когда вектор относительной скорости v направлен перпендикулярно прямой соединяющей источник и приёмник. Например, источник движется по окружности, а приёмник находится в её центре. Относительное изменение частоты в этом случае определяется следующим выражением.

Поперечный эффект Доплера пропорционален и, следовательно, меньше продольного эффекта Доплера.

В общем случае вектор относительной скорости v можно разложить на две составляющие: продольную и поперечную.

Продольный эффект Доплера для электромагнитных волн широко используется в радиолокации, для определения скорости воздушных целей. В астрономии – для определения радиальной скорости звёзд.

Тепловое, колебательное движение атомов и молекул приводит к уширению спектральных линий при излучении и поглощении. В результате их излучения будут наблюдаться все частоты, лежащие в интервале от до

1234567Следующая ⇒

Поделиться: