Распространение волн в газах

 

Волна в газе представляет собой распространяющуюся в пространстве последовательность чередующихся областей сжатия и разряжения газа. Следовательно, давление в каждой точке пространства испытывает периодически изменяющееся отклонение Δ P от среднего значения P, совпадающего с давлением, которое существует в газе в отсутствие волн. Т.о., мгновенное значение давления в некоторой точке пространства можно представить в следующем виде.

Причём

Пусть волна распространяется вдоль оси x. Рассмотрим объём газа в цилиндре с площадью основания S и высотой Δ x (см. рис.). Масса газа, заключённая в этом объёме равна ρ ·S·Δ x, где ρ – плотность невозмущённого волной газа. В виду малости Δ x проекцию ускорения на ось x для всех точек цилиндра можно считать одинаковой и равной .

Проекция силы на ось x равна.

Будем иметь в виду, что Δ ξ < < Δ x.

Запишем для этого объёма газа уравнение второго закона Ньютона.

Сократим на S·Δ x и получим.

(1)

В полученном нами дифференциальном уравнении содержится две неизвестные функции: ξ и P'. Выразим одну из этих функций через другую. Для этого найдём связь между давлением газа P' и относительным изменением его объёма . Эта связь зависит от характера сжатия (или расширения) газа. В акустической волне сжатия и расширения газа следуют друг за другом так часто, что смежные участки среды не успевают обмениваться теплом, и процесс можно считать адиабатическим. При адиабатическом процессе связь между давлением и объёмом даётся следующим уравнением.

(2)

γ – отношение теплоёмкости газа при постоянном давлении к теплоёмкости при постоянном объёме. Тогда в соответствии с (2) можно записать.

Сократим на (S·Δ x)^γ и получим.

Воспользуемся тем, что по предположению , разложим выражение в скобках в ряд по степеням и пренебрежём членами высших порядков малости. В результате получим.

Решим это уравнение относительно P'.

(3)

(Мы воспользовались формулой , справедливой для x < < 1). Из найденного нами соотношения легко получить выражение для Δ P.

(4)

Поскольку γ – величина порядка единицы, то из (4) вытекает, что . Таким образом, условие означает, что отклонение давления от среднего значения много меньше самого давления. Это действительно так: для самых громких звуков амплитуда колебаний давления воздуха не превышает 1 мм рт. ст., в то время как атмосферное давление P имеет величину порядка 10³ мм рт. ст.

Продифференцируем (3) по x и получим.

Подставим это значение в формулу (1), получим некоторое дифференциальное уравнение.

Это волновое уравнение. Мы его рассмотрим несколько позже. Величина обратная выражению перед второй производной по времени даёт фазовую скорость звуковых волн в газе. Тогда имеем.

(5)

(Напомним, что P и ρ – давление и плотность невозмущенного волной газа).

При атмосферном давлении и обычных температурах большинство газов по своим свойствам близки к идеальному газу. Поэтому из уравнения Менделеева-Клапейрона отношение . (здесь R – газовая постоянная; T – термодинамическая температура; μ – масса одного моля газа). Подставим это значение в (5) и получим формулу для скорости звука в газе.

(6)

Из этой формулы следует, что скорость звука пропорциональна корню квадратному из температуры и не зависит от давления.

Вычислим значение скорости звука в воздухе при комнатной температуре ( T = 290 К). Для воздуха γ = 1, 4, μ = 29·10^-3 кг/моль. Газовая постоянная равна 8, 31 Дж/(моль·К). Подставим эти значения в формулу (6) и получим.

Найденное нами значение скорости звука в воздухе хорошо согласуется со значением, полученным опытным путём.

Скорость звука в жидкости.

, где - объемный модуль упругости жидкости, – её плотность.

 

 

Энергия упругой волны

Пусть в некоторой точке среды в направлении x распространяется плоская волна.

(1)

Выделим в среде элементарный объём Δ V, чтобы в пределах этого объёма скорость смещения частиц среды и деформация среды были постоянны.

Объём Δ V обладает кинетической энергией.

 

(2)

( ρ ·Δ V – масса этого объёма).

Этот объём обладает также и потенциальной энергией.

Для понимания вспомним.

Относительное смещение , α – коэффициент пропорциональности.

Модуль Юнга E = 1/α . Нормальное напряжение T = F/S. Отсюда.

В нашем случае .

В нашем случае имеем.

(3)

Вспомним также.

Тогда . Подставим в (3).

(4)

Для полной энергии получим.

 

Поделим на элементарный объём Δ V и получим объёмную плотность энергии волны.

(5)

Получим из (1) и .

(6)

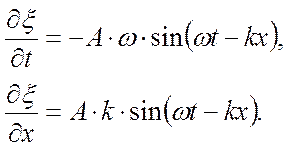
Подставим (6) в (5) и учтём, что . Получим.

(7)

Из (7) следует, что объёмная плотность энергии в каждый момент времени в разных точках пространства различна. В одной точке пространства W₀ изменяется по закону квадрата синуса. А среднее значение этой величины от периодической функции . Следовательно, средняя величина объёмной плотности энергии определится выражением.

(8)

Выражение (8) очень похоже на выражение для полной энергии колеблющегося тела . Следовательно, среда, в которой распространяется волна, обладает запасом энергии. Эта энергия передаётся от источника колебаний в разные точки среды.

Количество энергии, переносимое волной через некоторую поверхность в единицу времени, называется потоком энергии.

Если через данную поверхность за время dt переносится энергия dW, то поток энергии Ф будет равен.

(9)

– измеряется в ваттах.

Для характеристики течения энергии в разных точках пространства вводится векторная величина, которая называется плотностью потока энергии. Она численно равна потоку энергии через единичную площадку, размещённую в данной точке пространства перпендикулярно направлению переноса энергии. Направление вектора плотности потока энергии совпадает с направлением переноса энергии.

(10)

Эта характеристика энергии, переносимой волной, была введена русским физиком Н.А. Умовым (1846 – 1915) в 1874 году.

Рассмотрим поток энергии волны.

Поток энергии волны

Энергия волны

W₀ – это объёмная плотность энергии.

Тогда получим.

(11)

Так как волна распространяется в определённом направлении, то можно записать.

(12)

Это вектор плотности потока энергии или поток энергии через единичную площадку, перпендикулярную направлению распространения волны в единицу времени. Этот вектор называется вектором Умова.

~ sin²ω t.

Тогда среднее значение вектора Умова будет равно.

(13)

Интенсивность волны – среднее по времени значение плотности потока энергии, переносимой волной.

Очевидно.

(14)

Соответственно.

(15)

 

Звук

 

Звук – есть колебание упругой среды, воспринимаемые ухом человека.

Учение о звуке называется акустикой.

Физиологическое восприятие звука: громкий, тихий, высокий, низкий, приятный, противный – является отражением его физических характеристик. Гармоническое колебание определённой частоты воспринимается как музыкальный тон.

Частота звука соответствует высоте тона.

Ухо воспринимает диапазон частот от 16 Гц до 20000 Гц. При частотах меньше 16 Гц – инфразвук, а при частотах больше 20 кГц – ультразвук.

Несколько одновременных звуковых колебаний есть созвучие. Приятное - консонанс, неприятное – диссонанс. Большое число одновременно звучащих колебаний с разными частотами – шум.

Как мы уже знаем, под интенсивностью звука понимают среднее по времени значение плотности потока энергии, которую несёт с собой звуковая волна. Для того чтобы вызвать звуковое ощущение, волна должна обладать некоторой минимальной интенсивностью, которая называется порогом слышимости (кривая 1 на рисунке). Порог слышимости несколько различен для разных людей и сильно зависит от частоты звука. Наиболее чувствительно человеческое ухо к частотам от 1 кГц до 4 кГц. В этой области порог слышимости составляет в среднем 10^-12 Вт/м². При других частотах порог слышимости лежит выше.

При интенсивностях порядка 1 ÷ 10 Вт/м² волна перестаёт восприниматься как звук, вызывая в ухе лишь ощущение боли и давления. Значение интенсивности, при котором это происходит, называется порогом болевого ощущения (кривая 2 на рисунке). Порог болевого ощущения, так же как и порог слышимости, зависит от частоты.

Таким образом, лежит почти 13 порядков. Поэтому ухо человека не чувствительно к малым изменениям силы звука. Для ощущения изменения громкости интенсивность звуковой волны должна изменяться не менее чем на 10 ÷ 20%. Поэтому в качестве характеристики интенсивности выбирают не саму силу звука, а следующую величину, которая называется уровнем силы звука (или уровнем громкости) и измеряется в белах. В честь американского электротехника А.Г. Белла (1847 – 1922), одного из изобретателей телефона.

 

 

I₀ = 10^-12 Вт/м² – нулевой уровень (порог слышимости).

Т.е. 1 Б = 10· I₀.

Пользуются и в 10 раз более мелкой единицей – децибел (дБ).

 

 

С помощью этой формулы может быть выражено в децибелах уменьшение интенсивности (затухания) волны на некотором пути. Например, затухание в 20 дБ означает, что интенсивность волны уменьшается в 100 раз.

Весь диапазон интенсивностей, при которых волна вызывает в человеческом ухе звуковое ощущение (от 10^-12 до 10 Вт/м²), соответствует значениям громкости от 0 до 130 дБ.

 

Звук	Уровень громкости, дБ
Тиканье часов
Шепот на расстоянии 1 м
Тихий разговор
Речь средней громкости
Громкая речь
Крик
Шум реактивного самолета на расстоянии 5 м
Шум реактивного самолета на расстоянии 3 м

Энергия, которую несут с собой звуковые волны, крайне мала. Например, чтобы нагреть стакан с водой от комнатной температуры до кипения звуковой волной с уровнем громкости 70 дБ (в этом случае в секунду водой будет поглощаться примерно 2·10^-7 Вт) потребуется время порядка десяти тысяч лет.

Ультразвуковые волны могут быть получены в виде направленных пучков, подобно пучкам света. Направленные ультразвуковые пучки нашли широкое применение в гидролокации. Идея была выдвинута французским физиком П. Ланжевеном (1872 – 1946) во время первой мировой войны (в 1916 году). Кстати, метод ультразвуковой локации позволяет летучей мыши хорошо ориентироваться при полёте в темноте.

 

⇐ Предыдущая1234567Следующая ⇒

Поделиться: